Questão 1
Considerando os polinômios p(x) = x³ + 5x² – 10 e q(x) = – x² + 6x + 4, o valor de p(2) : q(1) é:
A) 2
B) 5
C) 9
D) 15
E) 18
Questão 2
Analisando o polinômio 4x5 + 8x³ – x, podemos afirmar que o grau desse polinômio é igual a:
A) 4
B) 5
C) 8
D) 10
E) 12
Questão 3
Considere o polinômio P(x) = x³ + 2x² – 5x – 3. O valor da expressão |2 · P(1)| é:
A) 5
B) – 5
C) 0
D) – 10
E) 10
Questão 4
(Instituto Consulplan) Se R(x) é o resto da divisão do polinômio P(x) = x4 – 3x3 + 2x – 3 pelo polinômio D(x) = x + 1, então o valor de R(x) é:
A)
B) 1
C) – 1
D) – 2
Questão 5
Considerando que – 3 é uma das raízes do polinômio p(x) = 2x³ – 4kx + 24, então o valor de k é:
A) 1,0
B) 1,5
C) 2,0
D) 2,5
E) 3,0
Questão 6
(Imparh) Temos uma caixa no formato de um paralelepípedo retorretângulo com profundidade x − 1, comprimento x + 1 e largura x (em que x ≥ 1 é um número real). Qual polinômio expressa o volume, V(x), dessa caixa?
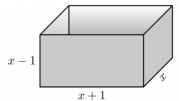
A) V(x) = x² − 1
B) V(x) = x³ − 1
C) V(x) = x³ − x
D) V(x) = x³ + 2x² +x
Questão 7
Qual deve ser o valor de k para que o polinômio P(x) = (k² – 81)x5 + (k – 9)x4 + kx³ + 3x² – 4x tenha grau 3?
A) – 1
B) 3
C) – 3
D) ± 9
E) 9
Questão 8
O polinômio que representa o perímetro do trapézio a seguir é:
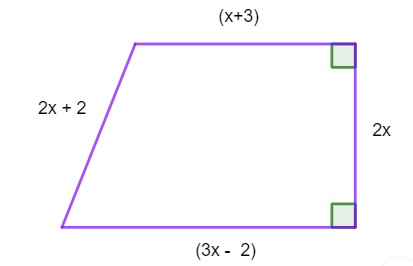
A) 8x + 3
B) 11x
C) 4x² + 2
D) x² + 11
E) 11x – 3
Questão 9
Considerando os polinômios a seguir:
-
X = 2x³ + 4x² + 2y² + 4
-
Y = – 7x² + y² + 2
-
Z = x³ – 2x² + y² + 3
O valor da soma X + Y – 2Z é igual a:
A) y² + 2x² + 2
B) 2x³
C) 2x³ + x² + y² – 3
D) x² + 4y² + 3
E) x² + y²
Questão 10
Analise as afirmativas a seguir:
I → O grau de um polinômio é dado pelo maior coeficiente de suas variáveis.
II → O valor numérico de P(x) = 3x² – 4x + 2 quando x = 2 é 6.
III → O polinômio p(x) = 4x³ + 2x² – 1 possui grau 4.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas I e II são verdadeiras.
E) Todas as afirmativas são verdadeiras.
Questão 11
O perímetro do polígono a seguir pode ser expresso pelo seguinte polinômio:
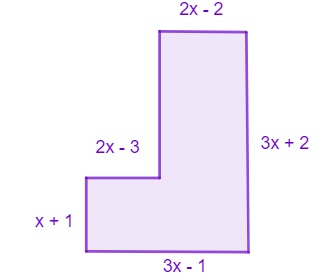
A) 2x – 1
B) 8x + 4
C) 11x – 3
D) 10x + 4
E) x³ + 3
Questão 12
(Enem 2012) Um forro retangular de tecido traz em sua etiqueta a informação de que encolherá após a primeira lavagem mantendo, entretanto, seu formato. A figura a seguir mostra as medidas originais do forro e o tamanho do encolhimento (x) no comprimento e (y) na largura. A expressão algébrica que representa a área do forro após ser lavado é (5 – x) (3 – y).
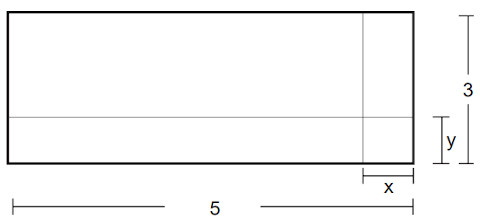
Nessas condições, a área perdida do forro, após a primeira lavagem, será expressa por
A) 2xy
B) 15 − 3x
C) 15 − 5y
D) −5y − 3x
E) 5y + 3x − xy
Resposta Questão 1
Alternativa A
Calculando p(2):
p(2) = 2³ + 5 · 2² – 10
p(2) = 8 + 5 · 4 – 10
p(2) = 8 + 20 – 10
p(2) = 28 – 10
p(2) = 18
Calculando q(1):
q(1) = – 1² + 6 ⸳ 1 + 4
q(1) = – 1 + 6 + 4
q(1) = 9
A divisão entre p(2) e q(1) é então = 18 : 9 = 2.
Resposta Questão 2
Alternativa B
O grau do polinômio é o maior expoente da sua variável, que, nesse caso, é igual a 5.
Resposta Questão 3
Alternativa E
Calculando P(1):
P(1) = 1³ + 2 ⸳ 1² – 5 · 1 – 3
P(1) = 1 + 2 – 5 – 3
P(1) = – 5
Então, |2 P(1)| = |2 · (– 5)| = |– 10| = 10
Resposta Questão 4
Alternativa C
Para encontrar o resto da divisão de P(x) por D(x), aplicaremos o teorema do resto de um polinômio, pois temos que:
D(x) = x + 1
x + 1 = 0
x = – 1
Agora, calculando P(– 1):
P(– 1) = (– 1)4 – 3(– 1)3 + 2(– 1) – 3
P(– 1) = 1 + 3 – 2 – 3
P(– 1) = – 1
Resposta Questão 5
Alternativa D
Sabendo que – 3 é raiz dessa equação, então temos que:
p(– 3) = 2 (– 3)³ – 4 (– 3)k + 24
0 = 2 (– 27) + 12k + 24
0 = – 54 + 12k + 24
– 12k = – 54 + 24
– 12k = – 30
k = (– 30) : (– 12)
k = 2,5
Resposta Questão 6
Alternativa C
Para encontrar o volume, multiplicamos as três dimensões:
V(x) = (x – 1) ( x + 1)x
V(x) = (x² – x + x – 1²)x
V(x) = (x² – 1)x
V(x) = x³ – x
Resposta Questão 7
Alternativa E
Para que o polinômio seja de grau 3, temos que:
k – 9 = 0 e k² – 81 = 0.
Resolvendo a primeira equação, temos que:
k – 9 = 0
k = 9
Note que k = 9 também é solução da segunda equação, pois
9² – 81 = 0
81 – 81 = 0
0 = 0
Então, o único valor que faz com que esse polinômio seja de grau 3 é k = 9.
Resposta Questão 8
Resposta Questão 9
Alternativa E
Realizando a soma, temos que:
(2x³ + 4x² + 2y² + 4) + (– 7x² + y² + 2) – 2(x³ – 2x² + y² + 3)
2x³ + 4x² + 2y² + 4 – 7x² + y² + 2 – 2x³ + 4x² – 2y² – 6
Juntando os termos semelhantes, encontraremos:
x² + y²
Resposta Questão 10
Alternativa B
-
I → Falsa. O que define o grau de um polinômio é seu expoente, e não seu coeficiente.
-
II → Verdadeira. Calculando:
P(2) = 3 · 2² – 4 ⸳ 2 + 2
P(2) = 3 · 4 – 8 + 2
P(2) = 12 – 8 + 2
P(2) = 6
-
III → Falsa. O grau do polinômio é 3.
Resposta Questão 11
Alternativa C
Calculando o perímetro, temos que:
P = 2x – 3 + x + 1 + 3x – 1 + 3x + 2 + 2x – 2
P = 11x – 3
Resposta Questão 12
Alternativa E
A área perdida pode ser separada em três retângulos.
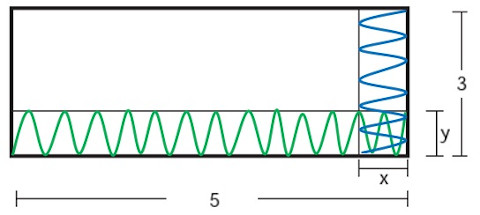
O primeiro retângulo, destacado em verde, tem área 5y, e o segundo retângulo, destacado em azul, tem área 3x. Note, porém, que existe uma região em comum tanto para o retângulo verde quanto para o retângulo azul, de área xy, que está sendo contada tanto na área do primeiro retângulo quanto na do segundo retângulo.
Por isso, a área perdida vai ser a soma da área do retângulo em verde com o retângulo em azul menos a área em comum.
5y + 3x – xy



