Questão 1
Uma pirâmide possui base retangular com lados da base medindo 7 cm e 6 cm. Se a altura dessa pirâmide for de 8 cm, então o seu volume será:
A) 84 cm³
B) 96 cm³
C) 108 cm³
D) 112 cm³
E) 192 cm³
Questão 2
Uma pirâmide retangular de base quadrada possui volume igual a 375 cm³ e altura igual a 10 cm. A medida da área da base dessa pirâmide é igual a:
A) 79,4 cm²
B) 85,6 cm²
C) 96,8 cm²
D) 112,5 cm²
E) 150,0 cm²
Questão 3
Uma pirâmide possui base quadrada, com altura medindo 16 cm e comprimento da aresta da base igual a 24 cm, então o apótema dessa pirâmide é igual a:
A) 18 cm
B) 20 cm
C) 25 cm
D) 28 cm
E) 30 cm
Questão 4
Qual é o número de arestas que uma pirâmide de base hexagonal possui?
A) 6
B) 7
C) 8
D) 10
E) 12
Questão 5
Analise a pirâmide a seguir:

Sabendo que a sua base é um hexágono regular, o volume dessa pirâmide é igual a: (Use \(\sqrt3=1,7\).)
A) 574 cm²
B) 816 cm³
C) 1632 cm³
D) 2448 cm³
E) 4896 cm³
Questão 6
Uma pirâmide possui base retangular com lados medindo 8 cm e 12 cm. Sabendo que o seu volume é de 576 cm³, então a medida da altura dessa pirâmide é:
A) 14 cm
B) 15 cm
C) 16 cm
D) 17 cm
E) 18 cm
Questão 7
Analise a pirâmide a seguir:

Sabendo que a sua base é quadrada, então a sua área total é:
A) 144 cm²
B) 240 cm²
C) 264 cm²
D) 384 cm²
E) 420 cm²
Questão 8
Analise as planificações a seguir:

Essas planificações são, respectivamente, de:
A) prisma triangular, prisma quadrado e prisma pentagonal.
B) tetraedro, cubo e pirâmide hexagonal.
C) octaedro, prisma de base quadrada e pirâmide pentagonal.
D) pirâmide triangular, pirâmide quadrada e pirâmide pentagonal.
E) tetraedro, pentaedro e hexaedro.
Questão 9
(Fuvest) Um telhado tem a forma da superfície lateral de uma pirâmide regular, de base quadrada. O lado da base mede 8 m, e a altura da pirâmide, 3 m. As telhas para cobrir esse telhado são vendidas em lotes que cobrem 1 m². Supondo que possa haver 10 lotes de telhas desperdiçadas (quebras e emendas), o número mínimo de lotes de telhas a ser comprado é:
A) 90
B) 100
C) 110
D) 120
E) 130
Questão 10
(Unirio)

Uma pirâmide está inscrita em um cubo, como mostra a figura anterior. Sabendo-se que o volume da pirâmide é de 6 m³, então o volume do cubo, em m³, é igual a:
A) 9
B) 12
C) 15
D) 18
E) 21
Questão 11
(UFF) A grande pirâmide de Quéops, antiga construção localizada no Egito, é uma pirâmide regular de base quadrada, com 137 m de altura. Cada face dessa pirâmide é um triângulo isósceles cuja altura relativa à base mede 179 m. A área da base dessa pirâmide, em m², é
A) 13.272
B) 53.088
C) 26.544
D) 79.432
E) 39.816
Questão 12
(Fundatec) Uma doceira optou por produzir docinhos de chocolate em formato de pirâmide regular de base quadrada. Sabendo que o lado da base mede 4 cm e a altura da pirâmide mede 4,5 cm, calcule quantos cm³ de chocolate são necessários para produzir 5 docinhos.
A) 82.
B) 90.
C) 105.
D) 120.
E) 132.
Resposta Questão 1
Alternativa D
Como a base da pirâmide é um retângulo, então a área da base é a multiplicação das duas dimensões:
\(A_b=7\cdot6=42\ cm²\)
Calculando o volume, temos que:
\(V=\frac{A_b\cdot h}{3}\)
\(V=\frac{42\cdot8}{3}\)
\(V=14\cdot8\)
\(V=112\ cm^3\)
Resposta Questão 2
Alternativa D
Sabemos que V = 375:
\(V=\frac{A_b\cdot h}{3}\)
\(375=\frac{A_b\cdot10}{3}\)
\(375\cdot3=A_b\cdot10\)
\(1125=10A_b\)
\(\frac{1125}{10}=A_b\)
\(112,5=A_b\)
Resposta Questão 3
Alternativa B
Para encontrar o apótema da pirâmide a, primeiramente vamos dividir o comprimento da aresta da base por 2 a fim de descobrir o apótema da base da pirâmide:
24 : 2 = 12
Aplicando o teorema de Pitágoras, temos que:
a² = 12² + 16²
a² = 144 + 256
a² = 400
a² = \(\sqrt{400}\)
a² = 20
A altura da face da pirâmide é de 20 cm.
Resposta Questão 4
Alternativa E
Primeiramente, faremos a ilustração de uma pirâmide de base hexagonal:
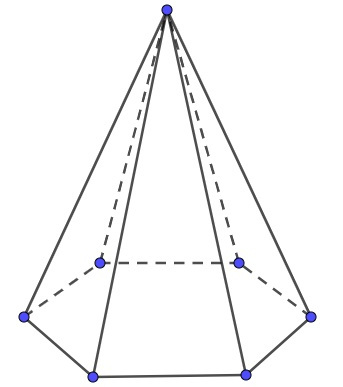
Analisando a imagem, podemos observar que há 6 arestas na base e 6 arestas laterais, logo há um total de 12 arestas.
Resposta Questão 5
Alternativa B
Como a base da pirâmide é um hexágono, a área do hexágono é:
\(A_b=6\cdot\frac{l^2\sqrt3}{4}\)
\(A_b=6\cdot\frac{8^2\cdot1,7}{4}\)
\(A_b=6\cdot\frac{64\cdot1,7}{4}\)
\(A_b=\frac{652,8}{4}\)
\(A_b=163,2\)
Sabendo a área da base, é possível calcular o volume dessa pirâmide:
\(V=\frac{A_b\cdot h}{3}\)
\(V=\frac{163,2\cdot15}{3}\)
\(V=163,2\ \cdot5\ \)
\(V=816\ cm^3\)
Resposta Questão 6
Alternativa E
Sabemos que a área da base dessa pirâmide é igual a:
\(A_b=8\cdot12=96\)
Utilizando a fórmula do volume, é possível encontrar a altura:
\(V=\frac{A_b\cdot h}{3}\)
\(576=\frac{96\cdot h}{3}\)
\(576=32h\)
\(h=\frac{576}{32}\)
\(h=18\ cm\)
Resposta Questão 7
Alternativa D
Para calcular a área total, é necessário calcular o apótema da face g desse triângulo. Para tanto, calcularemos a metade da aresta da base:
12 : 2 = 6
Sabemos que:
g² = 6² + 8²
g² = 36 + 64
g² = 100
g = \(\sqrt{100}\)
g = 10
Sabendo que g = 10, calcularemos a área do triângulo que forma a face lateral da pirâmide e multiplicaremos por 4 para encontrar a área lateral:
\(A_l=4\cdot\frac{b\cdot h}{2}\)
\(A_l=4\cdot\frac{12\cdot10}{2}\)
\(A_l=4\cdot6\cdot10\)
\(A_l=240\ cm^2\)
Agora, a área da base da pirâmide é igual à área do quadrado:
\(A_b=l^2\)
\(A_b={12}^2\)
\(A_b=144\ cm^2\)
A área total dessa pirâmide é de 144 + 240 = 384 cm².
Resposta Questão 8
Alternativa D
Note que as imagens possuem, respectivamente, uma face triangular, uma face quadrada e uma face pentagonal. As demais faces se encontram em um único ponto, que é o vértice da pirâmide, e são todas triangulares. Logo, temos as planificações de uma pirâmide triangular, uma pirâmide quadrada e uma pirâmide pentagonal.
Resposta Questão 9
Alternativa A
Queremos calcular a área lateral da pirâmide, assim encontraremos a medida do apótema da pirâmide e do apótema da base da pirâmide.
O apótema da base \(a_b\) é a metade da medida da aresta da base. Como ela mede 8 m:
\(a_b=8∶2=4\)
Agora, calcularemos o apótema da pirâmide a:
\(a^2=a_b^2+h^2\)
\(a^2=4^2+3^2\)
\(a^2=16+9\)
\(a^2=25\)
\(a=\sqrt{25}\)
\(a=5\)
Sabemos que a altura do triângulo da lateral é 5 e que a base desse triângulo mede 8. Como temos 4 triângulos na área lateral:
\(A_l=4\cdot\frac{8\cdot5}{2}\)
\(A_l=4\cdot4\cdot5\)
\(A_l=80\)
Para encontrar o número mínimo de lotes de telha, resta somar os 10 lotes desperdiçados:
80 + 10 = 90 lotes de telhas
Resposta Questão 10
Alternativa D
O volume de uma pirâmide que possui a mesma base e a mesma altura que o cubo é sempre igual a 1/3 do volume do cubo. Sendo assim, o volume do cubo é 3 vezes o volume da pirâmide. Como o volume da pirâmide é 6, então o volume do cubo é
6 ⋅ 3 = 18 m³
Resposta Questão 11
Alternativa B
Como a base é um quadrado, sendo a a aresta da base, a área da base é igual a \(a^2\). Sabemos que existe uma relação pitagórica entre a altura da pirâmide, a metade da aresta da base (conhecida como apótema da base) e a altura da face:
\({a_f}^2=h^2+\left(\frac{a}{2}\right)^2\)
\({179}^2={137}^2+\frac{a^2}{4}\)
\(32041=18769+\frac{a^2}{4}\)
\(32041-18769=\frac{a^2}{4}\)
\(13272\ =\ \frac{a^2}{4}\)
\(4\cdot13272=a^2\)
\(53088=a^2\)
Como a base é um quadrado, sabemos que a sua área é 53.088 m².
Resposta Questão 12
Alternativa D
Calculando o volume de um docinho, temos que:
\(V=\frac{A_b\cdot h}{3}\)
\(V=\frac{4^2\cdot4,5}{3}\)
\(V=16\cdot1,5\ \)
\(V=24\ cm^3\)
Se um docinho possui 24 cm³, então 5 terão \(24\cdot5=120\ cm^3\).



