Questão 1
Um sólido geométrico é conhecido como paralelepípedo quando ele possui todas as faces formadas por paralelogramos. Esse sólido é bastante presente no nosso cotidiano, como no formato de caixas, de tijolos, entre outros objetos. Sobre o paralelepípedo, podemos afirmar que o número de arestas, vértices e faces é, respectivamente:
A) 18, 12, 4
B) 14, 12, 8
C) 12, 10, 8
D) 12, 8, 6
E) 10, 8, 6
Questão 2
As embalagens de presente de uma loja possuem formato de paralelepípedo reto, com as medidas a seguir:
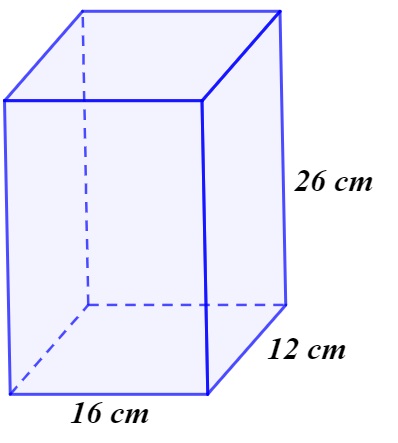
O volume dessa embalagem é de:
A) 4024 cm³
B) 4222 cm³
C) 4326 cm³
D) 4612 cm³
E) 4992 cm³
Questão 3
Para presentear a sua namorada, Armandinho decidiu comprar um perfume que vem em uma embalagem que possui formato de paralelepípedo reto com 12 cm de altura, 3,5 cm de largura e 8,5 cm de comprimento. Caso Armandinho decida embrulhar esse presente com papel de embrulho, a área do papel deve ser no mínimo igual a:
A) 347,5 cm²
B) 350,0 cm²
C) 354,5 cm²
D) 361,5 cm²
E) 369,0 cm²
Questão 4
Qual é a medida da diagonal de um paralelepípedo reto, com 1,6 metros de largura, 1,8 metros de altura e 2,4 metros de comprimento?
A) 3,4 m
B) 3,5 m
C) 3,6 m
D) 3,7 m
E) 3,8 m
Questão 5
Sobre os paralelepípedos, julgue as afirmativas a seguir:
I. O paralelepípedo pode ser reto ou oblíquo.
II. As faces de um paralelepípedo são sempre retangulares.
III. Os paralelepípedos são casos particulares de prisma.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Questão 6
Um bloco retangular possui base quadrada e altura de 12 cm. Se o volume desse bloco é igual a 768 cm², o perímetro do quadrado que forma a base desse bloco é:
A) 14 cm
B) 16 cm
C) 20 cm
D) 32 cm
E) 36 cm
Questão 7
Um paralelepípedo reto possui 8 cm de comprimento, 9 cm de largura e 6 cm de altura. Nessas condições, a área total desse paralelepípedo reto é:
A) 696 cm²
B) 522 cm²
C) 348 cm²
D) 232 cm²
E) 174 cm²
Questão 8
A medida da diagonal de um bloco retangular é 5 metros. Se o seu comprimento mede 3,0 metros e sua largura mede 2,4 cm, a altura desse bloco retangular mede aproximadamente:
A) 4,4 m
B) 4,0 m
C) 3,8 m
D) 3,5 m
E) 3,2 m
Questão 9
(Enem 2010) Um porta-lápis de madeira foi construído em formato cúbico, seguindo o modelo ilustrado a seguir. O cubo de dentro é vazio. A aresta do cubo maior mede 12 cm e a do cubo menor, que é interno, mede 8 cm.
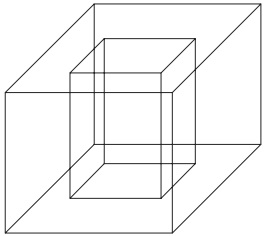
O volume de madeira utilizado na confecção desse objeto foi de:
A) 12 cm³
B) 64 cm³
C) 96 cm³
D) 1216 cm³
E) 1728 cm³
Questão 10
(IFG 2016) Em um certo clube, uma piscina para adultos possui as seguintes dimensões: 30 metros de comprimento, 15 metros de largura e 2 metros de profundidade. Se a piscina está apenas com 2/3 de sua capacidade preenchida, então o número de litros que faltam para preenchê-la totalmente é
A) 200.000 litros.
B) 300.000 litros.
C) 400.000 litros.
D) 500.000 litros.
E) 600.000 litros.
Questão 11
(IFG 2018) Considere um aquário em forma de paralelepípedo reto de base retangular, contendo água até certo nível e com dimensões da base medindo 6 metros e 5 metros. Após a imersão de certo objeto sólido nesse aquário, o nível da água subiu 20 cm sem que água transbordasse.
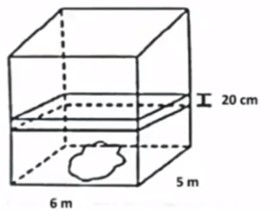
Nessas condições, é correto afirmar que o volume desse objeto sólido, em metros cúbicos, é de
A) 0,6 m³
B) 6 m³
C) 60 m³
D) 600 m³
Questão 12
(Enem 2017) Um casal realiza sua mudança de domicílio e necessita colocar numa caixa de papelão um objeto cúbico, de 80 cm de aresta, que não pode ser desmontado. Eles têm à disposição cinco caixas, com diferentes dimensões, conforme descrito:
• Caixa 1: 86 cm x 86 cm x 86 cm
• Caixa 2: 75 cm x 82 cm x 90 cm
• Caixa 3: 85 cm x 82 cm x 90 cm
• Caixa 4: 82 cm x 95 cm x 82 cm
• Caixa 5: 80 cm x 95 cm x 85 cm
O casal precisa escolher uma caixa na qual o objeto caiba, de modo que sobre o menor espaço livre em seu interior. A caixa escolhida pelo casal deve ser a de número
A) 1
B) 2
C) 3
D) 4
E) 5
Resposta Questão 1
Alternativa D
O paralelepípedo é composto de 12 arestas, 8 vértices e 6 faces.
Resposta Questão 2
Alternativa E
O volume do paralelepípedo reto é o produto das suas dimensões:
\(V=16\cdot12\cdot26\)
\(V=4992\ cm³\)
Resposta Questão 3
Alternativa A
Calculando a área total da caixa do perfume:
\(A_T=2\left(12\cdot3,5+12\cdot8,5+3,5\cdot8,5\right)\)
\(A_T=2\left(42+102+29,75\right)\)
\(A_T=2\cdot173,75\)
\(A_T=347,5\ cm^2\)
A área do embrulho deve ser no mínimo igual a 347,5 cm².
Resposta Questão 4
Alternativa A
Calculando o comprimento da diagonal:
\(d=\sqrt{{1,6}^2+{1,8}^2+{2,4}^2}\)
\(d=\sqrt{2,56+3,24+5,76}\)
\(d=\sqrt{11,56}\)
\(d=3,4\)
A medida da diagonal é 3,4 metros.
Resposta Questão 5
Alternativa B
I. O paralelepípedo pode ser reto ou oblíquo. (verdadeira)
De fato, existem dois grupos de paralelepípedos, os que são retos e os que são oblíquos.
II. As faces de um paralelepípedo são sempre retangulares. (falsa)
As faces de um paralelepípedo não são exclusivamente retangulares, podendo ter formato de qualquer outro paralelogramo.
III. Os paralelepípedos são casos particulares de prisma. (verdadeira)
De fato, os paralelepípedos são casos particulares de prisma.
Resposta Questão 6
Alternativa D
Sabemos que o volume é a área da base vezes a altura. Como a base é um quadrado, sendo x a medida do lado desse quadrado, a área da base será x². Logo:
\(V=A_b\cdot h\)
\(768=x^2\cdot12\)
\(\frac{768}{12}=x^2\)
\(64=x^2\)
\(x=\sqrt{64}\)
\(x=8\ \)
Se o lado do quadrado da base mede 8, o perímetro desse quadrado é igual a:
\(P = 4\cdot8\)
\(P=32\ cm\)
Resposta Questão 7
Alternativa C
Calculando a área total do paralelepípedo:
\(A_T=2\left(8\cdot9+8\cdot6+9\cdot6\right)\)
\(A_T=2\left(72+48+54\right)\)
\(A_T=2\cdot174\)
\(A_T=348\ cm^2\)
Resposta Questão 8
Alternativa E
Sabemos que a diagonal de um bloco retangular é calculada por:
\(d=\sqrt{a^2+b^2+c^2}\)
Sendo c a altura do bloco, substituindo os valores dados:
\(5=\sqrt{3^2+{2,4}^2+c^2}\)
\(5^2=\left(\sqrt{9+5,76+c^2}\right)^2\)
\(25=14,76+c^2\)
\(25-14,76=c^2\)
\(10,26=c^2\)
\(c=\sqrt{10,26}\)
\(c\approx3,2\ \)
Resposta Questão 9
Alternativa D
Como as três arestas possuem a mesma medida, para encontrar o volume do porta-lápis basta elevar:
\(12³ = 1728\)
Mas sabemos que o cubo interno tem lados medindo 8, logo seu volume é de:
\(8³ = 512\)
O volume de madeira é a diferença entre o volume do porta-lápis e o volume do cubo interno:
\(1728-512=1216\ cm^3\)
Resposta Questão 10
Alternativa B
Primeiramente, calcularemos o volume total da piscina:
\(V=15\cdot2\cdot30=900\ m³\)
Sabemos que 2/3 estão cheios, logo falta encher 1/3 dessa piscina. Calculando 1/3 de 900:
\(900\cdot\frac{1}{3}=\frac{900}{3}=300\)
Então, faltam 300 m³. Convertendo m³ em litros:
\(300 \cdot\ 1000 = 300.000 litros\)
Resposta Questão 11
Alternativa B
O volume do objeto é igual ao volume da água contida no paralelepípedo retângulo de lados medindo 6 metros, 5 metros e 20 centímetros.
Para calcular esse volume, antes é importante lembrar que 20 cm = 0,2 m. Logo:
\(V=5\cdot6\cdot0,2\ \)
\(V=5\cdot1,2\ \)
\(V=6\ m^3\)
Resposta Questão 12
Alternativa C
Calculando o volume do objeto, temos que:
\(V={80}^3=512000\)
Sabemos que o objeto tem 80 cm de aresta e que não pode ser desmontado, logo a caixa 2 e a caixa 5 não podem ser utilizadas, já que a primeira possui um lado medindo 75 cm e a segunda, um lado medindo exatamente 80 cm, e a aresta deve ser maior que a medida do objeto.
Agora, calcularemos o volume das demais caixas:
\(V_1=86\cdot86\cdot86=636056\)
\(V_3=85\cdot82\cdot90=627300\)
\(V_4=82\cdot95\cdot82=638780\)
A caixa ideal é a caixa 3, que possui menor volume e dimensões maiores que a do objeto.



