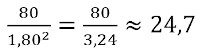Questão 1
Mariana foi até a padaria e comprou um pedaço de torta de frango por R$ 6,50, um copo de suco por R$ 5,25 e, de sobremesa, dois brigadeiros por R$ 0,75 cada. O valor total pago por ela foi de:
A) R$ 13,25
B) R$ 12,50
C) R$ 11,75
D) R$ 10,00
E) R$ 7,50
Questão 2
Para fazer a decoração de Natal, seu Jerivaldo decidiu alugar um forro para a sua mesa. O comprimento e a largura do forro são de 2,20 metros e 1,10 metros, respectivamente. Podemos afirmar que a área da peça é de:
A) 2,30 m²
B) 2,42 m²
C) 2,50 m²
D)2,69 m²
E) 2,85 m²
Questão 3
Durante o ano, um dos itens com valor que sofreu aumentos consecutivos foi a carne bovina. Em um supermercado, no início de janeiro, pagava-se R$ 22,50 pelo quilo de determinada carne. Após os sucessivos aumentos, essa carne passou a custar R$ 39,90 em dezembro. A diferença paga por um cliente que comprou 2,5 kg desse produto em dezembro e em janeiro é igual a:
A) R$ 99,75
B) R$ 56,25
C) R$ 43,50
D) R$ 39,90
E) R$ 30,75
Questão 4
Na figura a seguir, a medida dos lados está dada em metros:
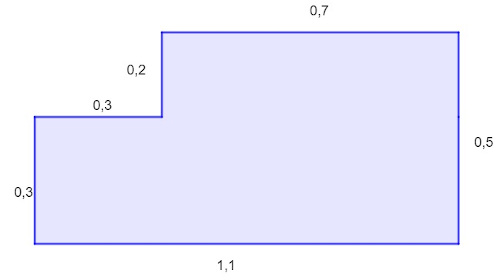
Podemos dizer que o perímetro dessa figura, em metros, é igual a:
A) 1,8
B) 2,1
C) 2,8
D) 3,1
E) 4,0
Questão 5
Ao abastecer seu veículo, um cliente pagou R$ 145,20. Sabendo que o litro de combustível naquele dia custava R$ 6,60, a quantidade de combustível colocada no veículo foi igual a:
A) 11 litros
B) 12 litros
C) 15 litros
D) 18 litros
E) 22 litros
Questão 6
Para ladrilhar determinada região, foram utilizados 32 pisos de cerâmica com 25,8 cm² cada. Portanto, a área dessa região é igual a:
A) 825,6 cm³
B) 735,4 cm³
C) 690,0 cm³
D) 642,2 cm³
E) 512,0 cm³
Questão 7
O Índice de Massa Corporal (IMC) é calculado pela massa dividida pelo quadrado da altura. Uma pessoa que possui 1,80 metro e pesa 80 kg tem um IMC igual a, aproximadamente:
A) 22,8
B) 24,7
C) 25,3
D) 26,0
E) 27,5
Questão 8
Durante a copa do mundo, é comum a venda de figurinhas para álbuns nas bancas de revistas. Durante um mês, uma banca vendeu um total de 823 pacotes de figurinhas. Sabendo que cada pacote é vendido por R$ 2,50, qual foi o faturamento dessa loja com as vendas?
A) R$ 1625,00
B) R$ 1980,00
C) R$ 2057,50
D) R$ 2120,50
E) R$ 2300,00
Questão 9
(Enem 2012) Os hidrômetros são marcadores de consumo de água em residências e estabelecimentos comerciais. Existem vários modelos de mostradores de hidrômetros, sendo que alguns deles possuem uma combinação de um mostrador e dois relógios de ponteiro. O número formado pelos quatro primeiros algarismos do mostrador fornece o consumo em m³, e os dois últimos algarismos representam, respectivamente, as centenas e dezenas de litros de água consumidos. Um dos relógios de ponteiros indica a quantidade em litros e o outro em décimos de litros, conforme ilustrado na figura abaixo:
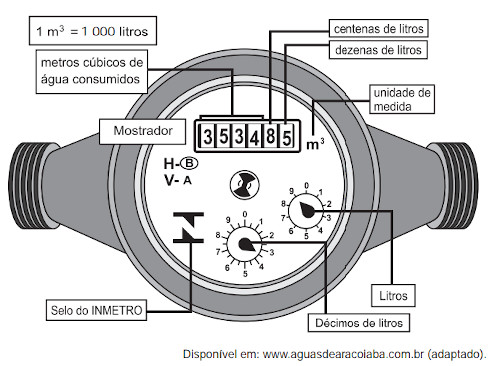
Considerando as informações indicadas na figura, o consumo total de água registrado nesse hidrômetro, em litros, é igual a
A) 3 534,85.
B) 3 544,20.
C) 3 534 850,00.
D) 3 534 859,35.
E) 3 534 850,39.
Questão 10
(Enem 2011 — segunda aplicação) Toda a esfera visível ao longo do ano, nos hemisférios celestes Norte e Sul, está dividida em 88 partes, incluindo, cada uma delas, um número variável de estrelas. A unidade de medida utilizada pelos astrônomos para calcular a área de uma constelação é o grau quadrado. Algumas constelações são imensas, como Erídano, o rio celeste, localizada no hemisfério celeste Sul e ocupa uma área de 1138 graus quadrados. Em contraponto, a constelação Norma, localizada no mesmo hemisfério, não passa de 165 graus quadrados.
Capozzoli, U. Origem e Evolução das Constelações. Scientific American Brasil. Nº 2. 2010.
Em um mapa do hemisfério celestial feito em uma escala de 1:1000, as constelações Erídano e Norma ocuparão, respectivamente, uma área, em graus quadrados, de
A) 0,1138 e 0,0165.
B) 0,1138 e 0,165.
C) 1,138 e 0,165.
D) 11 380 e 1 650.
E) 1 138 000 e 165 000.
Questão 11
(Enem 2011) A tabela compara o consumo mensal, em kWh, dos consumidores residenciais e dos de baixa renda, antes e depois da redução da tarifa de energia no estado de Pernambuco.
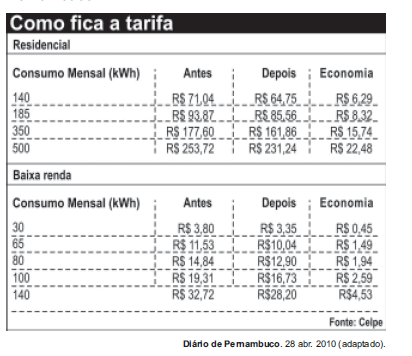
Considere dois consumidores: um que é de baixa renda e gastou 100 kWh e outro do tipo residencial que gastou 185 kWh.
A diferença entre o gasto desses consumidores com 1kWh, depois da redução da tarifa de energia, mais aproximada, é de
A) R$ 0,27.
B) R$ 0,29.
C) R$ 0,32.
D) R$ 0,34.
E) R$ 0,61.
Questão 12
(Enem PPL 2015) Um granjeiro detectou uma infecção bacteriológica em sua criação de 100 coelhos. A massa de cada coelho era de, aproximadamente, 4 kg. Um veterinário prescreveu a aplicação de um antibiótico, vendido em frascos contendo 16 mL, 25 mL, 100 mL, 400 mL ou 1 600 mL. A bula do antibiótico recomenda que, em aves e coelhos, seja administrada uma dose única de 0,25 mL para cada quilograma de massa do animal. Para que todos os coelhos recebessem a dosagem do antibiótico recomendada pela bula, de tal maneira que não sobrasse produto na embalagem, o criador deveria comprar um único frasco com a quantidade, em mililitros, igual a
A) 16.
B) 25.
C) 100.
D) 400.
E) 1 600.
Resposta Questão 1
Alternativa A
Realizando a soma dos números decimais:
6,50 + 5,25 + 2 ∙ 0,75
6,50 + 5,25 + 1,50
13,25
Resposta Questão 2
Resposta Questão 3
Alternativa C
Primeiramente, calcularemos o valor pago por 2,5 kg em janeiro e em dezembro, respectivamente:
2,5 ∙ 22,50 = 56,25
2,5 ∙ 39,90 = 99,75
Agora, calcularemos a diferença entre os valores:
99,75 – 56,25 = 43,50
Resposta Questão 4
Resposta Questão 5
Alternativa E
Para saber a quantidade de combustível necessária, basta realizar a divisão
145,2 : 6,6 = 22
Resposta Questão 6
Alternativa A
Para encontrar o valor da área, basta multiplicar 32 por 25,8:
32 ∙ 25,8 = 825,6 cm³
Resposta Questão 8
Alternativa C
Para calcular o faturamento da loja, basta multiplicar:
823 ∙ 2,50 = 2057,50
Resposta Questão 9
Alternativa D
No mostrador, foi marcado o total de 3534 m³. Para transformar isso em litros, basta multiplicar por 1000. Logo, há um total de 3 534 000 ℓ.
Além disso, há 8 centenas de litros, que equivalem a 800 ℓ, e 5 dezenas de litros, que equivalem a 50 ℓ.
Podemos analisar também que o marcador dos litros está em 9 e o décimo de litros está em 3,5. Assim, temos:
9 ℓ e 0,35 ℓ
Realizando a soma, o consumo do hidrômetro, em litros, é de:
3 534 000 + 800 + 50 + 9 + 0,35 = 3 534 859,35
Resposta Questão 10
Alternativa C
Para aplicar a escala 1:1000, realizaremos a divisão das medidas por 1000:
1138 : 1000 = 1,138
165 : 1000 = 0,165
Resposta Questão 11
Alternativa B
Inicialmente, calcularemos quanto um consumidor residencial paga por 1kWh após a redução da tarifa.
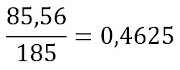
Agora, calcularemos o valor de 1kWh para um consumidor de baixa renda:
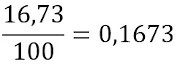
A diferença entre os gastos é dada por:
0,4625 – 0,1673 = 0,2952 ≈ 0,29.
Resposta Questão 12
Alternativa C
Como há 100 coelhos e cada um deles tem massa de aproximadamente 4 kg, deve-se comprar antibiótico para 4 × 100 = 400 kg.
Como para cada quilo é administrado 0,25 mL, faremos a multiplicação de 400 × 0,25 = 100 mg.