Questão 1
O triplo do polinômio 2x³ + 4x² -3x + 1 é:
A) 6x³ + 4x² – 3x + 1
B) 3x9 + 4x6 – 3x³ + 1
C) 6x³ + 12x² – 9x +3
D) 6x9 + 12x6 – 9x³ + 3
Questão 2
As medidas do comprimento, da largura e da altura de uma caixa estão indicadas na imagem a seguir:
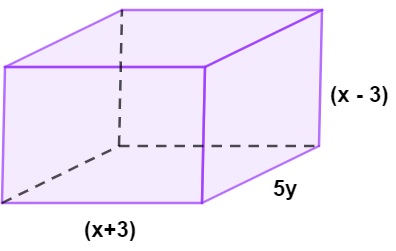
Analisando a imagem, podemos afirmar que o polinômio que descreve o volume da caixa é:
A) 5x²y + 30xy + 45y
B) 5x²y – 30xy + 45y
C) 5x² – 45y
D) 5x²y – 45y
E) 15xy + 3
Questão 3
Seja P(x) o polinômio encontrado quando calculamos o produto entre os polinômios 2x + 4 e – 3x + 2, então a soma dos coeficientes dos termos do polinômio P(x) é igual a:
A) 5
B) 6
C) 7
D) 8
E) 9
Questão 4
Conhecendo os polinômios \(P(x)=3x^3+2x-4\), \(Q(x)=4xy+2x-3\) e \(R(x)=y^4+2xy^2-3\), o grau do polinômio que encontramos quando calculamos o produto \(P(x)⋅Q(x)⋅R(x) \) é:
A) 4
B) 6
C) 7
D) 8
E) 9
Questão 5
As medidas de um terreno estão em função do valor de x e de y, como na imagem a seguir:
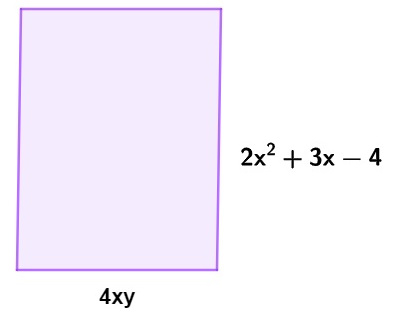
A soma entre os coeficientes do polinômio que descreve a área desse terreno é igual a:
A) 4
B) 5
C) 6
D) 7
E) 8
Questão 6
Considere os polinômios a seguir:
-
X = 3x³ + 3x² + y² + 6
-
Y = -7x² + y²
-
Z = 2x³ – 4x² + y² + 4
O valor da soma 2X + Y – 3Z é igual a:
A) 0
B) 9x²
C) 16y²
D) 3x² + 2y²
E) 4x² – 3x
Questão 7
O raio de um círculo é representado pelo polinômio 3x – 5. Sabendo que a área de um círculo é calculada pela fórmula \(A=πr^2\), o termo independente do polinômio que descreve a área do círculo em questão é:
A) 15
B) 25
C) 15π
D) 25π
E) 30π
Questão 8
Dois terços do polinômio \(3x^3+6x-1\) são iguais ao polinômio:
A) \(9x^3+18x+3\)
B) \(6x^3+12x-2\)
C) \(2x^3+4x-2\)
D) \(2x^3+4x-\frac{2}3\)
Questão 9
A seguir, temos a imagem de um trapézio:
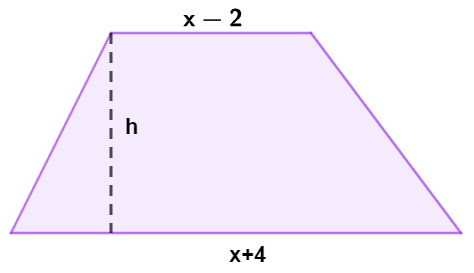
A área desse trapézio pode ser descrita pelo polinômio:
A) \(xh-h \)
B) \(6xh-h \)
C) \(3xh-3h \)
D) \(4xh-4h \)
E) \(2xh-2h \)
Questão 10
Sobre a multiplicação de polinômios, julgue as afirmativas a seguir:
I. Para multiplicar um número natural por um polinômio, multiplicamos os coeficientes dos termos do polinômio por esse número natural.
II. A multiplicação entre dois polinômios do primeiro grau gera um polinômio também do primeiro grau.
III. O zero é o elemento neutro da multiplicação de polinômios.
Marque a alternativa correta:
A) Somente a I é verdadeira.
B) Somente a II é verdadeira.
C) Somente a III é verdadeira.
D) Todas são falsas.
Questão 11
Ao realizar a multiplicação entre um polinômio de grau 8 e um polinômio de grau 2, o grau do polinômio encontrado será:
A) 2
B) 8
C) 10
D) 12
E) 16
Questão 12
O produto entre os polinômios (x – 4) e (x + 4) é o polinômio:
A) x² + 8x + 16
B) x² + 2x + 4
C) x² – 8x + 16
D) x² – 16
E) x² + 16
Resposta Questão 1
Alternativa C
Para calcular a multiplicação entre um polinômio e um número real, temos que:
\(3⋅(2x^3+4x^2-3x+1)\)
\(3⋅2x^3+3⋅3x^2-3⋅3x+3⋅1\)
\(6x^3+12x^2-9x+3\)
Resposta Questão 2
Alternativa D
Para calcular o volume da caixa, basta multiplicar as três dimensões:
\(V=(x+3)⋅(x-3)⋅5y\)
\(V=(x^2+3x-3x-9)⋅5y\)
\(V=(x^2-9)⋅5y\)
\(V=5x^2 y-45y\)
Resposta Questão 3
Alternativa B
Calculando o produto entre os polinômios, temos que:
\((2x+4)(3x-2)\)
\(6x^2-4x+12x-8\)
\(6x^2+8x-8\)
Somando os coeficientes, temos que:
6 + 8 – 8 = 6
Resposta Questão 4
Alternativa E
Para calcular o grau do produto desses polinômios, multiplicaremos os termos de maior grau de cada um deles, logo, temos que:
\(3x^3⋅4xy⋅y^4=12x^4 y^5\)
Somando os expoentes da parte literal 4 + 5 = 9, então o grau do polinômio encontrado quando calculamos o produto entre P(x), Q(x) e R(x) é 9.
Resposta Questão 5
Alternativa A
Para calcular a área do terreno, multiplicaremos o monômio 4xy pelo polinômio 2x² +3x – 4, logo, temos que:
\(4xy⋅(2x^2+3x-4)\)
\(8x^3 y+12x^2 y-16xy\)
Calculando a soma dos coeficientes, temos que:
\(8+12-16=20-16=4\)
Resposta Questão 6
Alternativa B
Primeiro calcularemos 2X:
\(2X=2(3x^3+2x^2+y^2+6)\)
\(2X=6x^3+4x^2+2y^2+12\)
Agora calcularemos -3Z:
\(-3Z=-3(2x^3-4x+y^2+4)\)
\(-3Z=-6x^3+12x²-3y^2-12\)
Somando 2X + Y – 3Z:
\((6x^3+4x^2+2y^2+12)+(-7x^2+y^2 )+(-6x^3+12x²-3y^2-12)\)
Somando os termos semelhantes:
\(0x^3+9x^2+0y^2+0\)
\(9x^2\)
Resposta Questão 7
Alternativa D
Calculando a área do círculo, temos que:
\(A=πr^2\)
\(A=π(3x-5)^2\)
\(A=π(3x-5)(3x-5)\)
\(A=π(9x^2-15x-15x+25)\)
\(A=9πx^2-30πx+25π\)
Então o termo independente é 25π.
Resposta Questão 8
Alternativa D
Calculando a multiplicação do polinômio por \(\frac{2}3\), temos que:
\(\frac{2}3 (3x^3+6x-1)\)
\(\frac{6}3 x^3+\frac{12}3 x-\frac{2}3\)
\(2x^3+4x-\frac{2}3\)
Resposta Questão 9
Alternativa A
Calculando a área, temos que:
\(A=\frac{(B+b)h}2\)
\(A=\frac{(x+4+x-2)h}2\)
\(A=\frac{(2x-2)h}2\)
\(A=\frac{2xh-2h}2\)
\(A=xh+h \)
Resposta Questão 10
Alternativa A
I. Para multiplicar um número natural por um polinômio, multiplicamos os coeficientes dos termos do polinômio por esse número natural. (Verdadeiro)
II. A multiplicação entre dois polinômios do primeiro grau gera um polinômio também do primeiro grau. (Falso)
Na multiplicação de polinômios de primeiro grau, o resultado será um polinômio do segundo grau.
III. O zero é o elemento neutro da multiplicação de polinômios. (Falso)
O 1 é o elemento neutro da multiplicação de polinômios.
Resposta Questão 11
Alternativa C
Para encontrar o grau do polinômio que é resultado da multiplicação entre um polinômio de grau 8 e um polinômio de grau 2, basta calcularmos a soma dos graus, ou seja 8 + 2 = 10.
Resposta Questão 12
Alternativa D
Calculando a multiplicação, temos que:
\((x-4)⋅(x+4)=x^2+4x-4x - 16\)
\((x-4)⋅(x+4)=x^2-16\)



