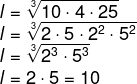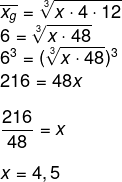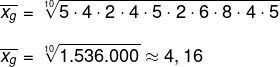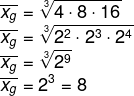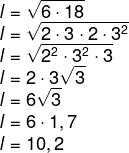Questão 1
A média geométrica entre os números 12, 27, 4 e 1 é igual a:
A) 36
B) 24
C) 12
D) 6
E) 3
Questão 2
Um cubo possui volume equivalente ao de um prisma com comprimento igual a 10 cm, largura igual a 4 cm e altura igual a 25 cm, então, a medida do lado do cubo em centímetros é de:
A) 5 cm
B) 8 cm
C) 10 cm
D) 12 cm
E) 15 cm
Questão 3
O valor de uma ação na bolsa de valores sofreu grande oscilação durante a semana. No primeiro dia, ela teve um aumento de 5%; no segundo dia, de 16%. No terceiro e quarto dias, ela se manteve constante. No quinto e no sexto dias, houve um aumento de 27% e 25%, respectivamente, e no sétimo dia, ela se manteve com o valor do dia anterior. Calculando a média geométrica entre as quatro oscilações ocorridas, encontraremos:
A) Aumento de aproximadamente 18%.
B) Aumento de aproximadamente 16%.
C) Aumento de aproximadamente 15%.
D) Aumento de aproximadamente 13%.
E) Aumento de aproximadamente 11%.
Questão 4
A média entre os números x, 4 e 12 é igual a 6, então, o valor de x é:
A) 3
B) 3,5
C) 4
D) 4,5
E) 5
Questão 5
A diferença entre a média aritmética e a média geométrica do conjunto A {4,6,8,10} é, aproximadamente, igual a:
A) 0,38
B) 0,44
C) 0,45
D) 0,52
E) 0,63
Questão 6
(IBFC) A média geométrica aproximada dos dois casos abaixo está descrita na alternativa:
|
|
10/set |
15/set |
20/set |
25/set |
30/set |
|
Caso 1 |
5 |
4 |
2 |
4 |
5 |
|
Caso 2 |
2 |
6 |
8 |
4 |
5 |
A) 2,41
B) 4,16
C) 5,16
D) 5,54
E) 2,92
Questão 7
Determinado investimento teve um aumento de 4% no primeiro mês; no segundo mês, um aumento de 5%; e no terceiro mês, um aumento de 10%, então, o rendimento médio do investimento feito é, aproximadamente, de:
A) 4%
B) 5%
C) 6%
D) 7%
E) 8%
Questão 8
(FCC) A média geométrica dos números 4, 8 e 16 é:
A) maior que a respectiva média aritmética.
B) inferior a 6.
C) igual a 8.
D) igual a 4.
E) superior a 9.
Questão 9
Analise os conjuntos a seguir:
A = {2, 6, 30} e B = {3, 5, 24}
Calculando a média geométrica e a média aritmética de cada um dos conjuntos, podemos afirmar que:
A) A média geométrica de A é maior que a média geométrica de B.
B) A média geométrica de B é maior que a média geométrica de A.
C) A média geométrica de A é igual à média geométrica de B.
D) A média geométrica de B é igual a 360.
E) A média geométrica de A é igual a 60.
Questão 10
(CKM) Ana, Bruna e Camila estudam em escolas diferentes com professoras de matemática diferentes, e estas usam métodos diferentes para determinar a média de nota de prova obtida por seus alunos. A professora de Ana utiliza o método da média ponderada, enquanto que as professoras de Bruna e Camila utilizam, respectivamente, a média aritmética e a média geométrica. Sabendo que tanto a professora de Ana como as professoras de Bruna e Camila aplicam três provas durante o bimestre, considere a tabela a seguir, que contém as notas obtidas por Ana, Bruna e Camila nas provas que cada uma delas realizou no primeiro bimestre de 2013.
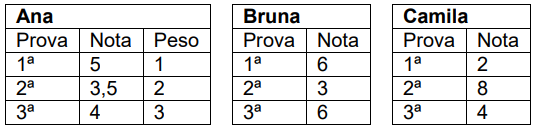
Assinale, a seguir, a alternativa que apresenta, respectivamente, a média de nota de prova obtida por Ana, Bruna e Camila de acordo com o método utilizado por suas respectivas professoras:
A) 4, 5 e 4
B) 5, 4 e 4
C) 4, 4 e 5
D) 4, 5 e 5
E) 5, 5 e 4
Questão 11
Em uma fábrica que produz embalagens, entre as fabricações há uma caixa com base retangular cujas bases medem 6 cm e 18 cm. Para atender a um pedido de um cliente, foram fabricadas caixas com bases quadradas que ocupassem a mesma área que a caixa de base retangular. Então, a medida do lado da nova caixa é: (Dado: √3 = 1,7)
A) 10,0 cm
B) 10,2 cm
C) 12,0 cm
D) 20,1 cm
E) 13,7 cm
Questão 12
(Mackenzie - adaptada) Se a média aritmética entre dois números é 30 e a geométrica é 18, então o módulo da diferença entre esses dois números é:
A) 45
B) 60
C) 50
D) 48
E) 52
Resposta Questão 1
Alternativa D
Calculando a média geométrica, temos que:
\(\overline{x_g}=\sqrt[4]{12⋅27⋅4⋅1}\)
\(\overline{x_g}=\sqrt[4]{2^2⋅3⋅3^3⋅2^2⋅1}\)
\(\overline{x_g}=\sqrt[4]{2^4⋅3^4⋅1}\)
\(\overline{x_g}=2⋅3⋅1=6\)
Resposta Questão 2
Resposta Questão 3
Alternativa A
Transformando em números decimais, temos que:
Aumento de 5% → 1,05
Aumento de 16% → 1,16
Aumento de 27% → 1,27
Aumento de 25% → 1,25
Então, calculando a média geométrica entre esses números, temos que:
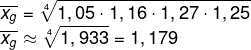
Resposta Questão 5
Alternativa A
Calculando a média geométrica, temos que:
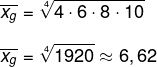
Agora, calculando a média aritmética, temos que:
![]()
A diferença entre a média aritmética e a geométrica é 7 – 6,62 = 0,38.
Resposta Questão 7
Alternativa C
Aumento de 4% → 1,04
Aumento de 5% → 1,05
Aumento de 10% → 1,1
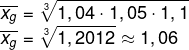
O aumento foi de, aproximadamente, 6%.
Resposta Questão 9
Alternativa C
Calculando a média geométrica do conjunto A e do conjunto B, temos que:
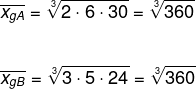
As médias geométricas são iguais.
Resposta Questão 10
Alternativa A
Calculando a nota de Ana pela média ponderada, temos que:
![]()
Calculando a nota de Bruna por média aritmética, temos que:
![]()
Calculando a nota da Camila por média geométrica, temos que:
![]()
Então as médias são 4, 5 e 4.
Resposta Questão 11
Resposta Questão 12
Alternativa D
Seja x e y os números, pela média aritmética, temos que:
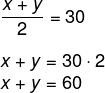
Pela média geométrica, temos que:
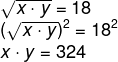
Então, para encontrar o valor de x e y, vamos utilizar o sistema de equações. Isolando a primeira equação e substituindo na segunda, temos que:
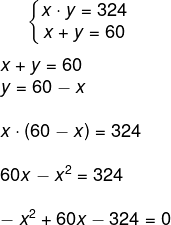
Resolvendo a equação do segundo grau, temos que:
a = -1
b = 60
c = -324
Δ = b² – 4ac
Δ = 60² – 4 (-1) (-324)
Δ = 3600 – 1296
Δ = 2304
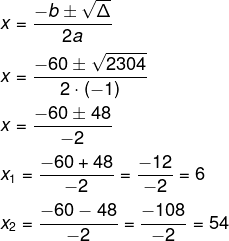
Existem dois resultados possíveis. Se x = 6, sabemos que:
x + y = 60
6 + y = 60
y = 60 – 6
y = 54
Se x = 54
54 + y = 60
y = 60 – 54
y = 6
Então, a diferença entre x e y em módulo é |54 – 6| ou |6 – 54|. Como, em ambos os casos, o resultado é o mesmo, temos que:
|54 – 6| = |6 – 54| = |48| = 48