Questão 1
Sobre as matrizes, julgue as afirmativas a seguir:
I – A matriz linha é aquela que possui uma única linha.
II – A matriz coluna é aquela que possui uma única coluna.
III – A matriz quadrada é aquela que possui número de linhas igual ao número de colunas.
Marque a alternativa correta:
A) Somente I é falsa.
B) Somente II é falsa.
C) Somente III é falsa.
D) Todas são verdadeiras.
Questão 2
Analise a matriz a seguir:
\(\left(\begin{matrix}1&5&1\\3&4&0\\1&-2&-3\\\end{matrix}\right)\)
A soma dos termos \(a_{22}\ e{\ a}_{32}\) é igual a:
A) -1
B) -2
C) 0
D) 1
E) 2
Questão 3
(Uerj — adaptada) A temperatura corporal de um paciente foi medida, em graus Celsius, três vezes ao dia (de manhã, de tarde e de noite), durante cinco dias. Cada elemento aij da matriz abaixo corresponde à temperatura observada no instante i do dia j.

Julgue as afirmativas a seguir:
I - No momento a21, o paciente estava com a temperatura de 36,1.
II - As temperaturas do momento a33 e do momento a21 são iguais.
III - No momento \(a_{35}\), a temperatura era de 39,2.
A ordem correta é:
A) V V V
B) V F V
C) F V V
D) F F V
E) V V F
Questão 4
(Enem 2012) Um aluno registrou as notas bimestrais de algumas de suas disciplinas numa tabela. Ele observou que as entradas numéricas da tabela formavam uma matriz 4x4 e que poderia calcular as médias anuais dessas disciplinas usando produto de matrizes. Todas as provas possuíam o mesmo peso, e a tabela que ele conseguiu é mostrada a seguir:
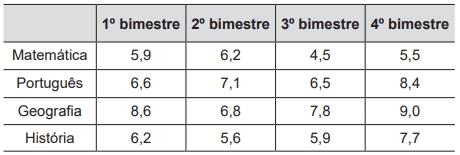
Para obter essas médias, ele multiplicou a matriz obtida na tabela por
A) \(\left[\begin{matrix}\frac{1}{2}&\frac{1}{2}&\frac{1}{2}&\frac{1}{2}\\\end{matrix}\right]\)
B) \(\left[\begin{matrix}\frac{1}{4}&\frac{1}{4}&\frac{1}{4}&\frac{1}{4}\\\end{matrix}\right]\)
C) \(\left[\begin{matrix}1\\1\\1\\1\\\end{matrix}\right]\)
D) \(\ \left[\begin{matrix}\frac{1}{2}\\\frac{1}{2}\\\frac{1}{2}\\\frac{1}{2}\\\end{matrix}\right]\)
E) \(\ \left[\begin{matrix}\frac{1}{4}\\\frac{1}{4}\\\frac{1}{4}\\\frac{1}{4}\\\end{matrix}\right]\)
Questão 5
Uma matriz \(A_{5x5}\) possui lei de formação \(a_{ij}=5i-j^2\). A soma dos termos da diagonal principal é igual a:
A) 12
B) 15
C) 18
D) 20
E) 25
Questão 6
Uma matriz quadrada de ordem 2 possui lei de formação \(b_{ij}=2i+3i-5\). Portanto, a matriz B é:
A) B = \( \left[\begin{matrix}0&5\\3&1\\\end{matrix}\right]\)
B) B = \( \left[\begin{matrix}0&3\\2&5\\\end{matrix}\right]\)
C) B = \(\left[\begin{matrix}4&0\\2&-3\ \\\end{matrix}\right]\)
D) B = \(\left[\begin{matrix}1&3\\0&2\\\end{matrix}\right]\)
E) B = \(\left[\begin{matrix}5&3\\2&0\\\end{matrix}\right]\)
Questão 7
Considere a matriz \(A=\left[\begin{matrix}4&5\\2&3\\\end{matrix}\right]\) e a matriz B = \(\left[\begin{matrix}4&2y\ +\ 1\\3x\ -\ 4&3\\\end{matrix}\right]\). Sabendo que as matrizes A e B são iguais, o valor de x + y é igual a:
A) 3
B) 4
C) 5
D) 6
E) 7
Questão 8
Considere a matriz \(=\left[\begin{matrix}x\ -\ 4&15\\2&3\\\end{matrix}\right]\). Sabendo que o seu determinante é igual a 15, o valor de x é:
A) 15
B) 16
C) 18
D)19
E) 20
Questão 9
(Prefeitura de Bombinhas – SC) É correto afirmar que:
A) A matriz unitária é uma matriz quadrada que possui todos os elementos da diagonal principal iguais a 1 e os demais elementos iguais a 0.
B) Duas matrizes, A = [aij]mxn e B = [bij]nxm, são opostas se, e somente se, aij = bji.
C) Uma matriz é quadrada quando o número de linhas é igual ao número de colunas.
D) Uma matriz é dita nula se todos os seus elementos são diferentes de zero.
Questão 10
Analise a matriz A a seguir:
\(A\ =\ \left(\begin{matrix}1&3&4\\-2&5&9\\-1&2&7\\\end{matrix}\right)\)
A diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária é:
A) 15
B) 20
C) 35
D) 55
E) 80
Questão 11
Qual deve ser o valor de x para que
\(\left|\begin{matrix}2&log3\\2&logx\\\end{matrix}\right|=0\)
A) – 3 ou 3
B) – 2 ou 2
C) 0
D) 2
E) 3
Questão 12
(UFRGS) A matriz C fornece, em reais, o custo das porções de arroz, carne e salada usados em um restaurante. A matriz P fornece o número de porções de arroz, carne e salada usados na composição dos pratos tipo P1, P2 e P3.
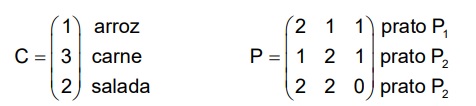
A matriz que fornece o custo de produção, em reais, dos pratos P1, P2 e P3 é:
A) \( \left(\begin{matrix}7\\9\\8\\\end{matrix}\right)\)
B) \( \left(\begin{matrix}4\\4\\4\\\end{matrix}\right)\)
C) \( \left(\begin{matrix}9\\11\\4\\\end{matrix}\right)\)
D) \( \left(\begin{matrix}2\\8\\6\\\end{matrix}\right)\)
Resposta Questão 1
Alternativa D
I – Verdadeira
A matriz linha é aquela que tem 1 única linha.
II – Verdadeira
A matriz coluna é aquela que possui 1 única coluna.
III – Verdadeira
De fato, a matriz quadrada é aquela que tem o mesmo número de linhas e colunas.
Resposta Questão 2
Alternativa E
O termo \(a_{32}\) é aquele que está na terceira linha e segunda coluna, ou seja:
\(a_{32}=-2\)
O termo \(a_{22}\) é aquele que está na primeira linha e segunda coluna, ou seja:
\(a_{22}=4\)
A soma entre esses termos é:
\(-\ 2+4=2\)
Resposta Questão 3
Alternativa A
I - Verdadeira
O termo que ocupa a 2ª linha e 1ª coluna de fato é 36,1.
II - Verdadeira
As duas temperaturas são iguais a 36,1.
III - Verdadeira
O termo que está na 3ª linha e 5ª coluna é 39,2.
Resposta Questão 4
Alternativa E
A multiplicação da matriz é feita entre a linha e a coluna. Logo, é necessário que ela seja uma matriz 4x1.
Além disso como há 4 notas, a média será a soma de \(\frac{1}{4} \) de cada uma das médias. Assim, a alternativa que contém a matriz que devemos multiplicar pela matriz das notas é a alternativa E.
Resposta Questão 5
Alternativa D
Os termos da diagonal principal são:
\(a_{11}=5\cdot1-1^2=5-1=4\)
\(a_{22}=5\cdot2-2^2=10-4=6\)
\(a_{33}=5\cdot3-3^2=15-9=6\)
\(a_{44}=5\cdot4-4^2=20-16=4\)
\(a_{55}=5\cdot5-5^2=25-25=0\)
Então, a soma dos termos da diagonal é:
4 + 6 + 6 + 4 + 0 = 20
Resposta Questão 6
Alternativa B
A matriz de ordem 2 possui 2 linhas e 2 colunas. Assim, de forma algébrica, a matriz B é:
\(B=\left[\begin{matrix}b_{11}&b_{12}\\b_{21}&b_{22}\\\end{matrix}\right]\)
Calculando cada termo:
\(b_{11}=2\cdot1+3\cdot1-5=2+3-5=0\)
\(b_{12}=2\cdot1+3\cdot2-5=2+6-5=3\)
\(b_{21}=2\cdot2+3\cdot1-5=4+3-5=2\)
\(b_{22}=2\cdot2+3\cdot2-5=4+6-5=5\)
Então, a matriz B é:
\(B=\left[\begin{matrix}0&3\\2&5\\\end{matrix}\right]\)
Resposta Questão 7
Alternativa B
Para que as matrizes sejam iguais, temos:
\(2y+1\ =5\ \)
\(2y=5\ –1 \)
\(2y=4\ \)
\(y=\frac{4}{2}\)
\(y=2\)
Calculando o valor de x:
\(3x-4=2\)
\(3x=2+4\)
\(3x=6\)
\(x=\frac{6}{3}\)
\(x=2\)
Então:
x + y = 2 + 2 = 4
Resposta Questão 8
Alternativa D
Calculando o determinante:
\(det\left(A\right)=3\cdot\left(x-4\right)-15\cdot2\)
\(det\left(A\right)=3x-12-30\)
\(det\left(A\right)=3x-42\)
Como detA=15:
\(3x-42=15\)
\(3x=15+42\)
\(3x=57\)
\(x=\frac{57}{3}\)
\(x=19\)
Resposta Questão 9
Alternativa C
A matriz é quadrada quando possui o mesmo número de linhas e colunas.
Resposta Questão 10
Alternativa D
Calculando o produto da diagonal principal menos o produto da diagonal secundária:
\(1\cdot5\cdot7-4\cdot\left(-1\right)\cdot5=35+\ 20=55\)
Resposta Questão 11
Alternativa E
Calculando o determinante:
\(2logx-2log3=0\)
\(2logx=2log3\)
Dividindo por 2 em ambos os lados:
\(logx=log3\ \)
\(x=3\)
Resposta Questão 12
Alternativa A
Calcularemos o produto entre as matrizes:
\(\left(\begin{matrix}2&1&1\\1&2&1\\2&2&0\\\end{matrix}\right)\cdot\left(\begin{matrix}1\\3\\2\\\end{matrix}\right)=\left(\begin{matrix}2\cdot1+1\cdot3+1\cdot2\\1\cdot1+2\cdot3+1\cdot2\\2\cdot1+3\cdot2+0\cdot2\\\end{matrix}\right)\ =\left(\begin{matrix}2+3+2\\1+6+2\\2+6+0\\\end{matrix}\right)=\left(\begin{matrix}7\\9\\8\\\end{matrix}\right)\)



