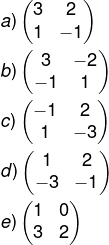Questão 2
Sabendo que as matrizes A e B são inversas, x e y são, respectivamente:
![]()
A) x = 4 e y = 2
B) x = -3 e y = -1
C) x = 5/2 e y = -2/3
D) x = -1/2 e y = 5/4
E) x = -1 e y = 1/2
Questão 3
Dada uma matriz A, sabemos que ela pode ter uma matriz inversa ou não. Para isso, calculamos o determinante da matriz. Sobre a matriz A, a seguir, podemos afirmar que:
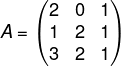
A) A matriz admite inversa, já que o seu determinante é igual a 0.
B) A matriz admite inversa, já que o seu determinante é diferente de 0.
C) A matriz não admite inversa, já que o seu determinante é igual a 0.
D) A matriz não admite inversa, já que o seu determinante é diferente de 0.
Questão 4
Dada a matriz M e a matriz M-1, podemos afirmar que o valor de x + y é:
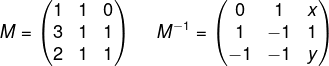
A) -2
B) -1
C) 0
D) 1
E) 2
Questão 5
A matriz B é uma matriz quadrada e não inversível. Sendo assim, o valor de x é:
![]()
A) 0
B) 1
C) 2
D) -2
E) -1
Questão 6
Sobre a matriz inversa, julgue as afirmativas a seguir:
I – A matriz é inversível se o seu determinante for diferente de zero.
II – A matriz inversa da matriz identidade é ela mesma.
III – Uma matriz 3x2 pode admitir inversa.
Marque a alternativa que contém o julgamento correto respectivamente:
A) F, F, F
B) V, V, V
C) F, V, V
D) V, V, F
E) V, F, F
Questão 7
(Unicamp) Considere a matriz quadrada A de ordem 3, onde x é um número real:
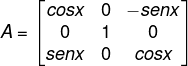
Podemos afirmar que:
A) A não é inversível para nenhum valor de x.
B) A é inversível para um único valor de x.
C) A é inversível para exatamente todos os valores de x.
D) A é inversível para todos os valores de x.
Questão 8
(Cefet MG) A matriz A é inversa de B. Pode-se afirmar que a diferença x – y é igual a:
![]()
A) -8
B) -2
C) 2
D) 6
E) 8
Questão 9
(UFU MG - adaptada) Considere o conjunto das matrizes da forma:
![]()
O valor de k para que a matriz exista exatamente como uma matriz inversível nesse conjunto é:
A) -21/4
B) 12/5
C) -7/2
D) 3/5
E) 4/9
Questão 10
Seja B a matriz inversa de A, sabendo que a matriz A é de ordem dois em que os termos são aij = i + j, o termo que ocupa a posição b22 da matriz B é:
A) 0
B) 1
C) 2
D) -1
E) -2
Questão 11
Sobre a matriz inversa, julgue as afirmativas a seguir:
I – Toda matriz quadrada admite matriz inversa.
II – A matriz nula não admite matriz inversa.
III – A inversa da matriz A-1 é a matriz A.
Agora marque a alternativa que corresponde ao julgamento correto:
A) F, F, V
B) V, V, F
C) F, V, V
D) V, F, F
E) V, F, V
Questão 12
Quais são os valores de x que fazem com que a matriz não seja inversível?
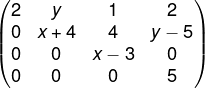
A) x = 0 ou x = 5
B) x = 4 ou x = 5
C) x = 2 ou x = 1
D) x = -3 ou x = 4
E) x = 3 ou x = -4
Resposta Questão 1
Alternativa B
Dada a matriz A, para encontrar a inversa da matriz, vamos resolver a equação:
A · A-1 = I
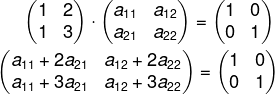
Montando o primeiro sistema e analisando a primeira coluna, temos que:
![]()
Isolando a11 na equação II, temos que:
a11 = -3a21
Substituindo em I:
a11 + 2a21 = 1
– 3a21 + 2a21 = 1
– a21 = 1 (-1)
a21 = -1
Tendo o valor de a21, é possível encontrar o valor de a11:
a11 = -3a21
a11 = -3 (-1)
a11 = 3
Agora vamos analisar a segunda coluna para montar o segundo sistema:
![]()
Isolando a12 em III, temos:
a12 = -2a22
Substituindo em IV:
a12 + 3a22 =1
– 2a22 + 3a22 = 1
a22 = 1
Conhecendo o valor de a22, encontraremos o valor de a12:
a12 = -2 a22
a12 = -2 · 1
a12 = -2
Representando a matriz inversa, temos:
![]()
Resposta Questão 2
Alternativa D
Como B é a inversa de A, então, montando a equação, temos que:
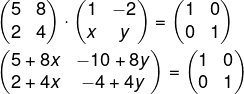
Agora podemos escolher uma equação com x, para encontrar o valor de x, e uma equação com y, para encontrar o valor de y.
Escolhendo o termo que está na segunda linha, primeira coluna, temos que:
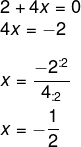
Para encontrar o valor de y, utilizaremos o termo da segunda coluna, primeira linha:
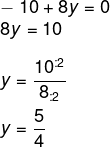
Resposta Questão 3
Alternativa B
Para verificar se a matriz admite inversa, basta calcular o determinante da matriz, caso ele seja 0, a matriz não é inversível:
Det(A) = 2 · 2 · 1 + 0 · 1 · 3 + 1 · 1 · 2 – (1 · 2 · 3 + 2 · 1 · 2 + 0 · 1 ·1)
Det(A) = 4 + 0 + 2 – (6 + 4)
Det(A) = 6 – 10
Det(A) = -4
Como o determinante da matriz é diferente de 0, a matriz é inversível.
Resposta Questão 4
Alternativa D
Montando a equação matricial, sabendo que M · M-1 = In:
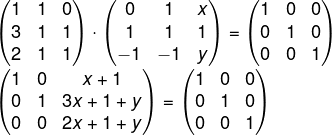
Pela terceira coluna, temos que:
x + 1 = 0
x = -1
Conhecendo o valor de x, basta escolher qualquer uma das outras equações da terceira coluna para encontrar o valor de y.
3x + 1 + y = 0
3 (-1) + 1 + y = 0
– 3 + 1 + y = 0
– 2 + y =0
y = 2
Então:
x + y = – 1 + 2 = 1
Resposta Questão 5
Alternativa C
Para que a matriz não seja inversível, seu determinante tem que de ser igual a zero:
det(B) = 3x – 6 · 1
det(B) = 3x – 6
3x – 6 = 0
3x = 6
x = 6/3
x = 2
Resposta Questão 6
Alternativa D
I → Verdadeira, pois, se det(A) for diferente de zero, a matriz admite inversa.
II → Verdadeira, pois In · In = In.
III → Falsa, para que uma matriz admita inversa, ela precisa ser uma matriz quadrada, ou seja, ter o mesmo número de linhas e colunas.
Resposta Questão 7
Alternativa B
Calculando o determinante da matriz, temos que:
det(A) = cosx · 1 · cosx + 0 · 0 · senx + (-senx) · 0 · 0 – [ – senx · 1 · senx + cosx · 0 · 0 + 0 · 0 · cosx]
det(A) = cos²x + 0 + 0 – [– sen²x + 0 + 0]
det(A) = cos²x – [-sen²x]
det(A) = cos²x + sen²x
Pelo teorema fundamental da trigonometria, cos²x + sen²x = 1 para todo valor de x, ou seja:
det(A) = 1
Como ele é diferente de 0, então a matriz é inversível para qualquer valor de x.
Resposta Questão 8
Alternativa E
Montando a equação e igualando os termos da matriz, temos que:
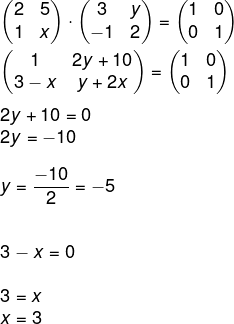
Então:
x – y = 3 – (-5) = 3 + 5 = 8
Resposta Questão 9
Alternativa A
Calculando o determinante da matriz, temos que:
det(M) = (x – 3) (x – 5) – (x + k)
det(M) = x² – 5x – 3x + 15 – x – k
det(M) = x² – 9x + 15 – k
Como a matriz não é inversível, então det(M) = 0.
x² – 9x + 15 – k = 0
Encontramos uma equação do 2º grau. Como queremos que exista exatamente uma matriz inversível no conjunto, Δ = 0, pois, quando Δ = 0, existe um único valor que faz com que a equação seja igual a 0.
a = 1
b = -9
c = 15 – k
Δ = b² – 4ac
Δ = (-9)² – 4 · 1 · (15 – k)
Δ = 81 – 60 + 4k
Δ = 21 + 4k
21 + 4k = 0
4k = -21
k = -21/4
Resposta Questão 10
Alternativa E
Primeiro construiremos a matriz A:
a11 = 1 + 1 = 2
a12 = 1 + 2 = 3
a21 = 2 + 1 = 3
a22 = 2 + 2 = 4
Então a matriz A será:
![]()
Encontrando a inversa de A, temos que:
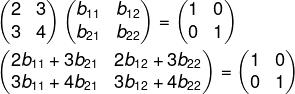
Como o nosso interesse é só no termo b22, vamos analisar as duas equações da segunda coluna, então montaremos o sistema e o resolveremos pelo método da substituição:
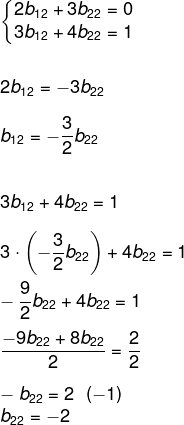
Resposta Questão 11
Alternativa C
I → Falsa, pois se o determinante for zero, a matriz quadrada não admite inversa.
II → Verdadeira, pois o determinante da matriz nula é 0, logo, ela não admite inversa.
III → Verdadeira, pois A-1 · A = In.
Resposta Questão 12
Alternativa E
Como a matriz é triangular superior, seu determinante é o produto dos elementos da diagonal principal. Para que ela não seja inversível, seu determinante deve ser igual a zero.
det(A) = 2 · (x + 4) · (x – 3) · 5
Para que essa multiplicação seja igual a 0, uma das parcelas deve ser zero, ou seja:
x + 4 = 0 → x = -4 ou
x – 3 = 0 → x = 3