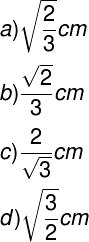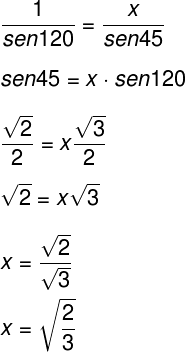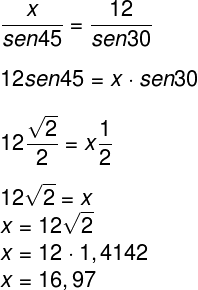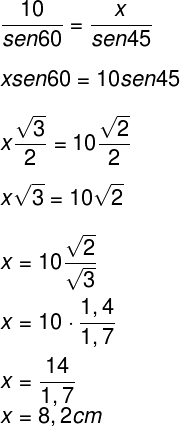Questão 1
(UFU-MG) Considere o triângulo retângulo a seguir.
Sabendo-se que α = 120°, AB = AC = 1 cm, então AD é igual a:
Questão 2
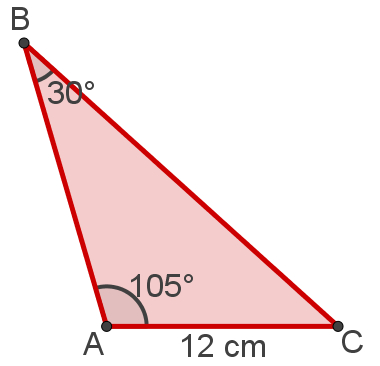
(Mackenzie – SP) Três ilhas A, B e C aparecem num mapa em escala 1:10000, como na figura. Das alternativas, a que melhor se aproxima de distância entre as ilhas A e B é:
a) 2,3 km
b) 2,1 km
c) 1,9 km
d) 1,4 km
e) 1,7 km
Questão 3
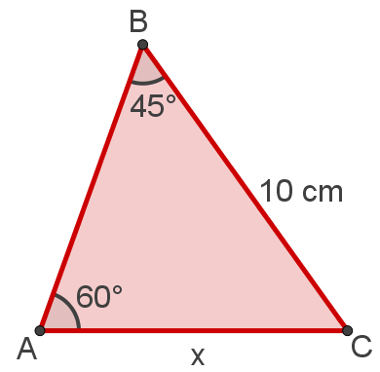
No triângulo a seguir, determine a medida do lado AC, tendo em vista as medidas presentes nele. (Use √2 = 1,4 e √3 = 1,7).
a) 8,2 cm
b) 12,2 cm
c) 14 cm
d) 17 cm
e) 17,2 cm
Questão 4
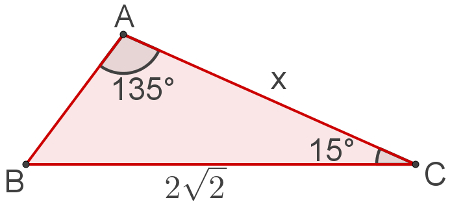
No triângulo a seguir, qual é a medida do segmento AC, destacada pela letra x, dado que essas medidas estão em centímetros?
a) 2 cm
b) 2√3 cm
c) 3√2 cm
d) 3√3 cm
e) 4√2 cm
Resposta Questão 1
Para resolver esse exercício, observe que o triângulo é isósceles, pois AB = AC = 1 cm. Portanto, os ângulos B e C são iguais a 45°, uma vez que eles são iguais porque são os ângulos da base do triângulo isósceles. Considerando apenas o triângulo ABD, já temos a medida de dois lados e dos ângulos opostos a ele (uma dessas medidas é a que queremos descobrir: AD). Sabendo que sen120° = sen45°, podemos usar a lei dos senos:
Alternativa: A
Resposta Questão 2
Observe que o segmento AB é oposto ao ângulo C. Pela soma das medidas internas de um triângulo, concluímos que o ângulo C mede 45°. Os lados que serão usados nesse problema são AC = 12 cm e AB = x. Os ângulos opostos a esses lados são: 30° e 45°, respectivamente. Na lei dos senos, temos:
O resultado obtido está em centímetros, portanto, convertendo para metros por meio da escala e depois convertendo metros para quilômetros, teremos:
1,69 km
Como o resultado é aproximado, a alternativa correta é a letra E.
Resposta Questão 3
Para solucionar esse problema, basta usar a lei dos senos, percebendo que 60° é oposto ao lado de 10 cm e que 45° é oposto ao lado cuja medida queremos descobrir.
Alternativa: A
Resposta Questão 4
Observe que x é oposto ao ângulo B. Para descobrir sua medida, basta fazer: 135 + 15 + B = 180. Nesse caso, B = 30°. Usando a lei dos cossenos, teremos:
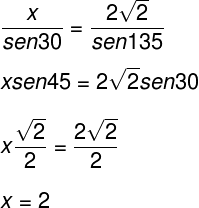
Alternativa: A




.jpg)