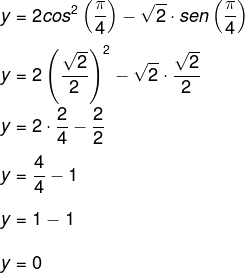Questão 1
Uma função trigonométrica possui lei de formação igual a f(x) = 2cos(x) – 1. O valor numérico dessa função quando x = π/3 é:
A) -2
B) -1
C) 0
D) 1
E) 2
Questão 2
Dada a função f(x) = 3sen(4x) + 6, com domínio e contradomínio nos números reais, podemos afirmar que o conjunto imagem dessa função é:
A) [-4, 4]
B) [-4, 6]
C) [6, 3]
D) [3, 9]
E) ]-∞, ∞[
Questão 3
Uma função de A → B possui lei de formação igual a:
![]()
Podemos afirmar que o menor valor que essa função pode ter assim é:
A) -2
B) -1
C) 0
D) 1
E) 2
Questão 4
Seja f(x) = 1 + 2sen(x), qual deve ser o valor de x, sabendo que ele é um ângulo do 1º quadrante, que faz com que f(x) = 2:
A) π
B) π/2
C) π/3
D) π/4
E) π/6
Questão 5
Analise as afirmativas a seguir sobre as funções trigonométricas:
I → A função tangente possui imagem no conjunto [-1, 1].
II → A função cosseno e a função seno são periódicas.
III → O conjunto imagem da função trigonométrica y = sen(x) + cos(x) é [-1, 1].
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Todas as afirmativas são verdadeiras.
Questão 6
(Enem) Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), produtos sazonais são aqueles que apresentam ciclos bem definidos de produção, consumo e preço. Resumidamente, existem épocas do ano em que a sua disponibilidade nos mercados varejistas ora é escassa, com preços elevados, ora é abundante, com preços mais baixos, o que ocorre no mês de produção máxima da safra.
A partir de uma série histórica, observou-se que o preço P, em reais, do quilograma de certo produto sazonal pode ser descrito pela função
![]()
onde x representa o mês do ano, sendo x = 1 associado ao mês de janeiro, x = 2 ao mês de fevereiro, e assim sucessivamente, até x = 12 associado ao mês de dezembro.
Na safra, o mês de produção máxima desse produto é
A) janeiro.
B) abril.
C) junho.
D) julho.
E) outubro.
Questão 7
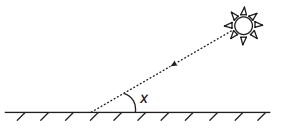
(Enem 2017) Raios de luz solar estão atingindo a superfície de um lago formando um ângulo x com a sua superfície, conforme indica a figura.
Em determinadas condições, pode-se supor que a intensidade luminosa desses raios, na superfície do lago, seja dada aproximadamente por I(x) = k · sen(x), sendo k uma constante, e supondo-se que X está entre 0° e 90º.
Quando x = 30º, a intensidade luminosa se reduz à qual percentual de seu valor máximo?
A) 33%
B) 50%
C) 57%
D) 70%
E) 86%
Questão 8
(Enem 2018) Em 2014 foi inaugurada a maior roda-gigante do mundo, a High Roller, situada em Las Vegas. A figura representa um esboço dessa roda-gigante, no qual o ponto A representa uma de suas cadeiras:
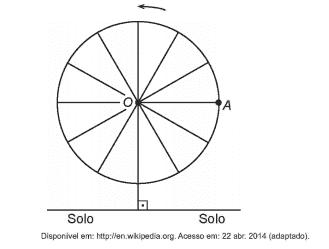
A partir da posição indicada, em que o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função que descreve a altura do ponto A, em relação ao solo, em função de t. Após duas voltas completas, f tem o seguinte gráfico:
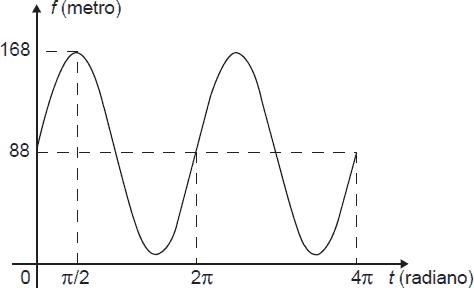
A expressão da função altura é dada por:
A) f(t) = 80sen(t) + 88
B) f(t) = 80cos(t) + 88
C) f(t) = 88cos(t) + 168
D) f(t) = 168sen(t) + 88cos(t)
E) f(t) = 88sen(t) + 168cos(t)
Questão 9
(Furb) Considere o gráfico a seguir:
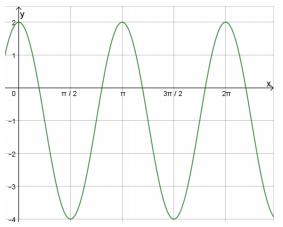
Pode-se afirmar que a função que está representada nesse gráfico é:
A) y = 3cos(2x) – 1
B) y = cos(2x) + 2
C) y = 2cos(2x) – 4
D) y = 3cos(x/2) – 1
E) y = 2cos(x/2) – 4
Questão 10
Conhecendo a função trigonométrica y = 2cos²(x) – √2sen(x), o valor da função quando x = π/4 é:
A) -2
B) -1
C) 0
D) 1
E) 2
Questão 11
Durante a análise de uma função, Kárita encontrou uma função trigonométrica, e ficou em dúvida entre as funções f(x) = sen(x); f(x) = cos(x); e f(x) = tg(x).
I → A função possui imagem [-1, 1].
II → A função é trigonométrica e possui período igual a 2π.
III → O valor numérico da função f(π/2) = 1.
A função descrita por ela é:
A) uma função seno
B) uma função cosseno
C) uma função tangente
D) uma função cotangente
E) uma função exponencial
Questão 12
Das alternativas a seguir, marque aquela que possui a lei de formação de uma função trigonométrica:
A) f(x) = logx
B) f(x) = ex
C) f(x) = 2cos(x) – 4
D) f(x) = 4x + senπ
E) f(x) = 2x + 3
Resposta Questão 1
Alternativa C
Queremos o valor de f(x) para x = π/3, então, temos que:
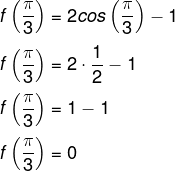
Resposta Questão 2
Alternativa D
Sabemos que sen(x) está sempre entre -1 e 1, então, para calcular o mínimo da função, temos que sen(x) = -1.
f(x) = 3 · (-1) + 6
f(x) = -3 + 6
f(x) = 3
Agora, o máximo da função é quando sen(x) = 1:
f(x) = 3 · 1 + 6
f(x) = 3 + 6
f(x) = 9
Resposta Questão 3
Alternativa D
Analisando o denominador, sabemos que ele sempre será positivo, já que cos(x) será sempre menor que 1.
Então, para encontrar o menor valor possível da função, vamos dividir 2 pelo maior número possível.
Nesse caso, admitindo cos(x) = -1, temos que:
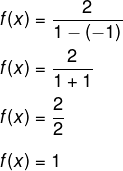
Assim, o menor valor possível para essa função é 1.
Resposta Questão 4
Alternativa E
Dada a função f(x) 1 + 2sen(x), sabemos que:
1 + 2sen(x) = 2
2sen(x) = 2 – 1
2sen(x) = 1
sen(x) = 1/2
Queremos encontrar o ângulo do 1º quadrante cujo o valor de seu seno é ½. Nesse caso, trata-se de um ângulo notável que é o ângulo de 30º, que, em radianos, corresponde ao arco π/6.
Resposta Questão 5
Alternativa B
-
Falsa. Diferentemente das funções seno e cosseno, a imagem da função tangente não é limitada entre -1 e 1, podendo ser qualquer número real.
-
Verdadeira. Sabemos que a função cosseno é periódica, pois ela possui período igual a 2π.
-
Falsa. O maior valor da imagem da função é quando sen(x) = 1, ou seja, y = 1 + 3 = 4. O menor valor da imagem da função é quando sen(x) = -1, ou seja, y = -1 + 3 = 2. Assim, a imagem da função seria o conjunto [2, 4].
Resposta Questão 6
Alternativa D
A safra tem seu valor máximo quando o preço é o mínimo possível, e, para isso, o menor valor que o cosseno pode assumir é -1. Ainda, o ângulo que faz com que cos(a) = -1 é a = π, então, temos que:
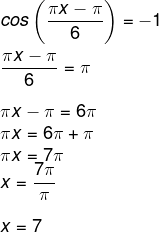
Sabemos que o mês 7 é o mês de julho.
Resposta Questão 7
Alternativa B
No intervalo de 0º a 90º, a função seno tem seu maior valor quando x = 90º, então, temos que:
i = k · sen(90º)
i = k · 1
i = k
Agora, quando x = 30º, temos que:
i = k · sen(30º)
i = k · 1/2
i = k/2
Como, com 30º, a intensidade é a metade de k, então ela se reduziu a 50% do seu valor máximo.
Resposta Questão 8
Alternativa A
Sabemos que f(π/2) = 168, que é o máximo da função. A função trigonométrica que tem esse comportamento com máximo em π/2 é a função seno, logo, a função possui lei de formação igual a:
f(t) = X + Y sen(t)
Quando t = 0 e f(t) = 88:
f(0) = X + Ysen(0)
88 = X + Y · 0
88 = X
Conhecendo o valor de X, note que f(π/2) = 168:
f(π/2) = 88 + Ysen(π/2)
168 = 88 + Y · 1
168 – 88 = Y
80 = Y
Então, a lei de formação da função altura é f(t) = 80 + 88sen(t).
Resposta Questão 9
Alternativa A
Analisando a função, sabemos que:
y = Acos(kx) + B
Sabemos que o ponto (0, 2) pertence ao gráfico, então, temos que:
2 = Acos(k0) + B
2 = Acos(0) + B
2 = A + B
Sabemos que o menor valor que cos(kx) pode assumir é -1, e, quando cos(kx) = -1, temos que f(x) = -4.
-4 = A (-1) + B
-4 = -A + B
Então, temos duas equações:
A + B = 2
-A + B = -4
Realizando a soma dessas equações, temos que:
0A + 2B = -2
2B = -2
B = -2 : 2
B = -1
Como A + B = 2 e B = -1, então, temos que:
A + (-1) = 2
A – 1 = 2
A = 2 + 1
A = 3
Então, a lei de formação é:
y = 3cos(kx) – 1
Por fim, para encontrar o valor de k, temos que x = π, então, y = 2, logo, temos que:
2 = 3cos(kπ) – 1
2 + 1 = 3cos(kπ)
3 = 3cos(kπ)
3 : 3 = cos(kπ)
1 = cos(kπ)
Sabemos que cos(2π) = 1, então, temos que:
kπ = 2π
k = 2
Assim, a lei de formação da função é:
y = 3cos(2x) – 1
Resposta Questão 11
Alternativa A
Analisando as informações dadas, sabemos que as funções trigonométricas que satisfazem a afirmativa I e II são a seno e a cosseno, pois ambas são periódicas e também possuem imagem entre [-1, 1].
Para diferenciar entre as duas funções, utilizamos a afirmativa III. A função trigonométrica que possui valor f(π/2) = 1 é a função f(x) = sen(x).
Resposta Questão 12
Alternativa C
A alternativa que contém uma função trigonométrica é a C, pois note que somente nela há uma razão trigonométrica cujo o ângulo é a variável x.