Questão 2
Quais são as imagens da função y = √(x2 – 8x + 16) para os elementos do domínio x = 2, x = 3 e x = 4?
Questão 3
(FAMERP SP/2016)
A figura representa o desenho da arcada dentária de um animal, feito no plano cartesiano ortogonal em escala linear.
.jpg)
Sabendo que as posições dos centros dos dentes destacados em cinza nessa arcada são modeladas nesse plano por meio da função quadrática y = ax2 + b, então a + b é igual a
a) 8,5.
b) 9,2.
c) 9,5.
d) 10,2.
e) 9,0.
Questão 4
(FGV /2016)
A área de um segmento parabólico, sombreado na figura a seguir, pode ser calculada por meio da fórmula seguinte, sendo V o vértice da parábola.
A = 2·PV·AB
3
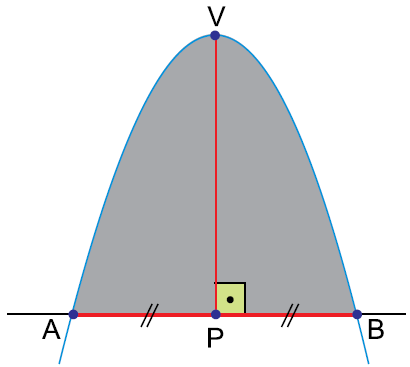
Sendo b um número real positivo, a parábola de equação y = –0,5x2 + bx determina, com o eixo x do plano cartesiano, um segmento parabólico de área igual a 18. Sendo assim, b é igual a:
a) 2.
b) 3.
c) 4.
d) 5.
e) 6.
Resposta Questão 1
Sabendo que o radicando deve ser sempre um número não negativo, a função acima está definida para todo x real tal que x2 – 8x + 16 ≥ 0. Logo:
x2 – 8x + 16 ≥ 0
(x – 4)2 ≥ 0
x – 4 ≥ 0
x ≥ 4
O domínio da função y = √(x2 – 8x + 16) é Df = {x.jpg) R: x ≥ 4 }
R: x ≥ 4 }
Resposta Questão 2
y = √(x2 – 8x + 16)
f(x) = √(x2 – 8x + 16)
f(2) = √(22 – 8·2 + 16)
f(2) = √(4 – 16 + 16)
f(2) = √4
f(2) = 2
f(3) = √(32 – 8·3 + 16)
f(3) = √(9 – 24 + 16)
f(3) = √(9 – 8)
f(3) = √1
f(3) = 1
f(4) = √(42 – 8·4 + 16)
f(4) = √(16 – 32 + 16)
f(4) = √(16 – 16)
f(4) = √0
f(4) = 0
Resposta Questão 3
Para encontrar os valores de a e b, é necessário construir um sistema de duas equações e duas variáveis. Para tanto, escolha dois pontos pertencentes à função, a partir dos quais seja possível obter os valores das coordenadas x e y, e substitua na função. Observe:
Os pontos escolhidos são (4,2) e (2,8).
Primeira equação:
y = ax2 + b
2 = a42 + b
2 = 16a + b
Segunda equação:
y = ax2 + b
8 = a22 + b
8 = 4a + b
Sistema:
2 = 16a + b
8 = 4a + b
Subtraindo a primeira equação pela segunda, obtemos:
–6 = 12a
a = –6
12
a = –1
2
Substituindo o valor de a na segunda equação, obtemos:
8 = 4a + b
8 = 4·(–1) + b
2
8 = –2 + b
b = 8 + 2
b = 10
Logo, a soma a + b é:
a + b = –1 + 10 = – 0,5 + 10 = 9,5
2
Alternativa C.
Resposta Questão 4
Para resolver esse problema, é preciso encontrar as raízes da função da parábola y = –0,5x2 + bx. Essas raízes são os pontos A e B, e a distância entre elas é o comprimento AB. Para tanto, colocaremos y = 0 e x em evidência:
0 = –0,5x2 + bx
0 = x(-0,5x + b)
x = 0 ou
-0,5x + b = 0
0,5x = b
x = 2b
Portanto, como x = 0 ou x = 2b, teremos AB = 2b. O segundo passo é descobrir o comprimento PV, dado por Yv (coordenada y do vértice da parábola).
PV = -Δ
4a
PV = b2 – 4·(– 0,5)·0
4·(– 0,5)
PV = b2
2
Agora basta calcular o valor de b utilizando a fórmula da área da parábola:
A = 2AB·PV
3
18 = 2AB·PV
3
27 = b3
b = 3
Alternativa B.



