Questão 1
Dada a função f(x) = x³ + 3x² – 2x – 9, o valor de f(2) – f( – 3) é:
A) – 3
B) 2
C) 3
D) 7
E) 10
Questão 2
Uma função polinomial possui a lei de formação f(x) = 3x5 + 2x³ – 2x + x – 8. Analisando essa função, podemos afirmar que ela possui grau:
A) 3
B) 4
C) 5
D) 6
E) 7
Questão 3
Sobre as funções, julgue as afirmativas a seguir:
I – O gráfico de uma função polinomial do 1º grau é sempre uma reta.
II – Toda função é polinomial, sendo variável apenas o grau da função.
III – A função f(x) = 3x³ + 2x4 – 3x + 8 possui grau 3.
Analisando as afirmativas, podemos afirmar que:
A) Somente I é verdadeira.
B) Somente II é verdadeira.
C) Somente III é verdadeira.
D) Todas são falsas.
Questão 4
O valor da corrida de um taxista é calculado por meio da função que relaciona a distância percorrida em quilômetros e a taxa fixa de R$ 5,50, conhecida como bandeira fixa. Sabendo que o valor por km rodado é de R$ 2,75, a quantia paga pelo cliente após rodar 7 km é de:
A) R$ 22,00.
B) R$ 24,75.
C) R$ 26,50.
D) R$ 27,25.
E) R$ 52,50.
Questão 5
(Enem 2010 – PPL) Em fevereiro, o governo da Cidade do México, metrópole com uma das maiores frotas de automóveis do mundo, passou a oferecer à população bicicletas como opção de transporte. Por uma anuidade de 24 dólares, os usuários têm direito a 30 minutos de uso livre por dia. O ciclista pode retirar em uma estação e devolver em qualquer outra e, se quiser estender a pedalada, paga 3 dólares por hora extra.
Revista Exame. 21 abr. 2010.
A expressão que relaciona o valor f pago pela utilização da bicicleta por um ano, quando se utilizam x horas extras nesse período é
A) f(x) = 3x
B) f(x) = 24
C) f(x) = 27
D) f(x) = 3x + 24
E) f(x) = 24x + 3
Questão 6
O valor de m que faz com que a função f(x) = (m² – 25) x3 + (m + 5)x² + mx + 3 seja uma função do 1º grau é:
A) 0
B) 3
C) 4
D) 5
E) – 5
Questão 7
(Enem 2016) Para evitar uma epidemia, a Secretaria de Saúde de uma cidade dedetizou todos os bairros, de modo a evitar a proliferação do mosquito da dengue. Sabe-se que o número f de infectados é dado pela função f(t) = -2t² + 120t (em que t é expresso em dia e t = 0 é o dia anterior à primeira infecção) e que tal expressão é válida para os 60 primeiros dias da epidemia.
A Secretaria de Saúde decidiu que uma segunda dedetização deveria ser feita no dia em que o número de infectados chegasse à marca de 1600 pessoas, e uma segunda dedetização precisou acontecer.
A segunda dedetização começou no
A) 19º dia.
B) 20º dia.
C) 29º dia.
D) 30º dia.
E) 60º dia.
Questão 8
(Enem 2009) Um grupo de 50 pessoas fez um orçamento inicial para organizar uma festa, que seria dividido entre elas em cotas iguais. Verificou-se ao final que, para arcar com todas as despesas, faltavam R$ 510,00, e que 5 novas pessoas haviam ingressado no grupo. No acerto foi decidido que a despesa total seria dividida em partes iguais pelas 55 pessoas. Quem não havia ainda contribuído pagaria a sua parte, e cada uma das 50 pessoas do grupo inicial deveria contribuir com mais R$ 7,00.
De acordo com essas informações, qual foi o valor da cota calculada no acerto final para cada uma das 55 pessoas?
A) R$ 14,00.
B) R$ 17,00.
C) R$ 22,00.
D) R$ 32,00.
E) R$ 57,00.
Questão 9
(UCS 2014 — adaptada) O salário mensal de um vendedor é de R$ 750,00 fixos mais 2,5% sobre o valor total, em reais, das vendas que ele efetuar durante o mês. Em um mês em que suas vendas totalizarem x reais, o salário do vendedor será dado pela expressão:
A) S(x) = 750 + 2,5x
B) S(x) = 750 + 0,25x
C) S(x) = 750,25x
D) S(x) = 750 · (0,25x)
E) S(x) = 750 + 0,025x
Questão 10
Sobre o gráfico de uma função polinomial, julgue as afirmativas a seguir:
I → O gráfico de uma função afim é sempre uma reta.
II → O gráfico de funções polinomiais são retas ou uma parábola.
III → O gráfico de uma função do 2º grau é sempre cúbico.
Está correta:
A) Somente a afirmativa I.
B) Somente a afirmativa II.
C) Somente a afirmativa III.
D) Nenhuma afirmativa.
Questão 11
Dadas as funções a seguir, assinale aquela que corresponde a uma função polinomial:
A) f(x) = 2x + 5
B) f(x) = cos (x) + 3
C) f(x) = 3 – x
D) f(x) = √x + 3
E) f(x) = logx + 2
Questão 12
Uma loja de calçados recebe um lucro de 40% sobre a venda de qualquer par. Ou seja, a função do lucro é: L(x) = 0,4x, em que x é o valor dos sapatos. Dado o valor do produto, a loja vende os sapatos pelo dobro do valor gasto mais um adicional de R$ 15,00 — isto é, V(c) = 2c + 15, em que c é o custo para produzir o produto. A função que expressa o lucro L em função do valor do custo c é:
A) L(c) = 0,4c + 8
B) L(c) = 0,8c + 15
C) L(c) = 0,6c + 3
D) L(c) = 0,03c – 3
E) L(c) = 0,2c +4
Resposta Questão 1
Alternativa E
Calculando f(2), temos que:
f(2) = 2³ + 3 · 2² – 2 · 2 – 9
f(2) = 8 + 3 · 4 – 4 – 9
f(2) = 8 + 12 – 4 – 9
f(2) = 20 – 13
f(2) = 7
Calculando f(– 3):
f(– 3) = (– 3)³ + 3 · (– 3)² – 2 · (– 3) – 9
f(– 3) = – 27 + 27 + 6 – 9
f(– 3) = – 3
Então, temos que f(2) – f(– 3) = 7 – (– 3) = 7 + 3 = 10.
Resposta Questão 2
Alternativa C
O grau da função é igual ao maior expoente da variável. Note que, nesse caso, o maior expoente é 5. Logo, essa função polinomial possui grau 5.
Resposta Questão 3
Alternativa A
Analisando as afirmativas, percebemos que:
I → Verdadeira
O gráfico de uma função do primeiro grau é sempre uma reta.
II → Falsa
Existem outras funções, que não são polinomiais.
III → Falsa
O maior expoente da função é 4, logo ela é do 4º grau.
Resposta Questão 4
Alternativa B
Primeiro vamos descrever a função que relaciona o valor pago V pela quantidade de km percorridos. Sabemos que são cobrados R$ 2,75 por km rodado, além da taxa fixa de R$ 5,50.
V(x) = 2,75x + 5,50
Queremos saber, então, o valor numérico para x = 7
V(7) = 2,75 · 7 + 5,50
V(7) = 19.25 + 5,50
V(7) = 24,75
Resposta Questão 5
Alternativa D
Sabemos que há um custo fixo de 24 dólares. Além disso, é cobrado por x horas um valor de 3 dólares, sendo x um número real que representa o número de horas extras. Então, podemos descrever essa função como:
f(x) = 3x + 24
Resposta Questão 6
Alternativa E
Para que essa função seja do 1º grau, temos que m² – 25 = 0 e que m + 5 = 0.
Resolvendo a primeira, temos que:
m² – 25 = 0
m² = 25
m = ±√25
m = ± 5
Agora, resolvendo a segunda, temos que:
m + 5 = 0
m = – 5
Logo, o único valor que faz com que m² – 25 e m + 5 sejam igual a zero simultaneamente é m = – 5.
Resposta Questão 7
Alternativa B
Queremos o valor de t para que – 2t² + 120t = 1600
Aplicando a equação do 2º grau, temos que:
– 2t² + 120t – 1600 = 0
a = – 2; b = 120 e c = – 1600
∆ = ( – 120)² – 4 · 2 · 160
∆ = 14400 – 12800
∆ = 1600
Agora, aplicando a fórmula de Bhaskara:
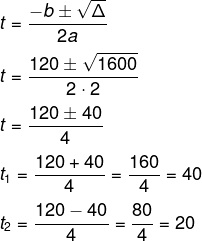
Então, a dedetização ocorreu no 20º dia.
Resposta Questão 8
Alternativa D
Sendo x o valor pago por pessoa, a despesa pode ser representada por D(x) = 55x. Inicialmente, 50 pessoas pagariam x – 7, e faltariam 510 reais para pagar a despesa. Ou seja:
D(x) = 50 (x – 7) + 510
Igualando as duas equações, temos que:
55x = 50 (x – 7) + 510
55x = 50x – 350 + 510
55x – 50x = 160
5x = 160
x = 160 : 5
x = 32
Logo, cada um pagará 32 reais.
Resposta Questão 9
Alternativa E
Para calcular 2,5% de x, basta escrever a porcentagem na forma decimal, ou seja, 0,025x. Além disso, o salário possui uma parte fixa de 750 reais, então a função que descreve essa situação é:
S(x) = 750 + 0,025x
Resposta Questão 10
Alternativa A
I → Verdadeira
Sabemos que o gráfico de uma função polinomial do 1º grau, conhecida também como uma função afim, é sempre uma reta.
II → Falsa
O gráfico depende do grau da função. Para cada grau, há um tipo de gráfico.
III → Falsa
A função do 2º grau tem como gráfico uma parábola.
Resposta Questão 11
Alternativa C
Analisando as afirmativas, vemos que a única que corresponde a uma função polinomial é a alternativa C.
f(x) = 3 – x
Resposta Questão 12
Alternativa B
Temos que L(x) = 0,4x. Na função do lucro, vamos substituir x por 2c + 15. Então, temos que:
L(c) = 0,4 (2c + 15)
L(c) = 0,8c + 6



