Questão 1
(Enem 2015) A figura representa a vista superior de uma bola de futebol americano, cuja forma é um elipsoide obtido pela rotação de uma elipse em torno do eixo das abscissas. Os valores a e b são, respectivamente, a metade do seu comprimento horizontal e a metade do seu comprimento vertical. Para essa bola, a diferença entre os comprimentos horizontal e vertical é igual à metade do comprimento vertical.
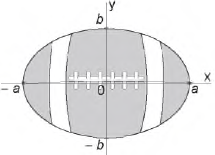
Considere que o volume aproximado dessa bola é dado por V = 4ab². O volume dessa bola, em função apenas de b, é dado por:
A) 8b³
B) 6b³
C) 5b³
D) 4b³
E) 2b³
Questão 2
A distância focal da elipse que passa pelos pontos A1(-6, 0), A2(6, 0) e B1(0, 10) e B2(0, -10) é de:
A) 6
B) 8
C) 10
D) 12
E) 16
Questão 3
As coordenadas do foco da elipse, que possui a equação a seguir, são:
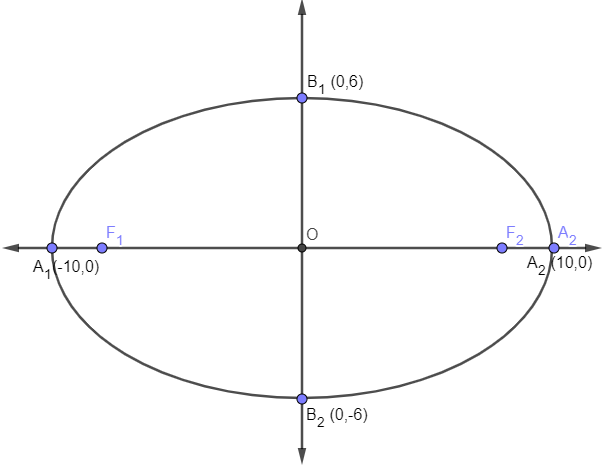
A) (0, 8) e (0, -8)
B) (4, 0) e (-4, 0)
C) (8, 0) e (-8, 0)
D) (4, 4) e (-4, 4)
E) (0, 4) e (4, 0)
Questão 4
Qual é a excentricidade da elipse 4x² + 25y² = 100 aproximadamente:
(Use √3 = 1,7 e √7 = 2,6)
A) 0,84
B) 1,13
C) 0,70
D) 0,88
E) 0,28
Questão 5
(UEL PR) Em uma praça dispõe-se de uma região retangular de 20 m de comprimento por 16 m de largura para construir um jardim. A exemplo de outros canteiros, este deverá ter a forma elíptica e estar inscrito nessa região retangular. Para aguá-lo, serão colocados dois aspersores nos pontos que correspondem aos focos da elipse. Qual será a distância entre os aspersores?
A) 4 m
B) 6 m
C) 8 m
D) 10 m
E) 12 m
Questão 6
A equação da elipse com o centro na origem do plano cartesiano e que passa pelos pontos A1(5, 0), A2 (-5, 0) e B2 (0, -4) é:
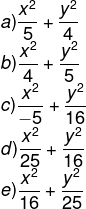
Questão 7
Uma elipse foi traçada no plano cartesiano a seguir:
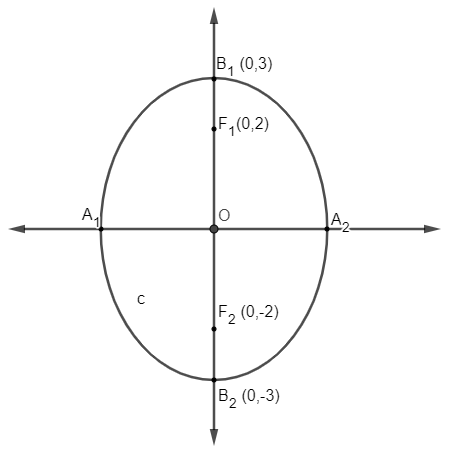
Na geometria analítica, é possível descrever essa elipse por meio de uma equação. Nesse caso, a equação da elipse seria:
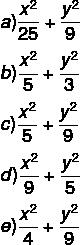
Questão 8
(Cesgranrio 2018) Uma câmara dos sussurros é um espaço em que, se duas pessoas estão nas posições especificadas como foco, elas podem falar entre si, mesmo sussurrando, a uma distância considerável. Isso porque os painéis colocados atrás delas são partes de uma mesma elipse cujos focos são as posições das cabeças das pessoas.
Na câmara de sussurros representada na Figura a seguir, a distância entre as duas pessoas é de 20 m, e a distância de cada pessoa até um vértice da elipse é de 2 m.
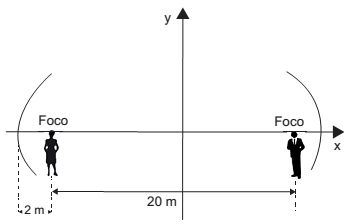
A equação da elipse que contém os painéis da câmara representada no sistema de eixos proposto na Figura é:
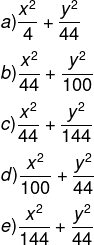
Questão 10
Uma elipse possui eixo maior contido no eixo Oy, seu centro é igual à origem do plano cartesiano, e a distância do eixo menor é 12. Além disso, a distância entre os focos é de 20 unidades. Sendo assim, a distância focal dessa elipse é de:
A) 4
B) 6
C) 10
D) 16
E) 15
Questão 11
Em uma casa, será feita uma área de lazer no formato de uma elipse, com eixo maior medindo 7 metros e eixo menor medindo 5 metros. Para planejar a execução e os gastos nesse projeto, é importante calcular a área da área de lazer, que será de: (Use π = 3)
A) 105 m²
B) 52,5 m²
C) 43,0 m²
D) 35,0 m²
E) 26,5 m²
Questão 12
Sabendo que a diferença entre o comprimento do eixo maior e o seu eixo focal é igual a 4 e que o eixo menor mede 8 unidades, então o comprimento do maior eixo é igual a:
A) 5
B) 10
C) 6
D) 12
E) 9
Resposta Questão 1
Alternativa B. Se a diferença entre o comprimento horizontal e o vertical é igual à metade do comprimento vertical, então, temos que:
2a – 2b = b
2a = b + 2b
2a = 3b
a = 3b/2
a = 1,5b
Assim, para calcular o volume, temos que:
V = 4ab²
V = 4 (1,5b)b²
V = 6b²
Resposta Questão 2
Alternativa E
Temos que b = 10 e a = 6, como b > a, então:
b² = a² + c²
10² = 6² + c²
100 = 36 + c²
100 – 36 = c²
64 = c²
c = √64
c = 8
Como a distância focal é 2c, então 2 · 8 = 16.
Resposta Questão 3
Alternativa C
Para encontrar os focos da elipse, basta utilizar o teorema de Pitágoras, pois temos que:
a² = b² + c²
10² = 6² + c²
100 = 36 + c²
100 – 36 = c²
c² = 64
c = √64
c = 8
Como os focos estão no eixo x, então, os pontos são (8, 0) e (-8, 0).
Resposta Questão 4
Alternativa D
Primeiro precisamos encontrar o valor de a e de b. Para isso, vamos passar o 100 dividindo cada um dos termos na equação:
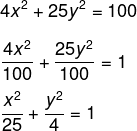
Então, temos que:
a² = 25 → a = √25 = 5
b² = 4 → b = √4 = 2
Para calcular a excentricidade, é necessário encontrar o valor de c. Como a > b, temos que:
a² = b² + c²
5² = 2² + c²
25 = 4 + c²
25 – 4 = c²
c² = 21
c = √21
Como conhecemos os valores de √3 e √7, então, temos que:
c = √21 = √7 · √3
c = 1,7 · 2,6
c = 4,42
A excentricidade é a razão entre c e a:
e = 4,42/5 = 0,884
Resposta Questão 5
Alternativa E
Para entender melhor o problema, vamos ilustrar a situação:
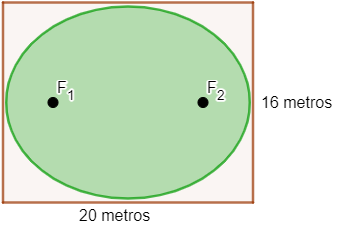
Queremos a distância focal igual a 2c.
Então, temos que o eixo maior mede 20 metros, e o menor, 16 metros:
2a = 20
a = 20/2 = 10
b = 16/2 = 8
Utilizando o teorema de Pitágoras:
a² = b² + c²
10² = 8² + c²
100 = 64 + c²
100 – 64 = c²
c² = 36
c = √36
c = 6
Logo, a distância focal é 2c = 2 · 6 = 12 metros.
Resposta Questão 6
Alternativa D
Nesse caso, temos que a = 5 e b = 4, então, a equação da elipse será:
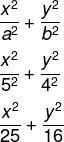
Resposta Questão 7
Alternativa C
Temos que c = 2 e b = 3. Note que o valor de a não foi dado. Como o foco está no eixo vertical, então:
b² = c² + a²
3² = 2² + a²
9 = 4 + a²
9 – 4 = a²
a² = 5
a = √5
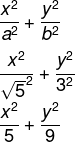
Resposta Questão 8
Alternativa E
Como a distância entre os focos é igual a 20 metros, então, 2c = 20 → c = 10.
Sabemos que o foco está a 2 metros da extremidade:
a = 10 + 2
a = 12
Conhecendo a e c, pelo teorema de Pitágoras, encontraremos o valor de b:
12² = c² + b²
12² = 10² + b²
144 = 10² + b²
144 – 100 = b²
b² = 44
b = √44
Então, temos que:
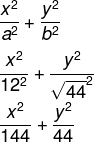
Resposta Questão 9
Alternativa A
Primeiro vamos dividir todos os termos por 36 na equação:
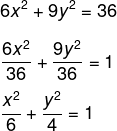
Então, temos que:
a² = 6 → a = √6
b² = 4 → b = √4 = 2
Para calcular a excentricidade, precisamos encontrar o valor de c, como a > b, temos que:
a² = b² + c²
√6² = 2² + c²
6 = 4 + c²
c² = 6 – 4
c = √2
Por fim, vamos calcular a excentricidade:
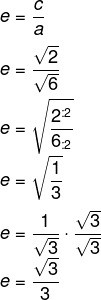
Resposta Questão 10
Alternativa D
O eixo maior é o eixo y, então:
2b = 20
b = 20/2
b = 10
2a = 12
a = 12/2
a = 6
Aplicando o teorema de Pitágoras:
b² = a² + c²
10² = 6² + c²
100 = 36+ c²
100 – 36 = c²
c² = 64
c = √64
c = 8
A distância focal é: 2c → 2 · 8 = 16
Resposta Questão 11
Alternativa E
A área da elipse é dada por: A = ab π
Como não foi definida a posição da elipse, e nesse caso ela é indiferente, faremos 2a como comprimento do eixo maior:
2a = 7
a = 7/2
a = 3,5
2b = 5
b = 5/2
b = 2,5
A = ab π
A = 3,5 · 2,5 · 3 = 26,5
Resposta Questão 12
Alternativa B
Suponha que o eixo maior seja o horizontal, então, 2a – 2c = 4. Se dividirmos por dois, temos que:
a – c = 2
a = 2 + c
Além disso, sabemos que:
2b = 8
b = 8/2
b = 4
Pela relação pitagórica, temos que:
a² = b² + c²
(2 + c)² = 4² + c²
4 + 4c + c² = 16 + c²
c² – c² + 4c = 16 – 4
4c = 12
c = 12/4
c = 3
Então, temos que:
a² = 4² + 3²
a² = 16 + 9
a² = 25
a = √25
a = 5
Então o comprimento do eixo maior é: 2a = 2 · 5 = 10



