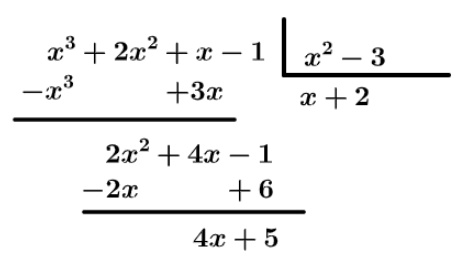Questão 1
O resto da divisão do polinômio \(x^2-x+6\) pelo polinômio \(x - 3\) é igual a:
A) x
B) -x
C) -2x + 6
D) 2x + 6
E) 0
Questão 2
Qual é o valor de n para que o polinômio x³ - 2x² + nx + 4 seja divisível por x – 2?
A) 4
B) 2
C) 0
D) – 2
E) – 4
Questão 3
A divisão do polinômio P(x) = 2x³ - 7x² + 4x + 1 pelo polinômio 2x² - 5x – 1 tem como quociente o polinômio:
A) - x + 1
B) x + 1
C) x – 1
D) 2x + 2
E) – 2x – 1
Questão 4
A divisão do polinômio P(x) pelo polinômio D(x) = x² + 2x – 5 gera como quociente o polinômio Q(x) = 3x – 1 e o resto R(x) = 5x + 2. Então, o polinômio P(x) é:
A) P(x) = 3x³ + 5x² - 12x + 5
B) P(x) = x³ + 5x² - 17x + 5
C) P(x) = 3x³ + 6x² - 15x + 7
D) P(x) = 2x³ - 4x² + 12x + 7
E) P(x) = 3x³ + 5x² - 12x + 7
Questão 5
Ao dividirmos o polinômio P(x) pelo polinômio D(x) = x² + 2x – 1, encontramos o quociente Q(x) = x + 2 e o resto R(x) = - 2. Então o valor de P(-1) é:
A) – 1
B) – 2
C) – 3
D) – 4
E) – 5
Questão 6
Quando simplificamos a expressão
\(\frac{4x^2 y^4+8xy^5-2xy+6x^4 y^2}{2xy}\)
encontramos como resposta o polinômio:
A) \(2xy^3+4y-1+3x^3 y\)
B) \(2x+4y+1+3x^3 y\)
C) \(xy^3+4y+3x^3 y\)
D) \(2y^3+4y+x^2 y\)
E) \( 2xy^3+4y-1+3x^3\)
Questão 7
Sobre a divisão de polinômios, julgue as afirmativas a seguir:
I. O resto na divisão entre polinômios sempre terá grau igual ou menor que o grau do divisor.
II. Quando a divisão de P(x) por D(x) é 0, podemos afirmar que P(x) não é divisível por D(x).
Marque a alternativa correta.
A) As duas afirmativas são verdadeiras.
B) Somente a afirmativa I é verdadeira.
C) Somente a afirmativa II é verdadeira.
D) As duas afirmativas são falsas.
Questão 8
O grau do resto da divisão do polinômio x² + 2x² + x – 1 pelo polinômio x² - 3 é:
A) 4
B) 3
C) 2
D) 1
E) 0
Questão 9
Dados os polinômios: P(x) = \(2x^5+8x^3-3x²\) e D(x) = \(2x^2\), o resultado dessa divisão possui grau igual a:
A) 5
B) 4
C) 3
D) 2
E) 1
Questão 10
Considerando os polinômios P(x) = 2x² + 3x – 1 e D(x) = 3x² + 4x – 5, P(2) : D(-2) é:
A) 10
B) – 12
C) 12
D) - 13
E) 13
Questão 11
Considere o polinômio P(x) = 3x² + 2x – k. O valor de k para que esse polinômio seja divisível por x – 1 é:
A) – 5
B) 5
C) 3
D) – 3
E) 2
Questão 12
(Vunesp) O polinômio P(x) = x3 – mx2 + n, em que m e n são constantes reais, é divisível pelo polinômio Q(x) = x2 – x – 3. Sabendo que P(3) = 0, a diferença n – m é igual a
A) – 3
B) – 2
C) 0
D) 5
E) 8
Resposta Questão 1
Alternativa E.
Calculando a divisão dos polinômios (soma algébrica de monômios), temos que:
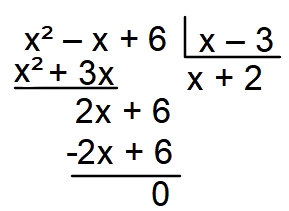
Então, o resto dessa divisão é igual a 0.
Resposta Questão 2
Alternativa D.
Se x³ - 2x² + nx + 4 é divisível por x -2, então, pelo teorema do resto do polinômio:
x – 2 = 0
x = 2
Substituindo x = 2 no dividendo:
\(2^3-2⋅2^2+n⋅2+4=0\)
\(8-8+2n+4=0\)
\(2n+4=0\)
\(2n=-4\)
\(n=\frac{-4}2\)
\(n=-2\)
Resposta Questão 4
Alternativa E.
Sabemos que:
P(x) = D(x) ⋅ Q(x) + R(x)
Logo, temos que:
P(x) = (x² + 2x – 5)(3x – 1) + (5x + 2)
P(x) = (3x³ + 6x² - 15x – x² – 2x + 5) + (5x + 2)
P(x) = (3x³ + 5x² - 17x + 5) + (5x + 2)
P(x) = 3x³ + 5x² - 12x + 7
Resposta Questão 5
Alternativa D.
Sabemos que:
P(x) = D(x) ⋅ Q(x) + R(x)
Então:
\(P(x) = (x² + 2x – 1) (x+2) + ( - 2) \)
Calculando x = - 1:
\(P(-1)=((-1)^2+2(-1)-1) (-1+2)-2\)
\(P(-1)=(1-2-1)⋅1-2\)
\(P(-1)=(1-3)⋅1-2\)
\(P(-1)=-2⋅1⋅-2\)
\(P(-1)=-2-2\)
\(P(-1)=-4\)
Resposta Questão 6
Alternativa A.
\(\frac{4x^2 y^4+8xy^5-2xy+6x^4 y^2}{2xy}\)
Dividiremos cada monômio (expressão algébrica composta por letras e números) por 2xy:
\(4x^2 y^4:2xy=2xy^3\)
\(8xy^5:2xy=4y^4\)
\(-2xy∶2xy = - 1\)
\(6x^4 y^2:2xy=3x^3 y\)
A solução é o polinômio:
\(2xy^3+4y-1+3x^3 y \)
Resposta Questão 7
Alternativa B.
I. O resto na divisão entre polinômios sempre terá grau menor que o grau do divisor. (verdadeira)
II. Quando a divisão de P(x) por D(x) é 0, podemos afirmar que P(x) não é divisível por D(x). (falsa)
Quando o resto da divisão é 0, significa que P(x) é divisível por D(x).
Resposta Questão 8
Alternativa D.
Calculando a divisão dos polinômios:
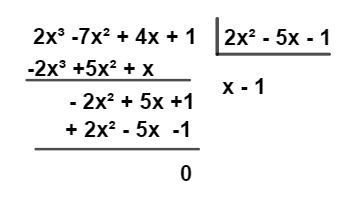
Note que 4x + 5 é um polinômio de grau 1.
Resposta Questão 9
Alternativa C.
Ao fazer a divisão de \(2x^5\) por \(2x^2\), encontramos o monômio x³, que será o maior expoente obtido na divisão, logo o grau do polinômio que resulta da divisão de P(x) por D(x) é igual a 3.
Resposta Questão 10
Alternativa D.
Calculando P(2):
\(P(2)=2⋅2^2+3⋅2-1\)
\(P(2)=8+6-1\)
\(P(2)=14-1\)
\(P(2)=13\)
Calculando D(-2):
\(D(-2)=3⋅(-2)^2+4⋅(-2)-5\)
\(D(-2)=3⋅4-8-5\)
\(D(2)=12-13\)
\(D(2)=-1\)
Então, temos a divisão:
\(P(2):D(2)=13:(-1)=-13\)
Resposta Questão 11
Alternativa B.
Pelo teorema do resto, temos que:
x – 1 = 0
x = 1
Substituindo 1 no valor de x em P(x) e igualando a zero:
\(0=3⋅1^2+2⋅1-k\)
\(0=3+2-k\)
\(k=3+2\)
\(k =5\)
Resposta Questão 12
Alternativa D.
Se P(3) = 0, então o polinômio D(x) = x – 3 divide P(x). Como o resto da divisão de P(x) por Q(x) é zero, temos que:
P(x) = Q(x)\(⋅D(x)\)
Logo:
P(x) = (x² - x – 3) ( x – 3)
P(x) = x³ - x² - 3x – 3x² +3x + 9
P(x) = x³ - 4x² + 9
Note, então, que:
x³ - mx² + n = x³ - 4 x² + 9
Igualando m ao coeficiente de x²:
- m = - 4
m = 4
Igualando n ao termo independente:
n = 9
A diferença n – m = 9 – 4 = 5.