Questão 1
O desvio-padrão do conjunto {1, 2, 3, 6} é, aproximadamente,
A) 1,8
B) 1,9
C) 2,0
D) 2,1
E) 2,2
Questão 2
Durante a coleta de dados de um determinado conjunto, percebeu-se que todos os elementos do conjunto possuíam o mesmo valor. Nessas condições, podemos afirmar que o desvio-padrão desse conjunto será:
A) 1
B) 0
C) – 1
D) 0,5
E) – 0,5
Questão 3
Em um conjunto de idades foi calculado o desvio-padrão, igual a 2. Nessas condições, podemos afirmar que o valor da variância desse conjunto é:
A) 1,0
B) 1,4
C) 3,0
D) 4,0
E) 8,0
Questão 4
A temperatura máxima de uma cidade foi registrada durante duas semanas:
|
|
Segunda |
Terça |
Quarta |
Quinta |
Sexta |
Sábado |
Domingo |
Média |
σ |
|
Primeira semana |
27° |
32° |
31° |
30° |
29° |
30° |
31° |
30° |
1,51 |
|
Segunda semana |
25° |
30° |
32° |
27° |
29° |
28° |
32° |
29° |
2,39 |
Analisando os dados, podemos afirmar que a semana em que houve maior variação de temperatura foi:
A) a primeira semana, pois a sua média é maior do que a da segunda semana.
B) a primeira semana, pois o seu desvio-padrão é menor do que o da segunda semana.
C) a segunda semana, pois a sua média é menor do que a da primeira semana.
D) a segunda semana, pois o seu desvio-padrão é maior do que o da primeira semana.
Questão 5
Ao analisar o conjunto A e o conjunto B, percebeu-se que o conjunto A possui desvio-padrão igual a 2,1; já o conjunto B possui desvio-padrão igual a 1,2. Analisando esses desvios-padrões, podemos concluir que:
A) a média do conjunto A é maior que a média do conjunto B.
B) a média do conjunto B é maior que a média do conjunto A.
C) o conjunto A possui elementos mais regulares que o conjunto B.
D) o conjunto A possui elementos menos regulares que o conjunto B.
E) a variância dos conjuntos é a mesma.
Questão 6
Durante uma competição de salto a distância, os atletas faziam 3 saltos, e a média desses saltos era calculada. Para vencer, o atleta deveria atingir a maior média. Em caso de empate entre as médias, o atleta que tivesse saltos mais regulares acaba levando o prêmio.
Na tabela seguir, temos os resultados de cada um dos atletas em metros:
|
Atleta |
1º salto |
2º salto |
3º salto |
Média |
Desvio padrão |
|
Caio |
5,2 m |
5,8 m |
6,4 m |
5,8 m |
0,49 |
|
Hélio |
5,0 m |
4,5 m |
6,1 m |
5,2 m |
0,67 |
|
Nicolas |
5,7 m |
5,7 m |
5,7 m |
5,7 m |
0,00 |
|
Heitor |
5,8 m |
6,0 m |
5,6 m |
5,8 m |
0,16 |
|
Marcelo |
5,4 m |
5,3 m |
5,5 m |
5,4 m |
0,08 |
Analisando os dados, podemos afirmar que o vencedor da competição foi:
A) Caio
B) Hélio
C) Nicolas
D) Heitor
E) Marcelo
Questão 7
As notas obtidas em uma prova da universidade na disciplina de Cálculo foram:
|
Aluno |
Nota |
|
Kárita |
10,0 |
|
Júlia |
9,8 |
|
Natália |
8,2 |
|
Thiago |
7,6 |
|
Marina |
7,4 |
|
Mariana |
7,0 |
|
Lara |
6,5 |
|
Gabriela |
6,5 |
|
Pedro |
5,3 |
|
Raul |
4,7 |
Analisando a tabela, nota-se que o desvio-padrão dessas notas é igual a, aproximadamente,
A) 1,58
B) 1,60
C) 1,63
D) 1,68
E) 1,72
Questão 8
No conjunto a seguir temos o peso de 8 pessoas: 50 kg, 75 kg, 88kg, 62kg, 70kg, 80kg, 55 kg e 88kg. O desvio-padrão desses pesos é igual a, aproximadamente,
A) 17,0
B) 16,2
C) 14,4
D) 13,6
E) 12,8
Questão 9
(Enem 2012) Um produtor de café irrigado em Minas Gerais recebeu um relatório de consultoria estatística, constando, entre outras informações, o desvio-padrão das produções de uma safra dos talhões de sua propriedade. Os talhões têm a mesma área de 30.000 m², e o valor obtido para o desvio-padrão foi de 90 kg/talhão. O produtor deve apresentar as informações sobre a produção e a variância dessas produções em sacas de 60 kg por hectare (10.000 m²).
A variância das produções dos talhões expressa em (sacas/hectare)² é
A) 20,25.
B) 4,50.
C) 0,71.
D) 0,50.
E) 0,25.
Questão 10
(Enem 2019 PPL) Um fiscal de certa empresa de ônibus registra o tempo, em minuto, que um motorista novato gasta para completar certo percurso. No Quadro 1 figuram os tempos gastos pelo motorista ao realizar o mesmo percurso sete vezes. O Quadro 2 apresenta uma classificação para a variabilidade do tempo, segundo o valor do desvio-padrão.
- Quadro 1:

- Quadro 2:
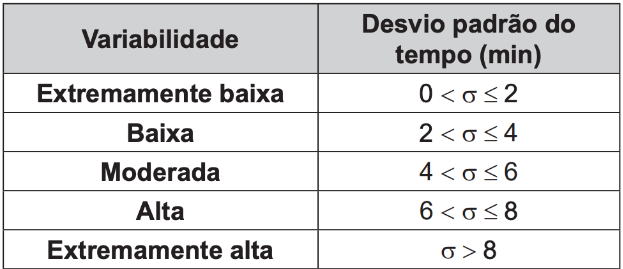
Com base nas informações apresentadas nos quadros, a variabilidade do tempo é
A) extremamente baixa.
B) baixa.
C) moderada.
D) alta.
E) extremamente alta.
Questão 11
(Enem 2010) Marco e Paulo foram classificados em um concurso. Para classificação no concurso, o candidato deveria obter média aritmética na pontuação igual ou superior a 14. Em caso de empate na média, o desempate seria em favor da pontuação mais regular. No quadro a seguir são apresentados os pontos obtidos nas provas de Matemática, Português e Conhecimentos Gerais, a média, a mediana e o desvio-padrão dos dois candidatos.
Dados dos candidatos no concurso:

O candidato com pontuação mais regular, portanto mais bem classificado no concurso, é
A) Marco, pois a média e a mediana são iguais.
B) Marco, pois obteve o menor desvio-padrão.
C) Paulo, pois obteve a maior pontuação da tabela, 19 em Português.
D) Paulo, pois obteve a maior mediana.
E) Paulo, pois obteve o maior desvio-padrão.
Questão 12
(IBFC 2022) O valor numérico da variância em uma distribuição X é igual a 0,81, e o valor numérico da variância em uma distribuição Y é igual a 0,64.
Nessas condições, é correto afirmar que:
A) o desvio-padrão da distribuição Y é maior que o desvio-padrão da distribuição X.
B) o desvio-padrão da distribuição Y é menor que o desvio-padrão da distribuição X.
C) a diferença entre os desvios-padrões das duas distribuições é igual a 0,17.
D) o desvio-padrão da distribuição X é igual a 0,09.
E) o desvio-padrão da distribuição Y é menor que 0,07.
Resposta Questão 1
Alternativa B
Calculando o desvio-padrão começando pela média, temos que:
\(\bar{x}=\frac{1+2+3+6}4=\frac{12}4=3\)
Sabendo que a média é 3:
(1 – 3)² = 4
(2 – 3)² = 1
(3 – 3)² = 0
(6 – 3)² = 9
Calculando a variância, que é a média dos resultados anteriores:
\(V=\frac{4+1+0+9}4=\frac{14}4=3,5\)
Por fim, o desvio-padrão será a raiz quadrada desse número, então:
\(D_p=\sqrt{3,5}≈1,87\)
Sabemos que 1,87 é aproximadamente 1,9.
Resposta Questão 2
Alternativa B
Quando todos os elementos do conjunto possuem o mesmo valor, não há dispersão entre os dados do conjunto, logo qualquer medida de dispersão desse conjunto será igual a 0, inclusive o desvio-padrão.
Resposta Questão 3
Alternativa D
Sabemos que o desvio-padrão é igual à raiz quadrada da variância, logo a variância é o quadrado do desvio-padrão:
\(V=D_p^2\)
\(V=2^2\)
\(V=4 \)
Resposta Questão 4
Alternativa D
A segunda semana foi a que teve maior variação, pois o seu desvio-padrão é maior.
Resposta Questão 5
Alternativa D
Podemos observar que o conjunto A possui maior desvio-padrão, logo eles possuem elementos que são menos regulares do que o conjunto B.
Resposta Questão 6
Alternativa D
Analisando os dados, podemos observar que há dois atletas que tiveram média maior, de 5,8 m — são eles Heitor e Caio. Como o vencedor é o atleta mais regular, então trata-se do que possui menor desvio-padrão; no caso, Heitor.
Resposta Questão 7
Alternativa C
Calculando a média, temos que:
\(\bar{x}=\frac{10,0+9,8+8,2+7,6+7,4+7,0+6,5+6,5+5,3+4,7}{10}=\frac{73}{10}=7,3\)
Agora, calculando a diferença entre os valores do conjunto e a média e elevando ao quadrado:
(10 – 7,3)² = 7,29
(9,8 – 7,3)² = 6,25
(8,2 – 7,3)² = 0,81
(7,6 – 7,3)² = 0,09
(7,4 – 7,3)² = 0,01
(7,0 – 7,3)² = 0,09
(6,5 – 7,3)² = 0,64
(6,5 – 7,3)² = 0,64
(5,3 – 7,3)² = 4,00
(4,7 – 7,3)² = 6,76
Calculando a média entre os resultados encontrados:
\(V=\frac{7,29+6,25+0,81+0,09+0,01+0,09+0,64+0,64+4,00+6,76}{10}=\frac{26,58}{10}=2,658\)
Por fim, calcularemos a raiz quadrada:
\(D_p=\sqrt{2,658}≈1,63\)
Resposta Questão 8
Alternativa D
Calculando a média, temos que:
\(\bar{x}=\frac{50+75+88+62+70+81+55+88}8=\frac{568}8=71\)
Sabendo que a média é 50:
(50 – 71)² = 441
(75 – 71)² = 16
(88 – 71)² = 289
(62 – 71)² = 81
(70 – 71)² = 1
(81 – 71)² = 100
(55 – 71)² = 256
(88 – 71)² = 289
Calculando o desvio-padrão:
\(D_p=\sqrt{\frac{441+16+289+81+1+100+256+289}8}\)
\(D_p=\sqrt{\frac{1473}{8}}\)
\(D_p=\sqrt{184,125}\)
\(Dp≈13,6\)
Resposta Questão 9
Alternativa E
Sabemos que o desvio-padrão é de 90kg/talhão e que 1 talhão tem 30.000 m², portanto:
\(\frac{90\ kg}{30.000\ m^2}=\frac{30\ kg}{10.000\ m^2}\)
Como 10.000 m² é um hectare, e 1 saca possui 60 kg, então 30kg é 0,5 saca, logo o desvio-padrão será:
\(0,5\ (saca/hectare)\)
Como o desvio-padrão é a raiz quadrada da variância:
\(0,5\ (saca/hectare)^2=0,25\ (saca/hectare)^2\)
Resposta Questão 10
Alternativa B
Para calcular o desvio-padrão, primeiramente calcularemos a média:
\(\bar{x}=\frac{48+54+50+46+44+52+49}7=\frac{343}7=49\)
Agora, calcularemos o quadrado da diferença entre os valores encontrados e a média:
(48 – 49)² = 1
(54 – 49)² = 25
(50 – 49)² = 1
(46 – 49)² = 9
(44 – 49)² = 25
(52 – 49)² = 9
(49 – 49)² = 0
Calculando a média entre esses valores:
\(σ^2=\frac{1+25+1+9+25+9+0}7\)
\(σ^2=\frac{70}7\)
\(σ^2=10\)
Por fim, calcularemos a raiz quadrada de 10:
\(σ=\sqrt{10}\)
Sabemos que \(\sqrt{10}\) está entre \(\sqrt{9}=3\) e \(\sqrt{16}=4\).
Então, a classificação é baixa.
Resposta Questão 11
Alternativa B
Note que eles possuem a mesma média, então olharemos para o desvio-padrão. O candidato que possui menor desvio-padrão é o mais regular; no caso, Marco.
Resposta Questão 12
Alternativa B
Sabemos que o desvio-padrão é a raiz quadrada da variância. Sendo assim, temos que:
\(σ_x=\sqrt{0,81}=0,9\)
\(σ_y=\sqrt{0,64}=0,8\)



