Questão 1
Questão 1 – (UFF) Segundo o matemático Leopold Kronecker (1823-1891), “Deus fez os números inteiros, o resto é trabalho do homem.” Os conjuntos numéricos são, como afirma o matemático, uma das grandes invenções humanas. Assim, em relação aos elementos desses conjuntos, é correto afirmar que:
A) o produto de dois números irracionais é sempre um número irracional.
B) a soma de dois números irracionais é sempre um número irracional.
C) entre os números reais 3 e 4 existe apenas um número irracional.
D) entre dois números racionais distintos existe pelo menos um número racional.
E) a diferença entre dois números inteiros negativos é sempre um número inteiro negativo.
Questão 2
Analise as afirmativas sobre os conjuntos numéricos a seguir.
I – Todo número negativo é um número inteiro.
II – Todo número natural é um número real.
III – Um número real pode ser racional ou irracional.
Julgue as afirmativas e encontre a alternativa correta.
A) Somente a I é falsa.
B) Somente a II é falsa.
C) Somente a III é falsa.
D) Somente a II é verdadeira.
E) Somente a III é verdadeira.
Questão 3
Ao realizar uma operação com os números reais, durante a resolução, Tiago encontrou uma divisão entre – 2,5 e 0,5. Sobre o resultado dessa divisão, podemos afirmar que:
A) o resultado é um número natural.
B) o resultado é um número racional, mas não é um número inteiro.
C) o resultado é um número racional e é um número inteiro.
D) o resultado é um número irracional.
E) o resultado é um número real, mas não é um número racional.
Questão 4
(IFG 2019) Os babilônicos talvez tenham usado a fórmula abaixo para obter aproximações interessantes de raízes quadradas de números não quadrados perfeitos.
![]()
Atribuindo a = 4/3 e b = 2/9 nessa fórmula, é correto afirmar que obtemos a aproximação:
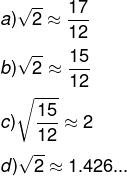
Questão 5
(UEL) Observe os seguintes números:
I. 2,212121...
II. 3,212223...
III. π/5
IV. 3,1416
V. √- 4
Assinale a alternativa que identifica os números irracionais.
A) I e II.
B) I e IV.
C) II e III.
D) II e V.
E) III e V.
Questão 6
A fração que representa a dízima periódica 2,727272…. é ?
A) 270/999
B) 30/11
C) 80/33
D) 272/99
E) 133/33
Questão 7
Se x = 0,535353… e y = 0,20202020…, a alternativa que representa o resultado de x – y é:
A) 11/99
B) 10/9
C) 11/33
D) 33/90
E) 73/99
Questão 8
Conhecendo dois números pertencentes ao conjunto dos números reais, julgue as afirmativas a seguir.
I – Na multiplicação de dois números reais, a ordem dos fatores não altera o produto.
II – Existe um elemento neutro na adição e na multiplicação de números reais. Esse elemento é o zero para ambas.
III – Todo número real possui um inverso.
Marque a alternativa correta.
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas II e III são verdadeiras.
E) Somente as afirmativas I e III são verdadeiras.
Questão 9
Durante a aula de Matemática, a professora pediu aos estudantes que eles listassem números racionais que estejam necessariamente entre os números 8 e 10. Os números escolhidos pelos estudantes foram:

Todos eles acertaram, exceto:
A) Amanda.
B) Bruna.
C) Camila.
D) Daniel.
E) Everaldo.
Questão 10
(Fuvest) Dividir um número por 0,0125 equivale a multiplicá-lo por:
A) 1/125.
B) 1/8.
C) 8.
D) 12,5.
E) 80.
Questão 11
Os conjuntos numéricos surgiram para atender as necessidades do homem, e a cada etapa foram se desenvolvendo novos conjuntos numéricos. Uma relação importante é a de inclusão. Dizemos que o conjunto A está contido em B quando todos os elementos do conjunto A estão contidos no conjunto B. Sobre os conjuntos numéricos, podemos afirmar que:
A) o conjunto dos números irracionais está contido no conjunto dos números racionais.
B) o conjunto dos números reais está contido no conjunto dos números racionais.
C) o conjunto dos números naturais está contido no conjunto dos números irracionais.
D) o conjunto dos números inteiros está contido tanto no conjunto dos números racionais quanto no conjunto dos números reais.
Questão 12
Sobre o resultado da expressão a seguir, podemos afirmar que:
![]()
A) o resultado é um número natural.
B) o resultado é um número inteiro não natural.
C) o resultado é um número racional não inteiro.
D) o resultado é um número real não racional.
Resposta Questão 1
Alternativa D.
A) Falsa, pois o produto de dois números irracionais pode gerar como resultado um número real. Por exemplo, o produto de √2 com ele mesmo, ou seja, √2×√2 = 2, é um número natural.
B) Falsa, pois a soma de um número com o seu simétrico, por exemplo, resulta em zero:
- √3 +√3 = 0.
C) Falsa, pois, entre dois números reais, existem infinitos números irracionais. Por exemplo, entre 3 e 4, existe o número irracional π e o √10.
D) Verdadeira.
E) Falsa, pois nem sempre isso ocorre. Por exemplo, -5 - (-6) = -5 + 6 = 1.
Resposta Questão 2
Alternativa A.
• I → Falsa, pois números decimais exatos negativos são racionais, mas não são inteiros. -7,5 é um exemplo de número negativo que não é inteiro.
• II → Verdadeira, pois o conjunto dos números naturais está contido no conjunto dos números reais.
• III → Verdadeira, pois o conjunto dos números reais é a união dos racionais com os irracionais.
Resposta Questão 3
Alternativa C.
Primeiro calcularemos a divisão:
- 2,5 : 0,5 = - 5
Analisando as alternativas, sabemos que -5 é um número racional e também é um número inteiro.
Resposta Questão 5
Dos números acima, são irracionais II e III, pois são números que não podem ser representados como uma fração.
Resposta Questão 6
Alternativa B.
Transformando a dízima em fração, é possível perceber que ela é uma dízima periódica simples. Quando isso ocorre, analisamos primeiro o período, que indica a quantidade de “9” que teremos no denominador. Note que há dois algarismos no período “72”, então, pelo método prático, sabemos que o denominador será 99. Já o numerador é 272 – 2 = 270. Sendo assim, a fração que geratriz da dízima será:
![]()
Resposta Questão 7
Alternativa C.
x – y = 0,535353… - 0,202020…
Realizando a operação, encontraremos a dízima 0,33333….
Agora, fazendo as divisões, encontraremos 11/33 = 0,3333... como a única alternativa que representa x – y.
Resposta Questão 8
Alternativa A.
• I → verdadeira, pois a multiplicação é comutativa, ou seja, a ordem das parcelas não altera o produto.
• II → falsa, pois o elemento neutro da multiplicação é o 1.
• III → falsa, 0 não possui inverso.
Resposta Questão 9
Alternativa B.
Dos números listados, todos são racionais, exceto a raiz não exata descrita por Bruna.
Resposta Questão 10
Alternativa B.
Vamos reescrever o número como uma fração irredutível:
![]()
Resposta Questão 11
Alternativa D.
Pela ordem dos conjuntos, sabemos que os naturais estão contidos nos inteiros, que estão contidos nos racionais, que estão contidos nos reais. Analisando cada uma das alternativas, a única que é verdadeira é a D.
Resposta Questão 12
Alternativa D.
Resolvendo a expressão, temos que:
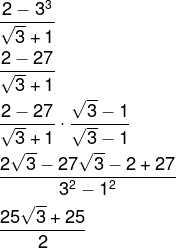
Como √3 é um número irracional, então toda a expressão é um número irracional. Analisando as alternativas, podemos afirmar que essa expressão resulta em um número real, mas que não é racional, já que o número real não racional é um número irracional.