Questão 1
Um sólido geométrico foi planificado, gerando a figura a seguir:
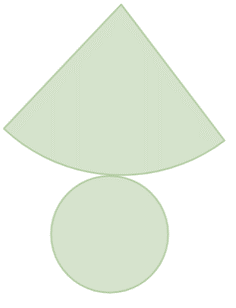
Analisando a imagem, podemos afirmar que o sólido geométrico que possui essa planificação é o/a:
A) cilindro.
B) esfera.
C) pirâmide.
D) cone.
E) círculo.
Questão 2
Um recipiente possui formato de cone, com raio igual a 8 cm e altura igual a 9 cm. Nessas condições, o volume desse recipiente, em cm³, é de:
A) 102 π
B) 156 π
C) 192 π
D) 200 π
E) 221 π
Questão 3
A área total de um cone que possui geratriz medindo 15 cm e raio igual a 12 cm é de:
(Use π = 3.)
A) 644 cm²
B) 696 cm²
C) 720 cm²
D) 818 cm²
E) 927 cm²
Questão 4
Buscando inovar nas embalagens de perfume e aumentar os ganhos, uma marca decidiu alterar as suas embalagens cilíndricas por embalagens no formato de cone, com a mesma altura e o mesmo raio da embalagem anterior. Podemos afirmar que o novo volume do perfume é:
A) a metade do volume anterior.
B) o dobro do volume anterior.
C) a terça parte do volume anterior.
D) o triplo do volume anterior.
E) igual ao volume anterior.
Questão 5
Analise o cone reto a seguir:
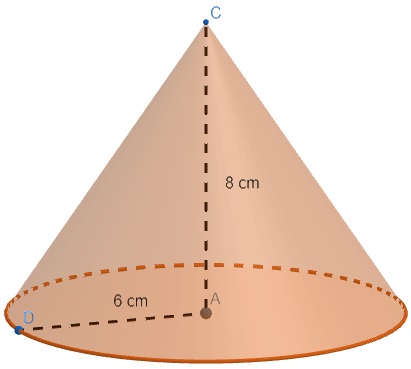
Podemos afirmar que a geratriz desse cone mede, em centímetros,
A) 9 cm.
B) 10 cm.
C) 11 cm.
D) 12 cm.
E) 15 cm.
Questão 6
Sobre o cone, julgue as afirmativas as seguir:
I. O cone é um corpo redondo.
II. O cone é uma pirâmide de base circular.
III. O cone é um sólido geométrico, mas não é um poliedro.
Marque a alternativa correta:
A) Somente I é falsa.
B) Somente II é falsa.
C) Somente III é falsa.
D) Todas são verdadeiras.
Questão 7
(Enem) Um arquiteto está fazendo um projeto de iluminação de ambiente e necessita saber a altura em que deverá instalar a luminária ilustrada na figura.
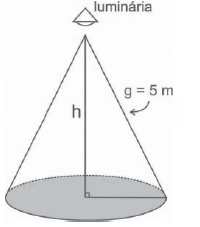
Sabendo que a luminária deverá iluminar uma área circular de 28,26 m², considerando π ≅ 3,14, a altura h será igual a
A) 3 m.
B) 4 m.
C) 5 m.
D) 9 m.
E) 16 m.
Questão 8
Um reservatório será confeccionado com o formato de cone reto, com diâmetro da base igual a 6 metros e altura igual a 4 metros. Sabendo que ele será feito todo em metal, qual é a quantidade de metal necessária para construir esse reservatório, em m²?
A) 20 π
B) 24 π
C) 29 π
D) 32 π
E) 35 π
Questão 9
A respeito do cone, julgue as afirmativas a seguir:
I. O cone é um sólido geométrico.
II. Podemos classificar o cone como um poliedro.
III. O cone possui uma base circular.
Marque a alternativa correta:
A) Somente I é falsa.
B) Somente II é falsa.
C) Somente III é falsa.
D) Todas são verdadeiras.
Questão 10
Um reservatório será confeccionado no formato de cone, utilizando 45 m² de um determinado material. Sabendo que o raio desse reservatório é de 2,5 metros, utilizando π = 3, podemos afirmar que a medida da geratriz desse cone é de:
A) 2,0 metros
B) 2,5 metros
C) 3,0 metros
D) 3,5 metros
E) 4,0 metros
Questão 11
(Cesgranrio) Um tanque cônico, de eixo vertical e vértice para baixo, tem água até a metade de sua altura. Se a capacidade do tanque é de 1200 l, então a quantidade de água nele existente é de:
A) 600 l
B) 450 l
C) 300 l
D) 200 l
E) 150 l
Questão 12
(Cefet-SC) Considere um copo em forma de cilindro e outro de forma cônica de mesma base e altura. Se eu encher completamente o copo cônico com água e derramar toda essa água no copo cilíndrico, quantas vezes terei que fazê-lo para encher completamente esse copo?
A) Apenas uma vez.
B) Duas vezes.
C) Três vezes.
D) Uma vez e meia.
E) É impossível saber, pois não se sabe o volume de cada sólido.
Resposta Questão 1
Alternativa D
A planificação do sólido geométrico observada é a de um cone. Note que há uma base circular e a área lateral do cone.
Resposta Questão 2
Alternativa C
Calculando o volume do cone, temos que:
\(V=\frac{\pi r^2\cdot h}{3}\)
\(V=\frac{\pi\cdot8^2\cdot9}{3}\)
\(V=\frac{\pi\cdot64\cdot9}{3}\)
\(V=\pi\cdot64\cdot3\)
\(V=192\ \pi\)
Resposta Questão 3
Alternativa E
Para calcular a área do cone, utilizamos a fórmula:
A = π · r (r + g)
Então, temos que:
A = 3 · 12 (12 + 15)
A = 36 · 27
A = 972 cm²
Resposta Questão 4
Alternativa C
Comparando o volume do cone com o volume do cilindro, ambos com a mesma altura e o mesmo raio, descobrimos que o volume do cone é \(\frac{1}{3}\) do volume do cilindro. Sendo assim, o novo volume é a terça parte do volume anterior.
Resposta Questão 5
Alternativa B
Pela relação pitagórica, temos que:
\(g^2=6^2+8^2\)
\(g^2=36+64\)
\(g^2=100\)
\(g=\sqrt{100}\)
\(g=10\ cm\)
Resposta Questão 6
Alternativa B
I. Verdadeira
O cone, de fato, é um corpo redondo. Os sólidos geométricos que se caracterizam assim possuem superfícies curvas.
II. Falsa
O cone não é um caso particular de pirâmide. Ele possui base circular, e as pirâmides possuem bases formadas por polígonos.
III. Verdadeira
Poliedros são figuras geométricas tridimensionais formadas por faces, vértices e arestas.
Resposta Questão 7
Alternativa B
Sabemos que a área da base é 28,26 m², então temos que:
\(\pi r^2=28,26\)
\(3,14r^2=28,26\)
\(r^2=\frac{28,26}{3,14}\)
\(r^2=9\)
\(r=\sqrt9\)
\(r=3\)
Conhecendo a geratriz g = 5, temos que:
\(g^2=r^2+h^2\)
\(5^2=3^2+h^2\)
\(25=9+h^2\)
\(25\ –9=h^2\)
\(h^2=16\)
\(h=\sqrt{16}\)
\(h=4\)
Resposta Questão 8
Alternativa B
Primeiramente, é necessário encontrar a medida da geratriz. Para isso, utilizaremos h = 4. O raio é a metade do diâmetro, logo r = 3, então:
\(g^2=3^2+4^2\)
\(g^2=9+16\)
\(g^2=25\)
\(g=\sqrt{25}\)
\(g=5\)
Sabendo o valor da geratriz, temos que:
A = π · r (r + g)
A = π · 3 (3 + 5)
\(A=3\pi\cdot8\)
\(A=24\ \pi\)
Resposta Questão 9
Alternativa B
I. Verdadeira
O cone é um sólido geométrico, pois sólidos geométricos são objetos tridimensionais definidos no espaço
II. Falsa
O cone não é um poliedro, pois ele não possui faces poligonais. Por causa de sua forma arredondada, ele é conhecido como um corpo redondo ou um sólido de revolução.
III. Verdadeira
Um sólido geométrico é considerado um cone quando ele possui base circular e é constituído pela rotação de um triângulo.
Resposta Questão 10
Alternativa D
Sabemos que:
\(A=\pi·r (r+g)\)
\(45=3·2,5 (2,5+g)\)
\(45=7,5\left(2,5+g\right)\)
\(\frac{45}{7,5}=2,5+g\)
\(6=2,5+g\)
\(6-2,5=g\)
\(3,5=g\)
Resposta Questão 11
Alternativa E
Sabemos que:
\(V=\frac{\pi r^2\cdot h}{3}\)
\(1200=\frac{\pi r^2\cdot h}{3}\)
\(1200\cdot3=\pi r^2h\)
\(\pi r^2h=3600\)
O volume ocupa metade do cone, logo temos \( \frac{r}{2}\) e \( \frac{h}{2}\). Sendo assim:
\(V_2=\frac{\pi\left(\frac{r}{2}\right)^2\cdot\frac{h}{2}}{3}\)
\(V_2=\frac{\pi\cdot\frac{r^2}{4}\cdot\frac{h}{2}}{3}\)
\(V_2=\frac{\frac{\pi r^2h}{8}}{3}\)
\(V_2=\frac{\frac{3600}{8}}{3}\)
\(V_2=\frac{450}{3}\)
\(V_2=150\)
O volume, portanto, é de 150 l.
Resposta Questão 12
Alternativa C
O volume de um cilindro que possui a mesma base e altura de um cone é sempre igual ao triplo do volume do cone, ou seja, o volume do cone é um terço do volume do cilindro. Sendo assim, é necessário usar o cone três vezes para encher um cilindro.



