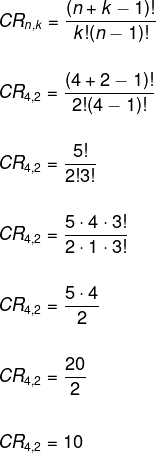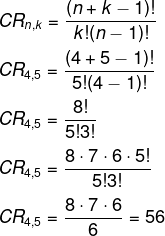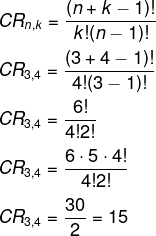Questão 1
Em uma sorveteria são oferecidos 4 sabores de milkshake, sendo eles chocolate, morango, amendoim e baunilha. Com esses sabores, de quantas maneiras distintas um cliente pode fazer o pedido de dois milkshakes?
A) 20
B) 15
C) 10
D) 8
E) 5
Questão 2
(Enem 2017) Um brinquedo infantil caminhão-cegonha é formado por uma carreta e dez carrinhos nela transportados, conforme a figura.
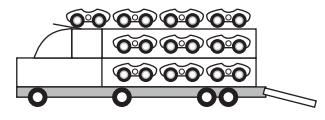
No setor de produção da empresa que fabrica esse brinquedo, é feita a pintura de todos os carrinhos para que o aspecto do brinquedo fique mais atraente. São utilizadas as cores amarelo, branco, laranja e verde, e cada carrinho é pintado apenas com uma cor. O caminhão-cegonha tem uma cor fixa. A empresa determinou que em todo caminhão-cegonha deve haver pelo menos um carrinho de cada uma das quatro cores disponíveis. Mudança de posição dos carrinhos no caminhão-cegonha não gera um novo modelo do brinquedo.
Com base nessas informações, quantos são os modelos distintos do brinquedo caminhão-cegonha que essa empresa poderá produzir?
A) C6,4
B) C9,3
C) C10,4
D) 64
E) 46
Questão 3
Matheus foi até uma loja de calçados para comprar meias. Na loja, ele percebeu que havia 8 modelos distintos. Sabendo que ele deseja comprar 6 pares de meia, de quantas maneiras diferentes ele pode realizar essa compra?
A) 180
B) 360
C) 540
D) 720
E) 1080
Questão 4
No dia da árvore, a escola de Heitor resolveu incentivar a plantação de mudas nas casas de seus alunos. Havia 3 opções de mudas: ipê, cajá-manga e aroeira. Sabendo que cada estudante podia escolher 4 mudas para levar para casa, o número de maneiras distintas que Heitor poderia fazer essa escolha seria:
A) 36
B) 30
C) 25
D) 20
E) 15
Questão 5
Durante um festival de massas realizado na cidade de Nova Veneza, no estado de Goiás, dona Ana apresentou a seus clientes 5 novos sabores de molhos para serem colocados no macarrão. Se um cliente decidir pedir 3 porções de macarrão, de quantas maneiras distintas ele pode escolher os molhos para essas 3 porções?
A) 35
B) 42
C) 50
D) 62
E) 70
Questão 6
Natália tem se dedicado durante vários dias para conseguir uma boa nota no concurso do qual ela pretende participar. Todos os dias, ela estuda durante 3 horas seguidas e a cada hora ela escolhe se vai mudar de disciplina ou não. Existem dias em que ela decide estudar somente uma disciplina durante as 3 horas, dias em que ela decide estudar uma disciplina diferente em cada hora e dias em que ela decide se dedicar durante 2 horas para uma disciplina e estudar outra na terceira hora. Sabendo que no edital estão previstas questões sobre conhecimentos específicos, legislação, língua portuguesa e matemática, o número de maneiras distintas as quais Natália pode organizar sua rotina de estudo é igual a:
A) 12
B) 20
C) 32
D) 42
E) 50
Questão 7
Para movimentar as redes sociais de sua empresa de docinhos, Ana Júlia decidiu fazer publicidade por meio de sorteios. Serão realizados, ao todo, 3 sorteios. Em cada um deles, o ganhador receberá um kit de festa com 50 docinhos diversos. Sabendo que todos os seus seguidores poderão participar de todos os sorteios, o número de maneiras distintas que ela pode obter como resultado dos três sorteios pode ser calculado por:
A) uma permutação simples.
B) uma combinação simples.
C) um arranjo simples.
D) um arranjo com repetições.
E) uma combinação com repetição.
Questão 8
Na casa de Jéssica, durante o preparo do almoço, o gás acabou. Como já estava tarde, ela decidiu fazer o pedido de marmitas, uma para ela e uma para cada um de seus 4 irmãos. Ao realizar a ligação para o restaurante, foram oferecidos para ela 4 tipos diferentes de carne (peixe, porco, boi e frango). De quantas maneiras distintas Jéssica pode realizar esse pedido?
A) 32
B) 40
C) 56
D) 92
E) 180
Questão 9
O bingo é uma prática muito comum nas festas de final de ano na família de Laís. Este ano, sua tia Griselda levou 2 blusas idênticas para serem prendas do bingo. Sabendo que independentemente de ganhar ou perder, todos os 6 membros da família participarão de todos os sorteios, o número de maneiras distintas que essas 2 blusas podem ser sorteadas é:
A) 42
B) 38
C) 32
D) 25
E) 21
Questão 10
Em uma lanchonete, há três sabores diferentes de suco. De quantas maneiras distintas um cliente pode fazer o pedido de 4 sucos?
A) 12
B) 15
C) 21
D) 28
E) 30
Questão 11
Sobre a combinação com repetição, julgue as afirmativas a seguir:
I → Na combinação com repetição, conjuntos com elementos iguais em ordem diferente geram agrupamentos diferentes.
II → Na combinação com repetição, um mesmo elemento do conjunto pode aparecer mais de uma vez.
III → A escolha de senhas é um exemplo de combinação com repetição.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) As afirmativas II e III são verdadeiras.
E) Todas as afirmativas são verdadeiras.
Questão 12
Considere os todos os agrupamentos a seguir, feitos com as letras A, B e C:
{A, B, C}, {A, A, B} {A, A, C}, {A, A, A}, {A, B, B}, {B, B, C}, {B, B, B}, {A, C, C}, {B, C, C} e {C, C, C}
Analisando esses agrupamentos, podemos classificá-los como:
A) uma combinação simples.
B) uma permutação simples.
C) um arranjo simples.
D) um arranjo completo.
E) uma combinação completa.
Resposta Questão 1
Resposta Questão 2
Alternativa B.
Note que temos uma combinação com repetição, com 4 opções de cores para 6 carrinhos, ou seja, n = 4 e k = 6. Analisando as alternativas, transformaremos a combinação com repetição em uma combinação simples:
CRn,k = Cn+k – 1, k
CR4,6 = C4+6 – 1, 6
CR4,6 = C9,6
Note que não há uma alternativa com essa combinação simples, mas sabemos que C9,6 = C9,3.
Resposta Questão 3
Alternativa D
Calculando a combinação com repetição de 8 elementos tomados de 6 em 6, temos que:
\(CR_{n,k}=\frac{\left(n+k-1\right)!}{k!\left(n-1\right)!}\)
\(CR_{8,6}=\frac{\left(8+6-1\right)!}{6!\left(8-1\right)!}\)
\(CR_{8,6}=\frac{13!}{6!7!}\)
\(CR_{8,6}=\frac{13\cdot12\cdot11\cdot10\cdot9\cdot8\cdot7!}{6!7!}\)
\(CR_{8,6}=\frac{1235520}{6!}=1716\)
Resposta Questão 4
Alternativa E
Calculando a combinação com repetição, temos n = 3 e k = 4.
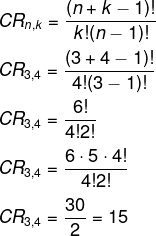
Resposta Questão 5
Alternativa A
Queremos a combinação com repetição de 5 elementos tomados de 3 em 3:
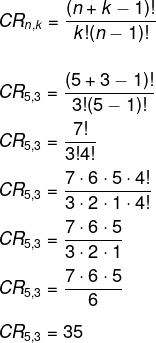
Resposta Questão 6
Alternativa B
Analisando a questão, vamos querer uma combinação com repetição de 5 disciplinas tomadas de 3 em 3.
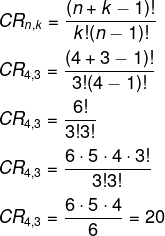
Resposta Questão 7
Alternativa E
Note que a ordem não é importante, e que um mesmo elemento pode estar no agrupamento mais de uma vez, então essa é uma combinação com repetição.
Resposta Questão 9
Alternativa E
Queremos calcular a combinação com repetição de 6 elementos tomados de 2 em 2.
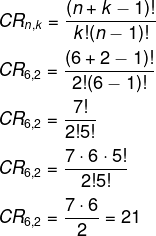
Resposta Questão 11
Alternativa B
I → Falsa
Na combinação, a mudança da ordem dos elementos não gera um novo agrupamento.
II → Verdadeira
Como o nome sugere, na combinação com repetição, pode haver um ou mais termos que se repetem.
III → Falsa
Em senhas, a ordem é importante. Logo, se tratam de arranjos com repetição, e não combinações com repetição.
Resposta Questão 12
Alternativa E
Note que nesses agrupamentos a ordem não é importante. Além disso, há repetição de um mesmo elemento. Portanto, estamos diante de uma combinação completa de três elementos tomados de 3 em 3.