Questão 1
(Vunesp) Para uma prova, 150 candidatos deveriam ser acomodados nas salas A, B, C e D de um colégio, com capacidade para receber 60, 50, 40 e 30 candidatos, respectivamente. A organização decidiu preencher inicialmente todos os lugares da sala menor, e os candidatos restantes foram repartidos entre as demais salas de forma diretamente proporcional à capacidade de cada uma. O número de lugares não ocupados na sala de maior capacidade foi igual a:
A) 8
B) 10
C) 12
D) 14
E) 16
Questão 2
(Enem 2012) Nos shopping centers, costumam existir parques com vários brinquedos e jogos. Os usuários colocam créditos em um cartão, que são descontados por período de uso dos jogos.
Dependendo da pontuação da criança no jogo, ela recebe certo número de tíquetes para trocar por produtos nas lojas dos parques.
Suponha que o período de uso de um brinquedo em certo shopping custa R$ 3 e que uma bicicleta custa 9200 tíquetes.
Para uma criança que recebe 20 tíquetes por tempo de jogo, o valor, em reais, gasto com créditos para obter a quantidade de tíquetes para trocar pela bicicleta é
A) 153.
B) 460.
C) 1218.
D) 1380.
E) 3066.
Questão 3
(Enem)
Fontes alternativas
Há um novo impulso para produzir combustível a partir de gordura animal. Em abril, a High Plains Bioenergy inaugurou uma biorrefinaria próxima a uma fábrica de processamento de carne suína em Guymon, Oklahoma. A refinaria converte a gordura do porco, juntamente com o óleo vegetal, em biodiesel. A expectativa da fábrica é transformar 14 milhões de quilogramas de banha em 112 milhões de litros de biodiesel.
Revista Scientific American. Brasil, ago. 2009 (adaptado).
Considere que haja uma proporção direta entre a massa de banha transformada e o volume de biodiesel produzido.
Para produzir 48 milhões de litros de biodiesel, a massa de banha necessária, em quilogramas, será de, aproximadamente,
A) 6 milhões.
B) 33 milhões.
C) 78 milhões.
D) 146 milhões.
E) 384 milhões.
Questão 4
(Enem) A suspeita de que haveria uma relação causal entre tabagismo e câncer de pulmão foi levantada pela primeira vez a partir de observações clínicas. Para testar essa possível associação, foram conduzidos inúmeros estudos epidemiológicos.
Dentre esses, houve o estudo do número de casos de câncer em relação ao número de cigarros consumidos por dia, cujos resultados são mostrados no gráfico a seguir.
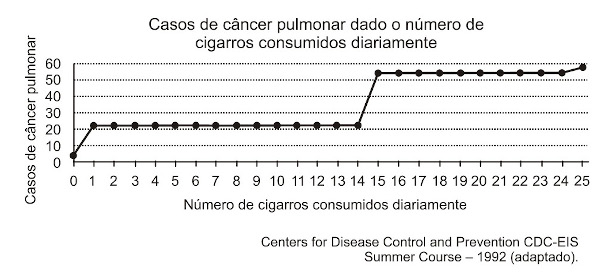
De acordo com as informações do gráfico,
A) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas inversamente proporcionais.
B) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas que não se relacionam.
C) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas diretamente proporcionais.
D) uma pessoa não fumante certamente nunca será diagnosticada com câncer de pulmão.
E) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas que estão relacionadas, mas sem proporcionalidade.
Questão 5
Os ângulos de um triângulo são diretamente proporcionais aos números 3, 7 e 15, então, podemos afirmar que o menor ângulo mede:
A) 108º
B) 50,4º
C) 21,6º
D) 42º
E) 50,4º
Questão 6
Os lados de um retângulo são proporcionais a 2 e 3. Sabendo que a sua área é de 216 m², as dimensões dos retângulos são, respectivamente:
A) 12 e 18
B) 4 e 54
C) 8 e 27
D) 10 e 26
E) 13,5 e 16
Questão 7
Uma herança de R$ 1.500.000 foi dividida entre os filhos de forma diretamente proporcional à idade de cada um deles. Sabendo que há três filhos, com 14, 16 e 20 anos de idade, podemos afirmar que o filho do meio receberá:
A) R$ 600.000
B) R$ 420.000
C) R$ 480.000
D) R$ 500.000
E) R$ 450.000
Questão 8
Os ângulos de um quadrilátero são proporcionais a 3, 6, 12, 15. Assim, podemos afirmar que o valor do maior ângulo é:
A) 150º
B) 120º
C) 60º
D) 30º
E) 135º
Questão 9
A idade de três irmãos é diretamente proporcional a 4, 6 e 10 anos. Sabendo que a soma da idade dos três é igual a 70, podemos afirmar que o mais novo possui:
A) 10 anos
B) 12 anos
C) 14 anos
D) 16 anos
E) 18 anos
Questão 10
Um automóvel faz 35 km com 5 litros de etanol. Realizando uma viagem de uma cidade para outra, com base nesse consumo, qual deve ser a quantidade de etanol necessária para percorrer 196 km?
A) 28 litros
B) 25 litros
C) 20 litros
D) 30 litros
E) 18 litros
Questão 11
Das relações entre as grandezas a seguir, identifique aquela que não é diretamente proporcional.
A) Quantidade de funcionários e produtividade
B) Distância percorrida e consumo do veículo
C) Velocidade do automóvel e tempo para completar o percurso
D) Valor pago pela verdura e peso
Questão 12
Um triângulo retângulo possui os lados diretamente proporcionais a 3, 4 e 5. Sabendo que sua hipotenusa é igual a 31 cm, o valor do perímetro desse triângulo é:
A) 28,4 cm
B) 42,6 cm
C) 65 cm
D) 74,4 cm
E) 82,8 cm
Resposta Questão 1
Alternativa C
Sabendo que a sala menor será toda preenchida, 150 – 30 = 120 candidatos restantes. Os 120 candidatos restantes serão divididos de forma proporcional, então, sabemos que:
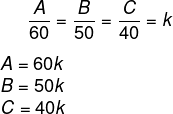
Sabemos que:
A + B + C = 120
Substituindo os valores encontrados, temos que:
60k + 50k + 40k = 120
150k = 120
k = 120/150
k = 0,8
Dessa forma, a ocupação de cada uma das salas será:
60k → 60 · 0,8 = 48
Como há uma capacidade de 60 lugares, 60 – 48 = 12 lugares não ocupados.
Resposta Questão 2
Alternativa D
Sabendo que a criança precisa de 9200 tíquetes, e que ela ganha 20 por período, ao realizar a divisão, encontraremos quantos períodos ela jogará.
9200 : 20 = 460
Para cada período, gasta-se R$ 3. Sendo assim, 460 · 3 = 1380.
Resposta Questão 3
Alternativa A
Sabendo que 14 milhões de quilogramas de banha são convertidos em 112 milhões de litros de biodiesel, ao dividir 112 milhões por 14, vamos encontrar quantos litros de biodiesel podem ser produzidos com 1 milhão de quilogramas de banha.
112 : 14 = 8, ou seja, 1 milhão de kg de banha é convertido em 8 milhões de litros de biodiesel. Agora, para saber quantos kg de banha são necessários para produzir 48 milhões de litros de biodiesel, basta dividir 48 por 8.
48 : 8 = 6 milhões
Resposta Questão 4
Alternativa E
Sabe-se que existe sim relação entre o tabagismo e os casos de câncer de pulmão, porém, analisando o gráfico, é possível perceber que o crescimento não é proporcional, note que, em alguns intervalos, os casos de câncer são constantes.
Resposta Questão 5
Alternativa C
Sabemos que a soma dos ângulos internos de um triângulo é sempre 180º.
Seja x, y, e z os ângulos do triângulo, como eles são proporcionais a 3,7 e 15, então, temos que:
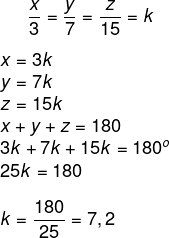
x = 3 · 7,2 = 21,6º
y = 7 · 7,2 = 50,4º
z = 15 · 7,2 = 108º
Resposta Questão 6
Alternativa A
Sabendo que os lados são proporcionais a 2 e 3, então, seja x e y os lados do retângulo, existe k, tal que:
![]()
Assim, temos que:
x = 2k
y = 3k
Sabendo que a área é 216 m², então, temos que:
A = 2k · 3k = 6k²
6k² = 216
k² = 216/6
k² = 36
k = √36
k = 6
Resposta Questão 7
Alternativa C
Sejam A, B e C os filhos de 14, 16 e 20 anos, respectivamente:
![]()
x = 14k
y = 16k
z = 20k
Então, temos que:
14k + 16k + 20k = 1.500.000
50k = 1.5000.000
k = 1.500.000/50
k = 30.000
y = 16 · 30.000 = 480.000
Resposta Questão 8
Alternativa A
A soma dos ângulos internos de um quadrilátero é igual a 360º. Sejam x, y, z e w os ângulos do quadrilátero, temos que:
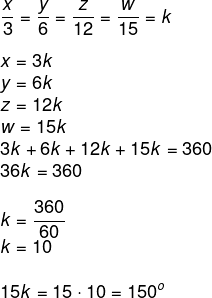
Resposta Questão 9
Alternativa C
Como as idades são proporcionais, e sejam A, B e C as idades de cada um desses irmãos, então, temos que:
![]()
Assim, temos que:
A = 4k
B = 6k
C = 10k
Sabendo que a soma é igual a 70, então:
4k + 6k + 10 k = 70
20k = 70
k = 70/20
k = 3,5
Como queremos a idade do mais novo:
A = 4 · 3,5 = 14 anos
Resposta Questão 10
Alternativa A
Sabendo que existe proporção entre a distância percorrida e o consumo de combustível, ao dividir 35 por 5, encontraremos o consumo 35 : 5 = 7 km/l. Sabendo que a viagem é de 196 km, 196 : 7 = 28 litros.
Resposta Questão 11
Resolução
Alternativa C. Quanto maior a velocidade, menor será o tempo gasto no percurso.
Resposta Questão 12
Alternativa D
Sejam a e b os catetos do triângulo, vamos montar a proporção:
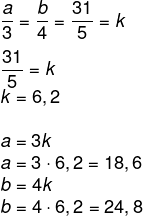
P = a + b + 31
P = 18,6 + 24,8 + 31 = 74,4



