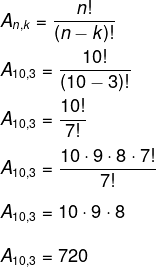Questão 1
Na competição de interclasse da escola, há 10 turmas competindo entre si pela medalha de ouro, prata e bronze. Então, o número de maneiras distintas que o pódio pode ser formado é igual a:
A) 120
B) 460
C) 540
D) 720
E) 90
Questão 2
Durante uma palestra no auditório, há 6 cadeiras vazias consecutivas, assim, o número de maneiras distintas que Amanda, Beatriz, Carla e Daiane podem se sentar nessas cadeiras é igual a:
A) 720
B) 360
C) 120
D) 90
E) 15
Questão 3
As senhas bancárias são construídas com 4 dígitos. Durante a criação da senha, a gerente da Karla recomendou que ela criasse uma senha com 4 dígitos, todos distintos entre si. Suponha que Karla seguiu a recomendação de sua gerente, assim, o número de senhas distintas que ela pode criar é igual a:
A) 210
B) 420
C) 1840
D) 2520
E) 5040
Questão 4
Em uma reunião do sindicato, com 15 membros, devem ser escolhidos o presidente e vice-presidente do sindicato. Sabendo que cada membro pode ser votado para qualquer um dos cargos, mas que ninguém poderia exercer as duas funções simultaneamente, então, o número de escolhas distintas para os dois cargos é igual a:
A) 420
B) 360
C) 210
D) 120
E) 42
Questão 5
Durante as aulas, um professor elaborou quatro questões distintas para que os alunos respondessem no quadro. A escolha dos alunos que responderão as questões será feita por forma de sorteio, sendo que um aluno sorteado responderá uma única questão. Então, de quantas formas possíveis esses alunos podem ser selecionados, sabendo que há 20 alunos na turma?
A) 4845
B) 19.380
C) 80.210
D) 116.280
E) 58.140
Questão 6
O setor de Recursos Humanos de uma determinada empresa vai realizar a contratação de 4 funcionários para os cargos de vendedor interno, atendente, auxiliar administrativo e vendedor externo. A seleção será realizada em duas etapas, a primeira será a análise de currículo de todos os candidatos, independentemente do cargo. Durante a análise de currículo, serão selecionados 10 candidatos para participar da entrevista. Durante a entrevista, o setor de Recursos Humanos terá que descartar 6 candidatos e escolher 4 já com cargos definidos de acordo com o perfil dos candidatos. Sendo assim, o número de agrupamentos possíveis para a contratação desses 4 funcionários será:
A) 1725
B) 2540
C) 3780
D) 5040
E) 10.080
Questão 7
Por motivos de segurança, Renato decidiu alterar a sua senha das redes sociais. Para que ele não se esqueça de suas senhas, ele sempre escolhe usar três letras do seu nome seguidas do dia e do mês de nascimento. Sabendo que a senha antiga era “ren0203”, o total de senhas possíveis que ele pode criar para essa nova senha é:
A) 120
B) 119
C) 118
D) 89
E) 19
Questão 8
Natália decidiu criar seu próprio idioma. Primeiro ela construiu um alfabeto formado pelos símbolos ∞, α, γ, Ω, γ, ɸ. Sabendo que as palavras desse idioma são compostas pela junção de, no mínimo, dois símbolos, então, o número de palavras distintas desse idioma que não possui símbolos repetidos é igual a:
A) 24
B) 720
C) 1480
D) 1950
E) 2370
Questão 9
(Consultec – adaptada) Após um assalto, várias testemunhas foram ouvidas, mas não houve consenso quanto à placa do automóvel usado pelo assaltante na sua fuga. Através das informações dessas testemunhas, concluiu-se que a placa do veículo era constituída de 3 vogais distintas e 4 algarismos também distintos, sendo que os 2 últimos algarismos eram os dígitos 0 e 1, nessa ordem.
Com base nesses dados, pode-se afirmar que o número de veículos a serem investigados é
A) 560
B) 1120
C) 3360
D) 6720
E) 8240
Questão 10
Durante os jogos internos de um colégio, foi organizado o campeonato de xadrez. Nele todos os inscritos se enfrentariam duas vezes, sendo que, na primeira partida, um inscrito começaria o jogo, e, na segunda partida, o outro começaria o jogo. O vencedor será o competidor que conseguir a maior pontuação durante o campeonato. Sabendo que 16 estudantes jogarão, e que 8 partidas sempre acontecem simultaneamente, com um tempo máximo de 50 minutos por rodada, então, o tempo gasto para realizar todas as partidas, ignorando os intervalos, é de:
A) 25 horas
B) 22 horas
C) 24 horas
D) 18 horas
E) 12 horas
Questão 11
Para incentivar a participação dos estudantes nas olimpíadas de matemática, a professora decidiu sortear brindes para os que comparecessem na prova. Havia três prêmios, o primeiro sorteado ganharia um dia no rodízio de pizza, o segundo receberia uma pizza grande em casa, e o terceiro ganharia uma caixa de bombom. Sabendo que 16 estudantes compareceram na prova, e que um aluno não poderia ganhar mais de um prêmio, então, o número de resultados possíveis para esses sorteios é igual a:
A) 430
B) 520
C) 975
D) 1850
E) 3360
Questão 12
(Enem) Doze times se inscreveram em um torneio de futebol amador. O jogo de abertura do torneio foi escolhido da seguinte forma: primeiro foram sorteados 4 times para compor o Grupo A. Em seguida, entre os times do Grupo A, foram sorteados 2 times para realizar o jogo de abertura do torneio, sendo que o primeiro deles jogaria em seu próprio campo, e o segundo seria o time visitante. A quantidade total de escolhas possíveis para o Grupo A e a quantidade total de escolhas dos times do jogo de abertura podem ser calculadas por meio de:
A) uma combinação e um arranjo, respectivamente.
B) um arranjo e uma combinação, respectivamente.
C) um arranjo e uma permutação, respectivamente.
D) duas combinações.
E) dois arranjos.
Resposta Questão 1
Resposta Questão 2
Alternativa B
Tendo 6 opções de cadeiras, escolheremos 4 delas. Note que a ordem é importante, então, calcularemos o arranjo de 6 elementos tomados de 4 em 4.
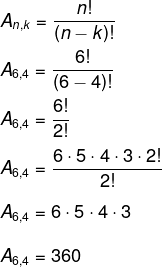
Resposta Questão 3
Alternativa E
Existem 10 opções possíveis de símbolos. Como em senhas a ordem é importante, e, nesse caso, ela possuí dígitos distintos, então, estamos calculando um arranjo de 10 elementos tomados de 4 em 4.
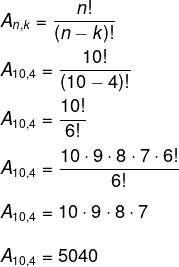
Resposta Questão 4
Alternativa C
Será feita a escolha de 2 entre os 15 membros do sindicato. Note que a ordem, nesse caso, é importante, então, estamos trabalhando com um arranjo de 15 elementos tomados de 2 em 2.
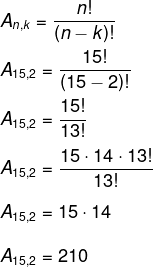
Resposta Questão 5
Alternativa D
Serão escolhidos 4 estudantes entre os 20. Note que a ordem é importante, então, calcularemos o arranjo de 20 elementos tomados de 4 em 4.
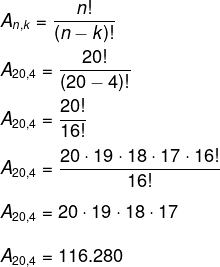
Resposta Questão 6
Alternativa D
Serão escolhidos entre os 10 candidatos 4 para serem funcionários, com cargos já definidos. Então, calcularemos o arranjo de 10 elementos tomados de 4 em 4.
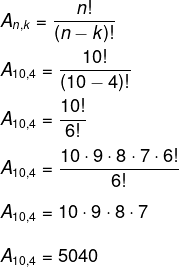
Resposta Questão 7
Alternativa B
A senha será formada com 3 letras do nome Renato, logo, será um arranjo de 6 elementos escolhidos de 3 em 3.
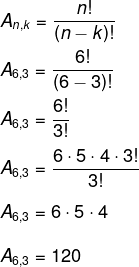
Como a sequência “ren” já foi utilizada, então, 120 – 1 = 119 senhas possíveis.
Resposta Questão 8
Alternativa D
Nesse nosso idioma, há 6 símbolos que compõem o alfabeto, então, queremos encontrar o valor da soma da quantidade de palavras que podemos formar com 2, 3, 4, 5 ou 6 símbolos. Como todos eles são distintos, logo, estamos calculando arranjos:
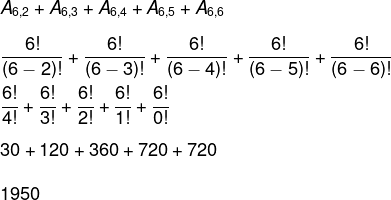
Resposta Questão 9
Alternativa C
Sabemos que as placas são feitas por 3 vogais seguidas de 4 algarismos, todos distintos. Primeiro escolheremos os algarismos. Existem 5 vogais no nosso alfabeto, então, trata-se de um arranjo de 5 elementos tomados de 3 em 3. Falta, ainda, escolhermos 2 números, diferentes de 0 e de 1, já que os algarismos também são distintos, ou seja, há 8 possibilidades, e vamos escolher de 2 em 2. Então, o total T de placas possíveis é dado pelo produto de A5,3 e A8,2
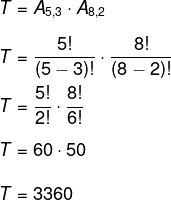
Resposta Questão 10
Alternativa A
Primeiro calcularemos quantas partidas ocorrerão calculando o arranjo de 16 elementos tomados de 2 em 2.
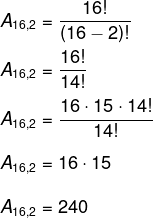
Serão realizadas 240 partidas. Como 10 partidas acontecem simultaneamente, então, teremos um total de 240 : 8 = 30 rodadas.
Se cada rodada dura, no máximo, 50 minutos, então, 30 · 50 = 1500 minutos.
Para transformar minutos em horas, basta dividir por 60, então, temos que 1500 : 60 = 25 horas.
Resposta Questão 11
Alternativa E
Vamos calcular um arranjo de 16 elementos tomados de 3 em 3.
\(A_{16,3}=\frac{16!}{\left(16-3\right)!}\)
\(A_{16,3}=\frac{16!}{13!}\)
\(A_{16,3}=\frac{16\cdot15\cdot14\cdot13!}{13!}\)
\(A_{16,3}=16\cdot15\cdot14\)
\(A_{16,3}=3360\)
Resposta Questão 12
Alternativa A
Para saber qual o tipo de agrupamento a que o problema está se referindo, basta analisar se a ordem é importante ou não.
No primeiro agrupamento, serão sorteados 4 times entre os 12 para compor o Grupo A. Note que a ordem em que um time é sorteado não é relevante, desde que ele esteja entre os 4 sorteados, então, trata-se de uma combinação.
Já na segunda escolha, dos 4 times serão sorteados 2, só que o primeiro sorteado jogará em casa, logo, a ordem é importante, o que faz com que esse agrupamento seja calculado por um arranjo.
Assim, temos, respectivamente, uma combinação e um arranjo.