Questão 1
Buscando reduzir a quantidade de furtos de bicicletas, uma cidade decidiu realizar o emplacamento das mesmas. A placa será composta por 2 letras e 3 números. Sendo assim, o número de bicicletas que podem ser emplacadas nessa cidade é de
A) 82
B) 780
C) 1560
D) 20.200
E) 67.600
Questão 2
Qual é a quantidade de números com 4 algarismos que podemos formar utilizando apenas os algarismos que são números ímpares?
A) 20
B) 80
C) 625
D) 1024
E) 2048
Questão 3
Para o cadastro da senha do cartão de crédito de um banco novo, o banco Mundo, os usuários escolhem 4 algarismos distintos ou não para fazerem a sua senha. Um novo usuário desse banco criará sua senha utilizando somente os algarismos presentes no dia e mês do seu nascimento, que é dia 02 de novembro. O número de senhas que esse usuário pode criar é:
A) 12
B) 20
C) 27
D) 81
E) 120
Questão 4
Em uma avenida, há 6 semáforos alinhados. Sabemos que a cor do semáforo se altera entre verde, vermelha e amarela. Se um fotógrafo resolver tirar fotos dessa avenida de maneira que os 6 semáforos sejam capturados, quantas são as sequências de cores que podem ser capturadas pela câmera?
A) 18
B) 216
C) 324
D) 729
E) 1152
Questão 5
A quantidade de agrupamentos ordenados que podemos formar com as letras {A , B, C, D} contendo 3 letras, podendo haver repetição, pode ser calculada por:
A) \(3\cdot4\ \)
B) \( 4^3\)
C) \(3^4\)
D) \(3!\)
E) \(4!\)
Questão 6
(Enem 2017) Uma empresa construirá sua página na internet e espera atrair um público de aproximadamente um milhão de clientes. Para acessar essa página, será necessária uma senha com formato a ser definido pela empresa. Existem cinco opções de formato oferecidas pelo programador, descritas no quadro, em que “L” e “D” representam, respectivamente, letra maiúscula e dígito.
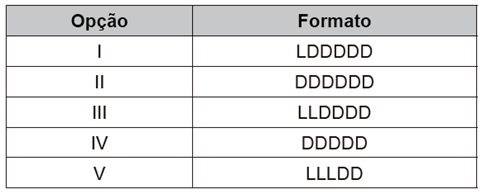
As letras do alfabeto, entre as 26 possíveis, bem como os dígitos, entre os 10 possíveis, podem se repetir em qualquer das opções. A empresa quer escolher uma opção de formato cujo número de senhas distintas possíveis seja superior ao número esperado de clientes, mas que esse número não seja superior ao dobro do número esperado de clientes.
A opção que mais se adequa às condições da empresa é:
A) I
B) II
C) III
D) IV
E) V
Questão 7
(Iades) Considere a tabela a seguir:
|
000 |
|
001 |
|
010 |
|
011 |
|
100 |
|
101 |
|
110 |
|
111 |
Com base na tabela apresentada, o que ocorre é um(a):
A) arranjo com repetição.
B) combinação complementar.
C) permutação simples.
D) permutação circular.
E) arranjo, com n = p.
Questão 8
(Enem 2005) A escrita Braille para cegos é um sistema de símbolos no qual cada caráter é um conjunto de 6 pontos dispostos em forma retangular, dos quais pelo menos um se destaca em relação aos demais.
Por exemplo, a letra A é representada por:

O número total de caracteres que podem ser representados no sistema Braille é:
A) 12
B) 31
C) 36
D) 63
E) 720
Questão 9
Em uma fase teste de um jogo, cada usuário recebe uma combinação de 3 símbolos entre os caracteres @, #, $, &, * para nomear o personagem. Sabendo que pode haver repetição entre os caracteres, mas que dois usuários não podem possuir o mesmo nome, o número de usuários N que podem ser criados nesse jogo durante a fase de teste é calculado por:
A) N = \(\frac{5!}{2!}\)
B) N = 5!
C) N = \( 5^3\)
D) N = \(\frac{5!}{2!3!}\)
E) N = 3!
Questão 10
Três amigos irão a uma loja especializada em coxinhas que possui 10 sabores diferentes. Se cada um deles comprará uma coxinha, o número de maneiras distintas que eles podem fazer o pedido é igual a
A) 30
B) 90
C) 270
D) 1000
E) 59049
Questão 11
Em uma empresa que realiza atendimento ao cliente, antes de encerrar o contato, o cliente classifica o atendimento entre os seguintes critérios: excelente, bom, regular, ruim ou muito ruim. Ao final da semana, o funcionário recebe o extrato dos seus atendimentos, contendo em ordem as notas recebidas por cada um dos contatos realizados durante a semana. Se em determinada semana foram atendidos 20 clientes, o número de sequências distintas que o atendente pode receber contendo as notas dos seus contatos pode ser calculado por:
A) 57
B) 520
C) 20 ⋅ 7
D) 20 ⋅ 5
E) 205
Questão 12
(Enem 2013) Um banco solicitou aos seus clientes a criação de uma senha pessoal de seis dígitos, formada somente por algarismos de 0 a 9, para acesso à conta corrente pela internet. Entretanto, um especialista em sistemas de segurança eletrônica recomendou à direção do banco recadastrar seus usuários, solicitando, para cada um deles, a criação de uma nova senha com seis dígitos, permitindo agora o uso das 26 letras do alfabeto, além dos algarismos de 0 a 9. Nesse novo sistema, cada letra maiúscula era considerada distinta de sua versão minúscula. Além disso, era proibido o uso de outros tipos de caracteres.
Uma forma de avaliar uma alteração no sistema de senhas é a verificação do coeficiente de melhora, que é a razão do novo número de possibilidades de senhas em relação ao antigo. O coeficiente de melhora da alteração recomendada é:
A) \(\frac{{62}^6}{{10}^6}\)
B) \(\frac{62!}{10!}\)
C) \(\frac{62!4!}{10!56!}\)
D) 62! – 10!
E) 626 – 106
Resposta Questão 1
Alternativa E
Como existem 26 letras em nosso alfabeto, 2 serão escolhidas e pode haver repetição, então calcularemos um arranjo com repetição. O mesmo ocorre com os números: existem 10 algarismos e escolheremos 3. Assim, temos que:
\(AR_{26,2}\cdot AR_{10,3}={26}^2\cdot{10}^3=676\cdot100=67.600\)
Resposta Questão 2
Alternativa C
Sabemos que existem 5 algarismos que são números pares. Assim, deve-se calcular o arranjo com repetição entre 5 elementos tomados de 4 em 4:
\(AR_{5,4}=5^4=625\)
Resposta Questão 3
Alternativa D
Sabemos que a data é 02/11, logo, a senha pode conter os algarismos 0, 1 e 2.
Se a senha contém 4 algarismos, então esse é um arranjo com repetição de 3 elementos tomados de 4 em 4.
\(AR_{3,4}=3^4=81\)
Resposta Questão 4
Alternativa D
Calcularemos o arranjo com repetição de 3 elementos tomados de 6 em 6:
\(AR_{3,6}=3^6=729\)
Resposta Questão 5
Alternativa B
Podemos perceber que se trata de um arranjo com repetição de 4 elementos tomados de 3 em 3. Substituindo na fórmula, temos que:
\(AR_{4,3}=4^3\)
Resposta Questão 6
Alternativa E
Calcularemos cada possibilidade, na busca daquela que contém como resposta um número entre 1 milhão e 2 milhões. Para facilitar, usaremos notação científica, pois sabemos que:
1 milhão = 106
2 milhões = 2 ⋅ 106
I → LDDDDD
\(26\ \cdot\ 105\ \ =\ 2,6\cdot{10}^6\)
Esse número é maior que 2 milhões, logo, não satisfaz o pedido da empresa.
II → DDDDDD
106 é igual a 1 milhão, logo, não satisfaz o pedido da empresa.
III → LLDDDD
\({26}^2·104=676⋅104=6,76⋅106\)
Esse número é maior que 2 milhões, logo, não satisfaz o pedido da empresa.
IV → DDDDD
105 é menor que 1 milhão, logo, não satisfaz o pedido da empresa.
V → LLLDD
\({26}^3·102=17576⋅102=1,7576⋅106\)
Esse número está entre 1 milhão e 2 milhões, logo, esse modelo de senha é o ideal.
Resposta Questão 7
Alternativa A
Nesse caso, o que ocorre é um arranjo com repetição entre os números 0 e 1 tomados de 3 em 3. Note que a ordem é importante e que os números apresentados possuem como algarismos 0 ou 1 ou ambos.
Resposta Questão 8
Alternativa D
Como há 2 possibilidades para cada símbolo (destacado ou não destacado), o total de possibilidades é um arranjo com repetição de 2 elementos tomados de 6 em 6. Logo, temos que:
\(AR_{2,6}=2^6\ =\ 64\)
Porém, sabemos que pelo menos um dos símbolos deve estar destacado, portanto é necessário subtrair 1 da resposta, pois a opção em que todos os símbolos não estão destacados não conta como um caractere.
64 – 1 = 63
Então, há um total de 63 caracteres possíveis.
Resposta Questão 9
Alternativa C
Entre 5 símbolos, escolheremos 3, sendo que um mesmo símbolo pode ser escolhido mais de uma vez. Isso se trata, então, de um arranjo com repetição de 5 elementos tomados de 3 em 3:
\(N\ =\ AR_{5,3}=5^3\)
Resposta Questão 10
Alternativa D
Trata-se de 3 indivíduos, e cada um poderá escolher 1 dentre 10 sabores. Portanto, o número de possibilidades de escolhas distintas é um arranjo com repetição de 10 elementos tomados de 3 em em 3.
\(AR_{10,3}={10}^3=1000\)
Resposta Questão 11
Alternativa B
Existem 5 classificações distintas para o atendimento, assim, calcularemos o arranjo com repetição de 5 elementos tomados de 20 em 20.
\(AR_{5,20}=5^{20}\)
Resposta Questão 12
Alternativa A
Na nova senha, há letras maiúsculas e minúsculas, ou seja, há \( 26\ \cdot2\ =52\) opções de letras, mais 10 opções de algarismos. Logo, para cada dígito escolhido, há 62 possibilidades. Como escolheremos 6 dígitos para a senha, trata-se de um arranjo com repetição, e a quantidade de senhas possíveis agora será de \({62}^6\). Na senha anterior, havia somente a opção de 10 algarismos para cada um dos 6 dígitos, assim, havia \({10}^6\) possibilidades. A razão então entre os dois tipos de senha é:
\(\frac{{62}^6}{{10}^6}\)



