Questão 4
(Ufpe 96) Num círculo, inscreve-se um quadrado de lado 7 cm. Sobre cada lado do quadrado, considera-se a semicircunferência exterior ao quadrado com centro no ponto médio do lado e raio 3,5cm, como na figura a seguir. Calcule a área da região hachurada.
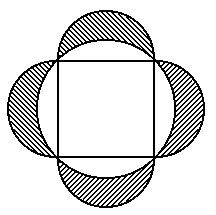
Apesar de parecer difícil, esse exercício exige apenas que você saiba calcular a área do quadrado e do círculo. Todo o trabalho pode ser feito em três passos:
I- calcular a área limitada pelos semicírculos hachurados;
II- calcular a área do círculo e
III- diminuir o resultado da primeira área pelo resultado da segunda.
Resposta Questão 1
Basta utilizar a fórmula para área do círculo:
A = π·r2
A = 3,14 · 72
A = 3,14 · 49
A = 153,86 cm2
Resposta Questão 2
Utilizando a fórmula da área do círculo, substitua o valor do raio e realize os cálculos:
A = π·r2
A = 3,14 · 92
A = 3,14 · 81
A = 254,34 cm2
Repare que o valor utilizado para o raio foi 9 cm e não 18 cm. Isso acontece porque 18 cm é o comprimento do diâmetro e não do raio. Uma vez que o raio é metade do diâmetro, basta fazer a substituição correta na fórmula.
Resposta Questão 3
Como o quadrado está inscrito no círculo, encontrando sua diagonal encontraremos também o diâmetro do círculo:
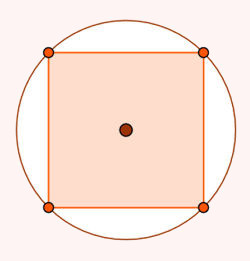
d = l√(2)
d = 4√(2)
O raio de um círculo é metade de seu diâmetro, portanto, r = 2√(2)
Agora, basta calcular a área desse círculo.
A = π·r2
A = 3,14 · [2√(2)]2
A = 3,14 · 4 · 2
A = 25,15 cm2
Resposta Questão 4
I- A figura abaixo representa a área limitada pelos semicírculos. Para calculá-la é preciso calcular a área do quadrado e somar com a área dos quatro semicírculos.

O lado do quadrado mede 7 cm. Sua área, portanto, é
Aq = l2 = 72 = 49 cm2
Agora, basta calcular a área de um semicírculo e multiplicar por 4, já que temos 4 deles no exercício.
As = π · r2
2
As = 3,14 · 3,52
2
As = 38,465
2
As = 19,2325 cm2
Para descobrir a área dos quatro semicírculos, basta multiplicar a área do semicírculo por 4
4*As = 19,2325 · 4
4*As = 76,93 cm2
Portanto, a área delimitada pelos semicírculos é a área dos semicírculos somada à área do quadrado:
A = 76,93 + 49 = 125,93 cm²
II- Para calcular a área do círculo é necessário saber seu raio, que é metade da diagonal do quadrado.
d = l ·√(2) = 7·√(2) = 9,9 cm
O raio do círculo é metade da diagonal do quadrado:
d = 9,9 = 4,95 cm
2 2
Com o raio do círculo em mãos, calcule sua área:
Ac = π·r2
Ac = 3,14 · 4,952
Ac = 3,14 · 24,5
Ac = 76,93 cm2
III- Basta finalizar o exercício diminuindo a área da região limitada pelos semicírculos pela área do círculo.
A – Ac = 125,93 – 76,96 = 49 cm²



