Questão 1
Duas retas se cruzam no vértice V, formando ângulos opostos pelo vértice medindo 6x + 9 e 9x – 9. Então, podemos afirmar que x é igual a:
A) 50º
B) 45º
C) 12º
D) 10º
E) 6º
Questão 2
Sabendo que os ângulos α e ꞵ são opostos pelo vértice, sabendo que α = 5x – 10 e ꞵ = 4x + 4, então, o valor do ângulo suplementar de ꞵ é igual a:
A) 120º
B) 90º
C) 60º
D) 45º
E) 30º
Questão 3
Analisando a imagem a seguir, podemos afirmar que os ângulos α e ꞵ são:
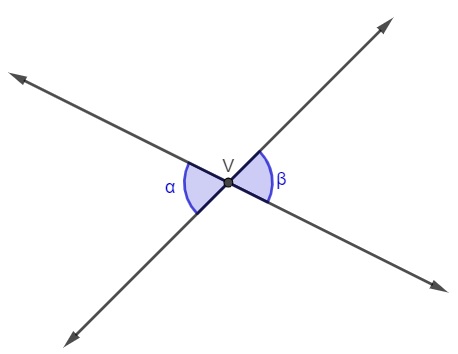
A) congruentes
B) suplementares
C) complementares
D) replementares
E) adjacentes
Questão 4
Analise a imagem a seguir:
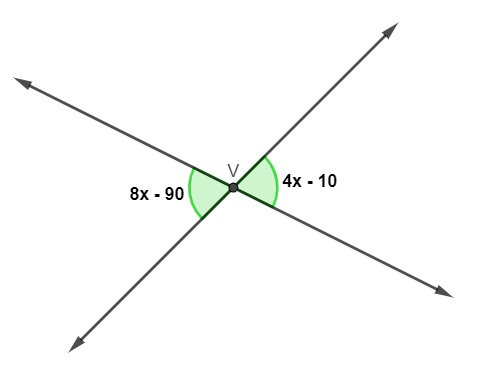
Podemos afirmar que o valor de x é:
A) 10º
B) 15º
C) 20º
D) 25º
E) 30º
Questão 5
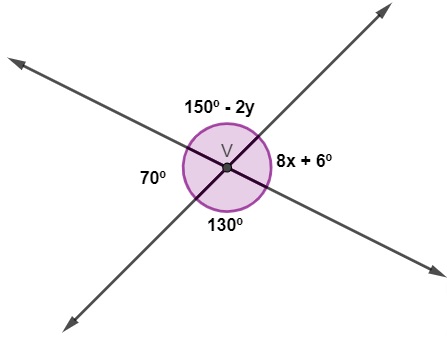
Analisando a imagem a seguir, a diferença entre y e x é igual a:
A) 0
B) 1
C) 2
D) -1
E) -2
Questão 6
(IFMA) Considerando-se que os ângulos 5x – 40º e 3x – 10º são opostos pelo vértice, o complemento de um desses ângulos mede:
A) 55º
B) 75º
C) 145º
D) 65º
E) 155º
Questão 7
Na imagem a seguir, estão destacados os ângulos a, b, c e d; analisando-a, podemos afirmar que:
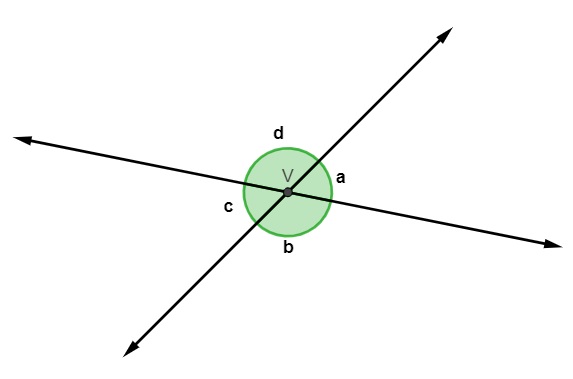
A) a e b são complementares.
B) c e a são suplementares.
C) b e c são opostos pelo vértice.
D) d e b são congruentes.
E) d e a são replementares.
Questão 8
Dois ângulos opostos pelo vértice medem 6x + 5 e 8x – 10, assim, a medida da soma desses ângulos é igual a:
A) 10º
B) 15º
C) 50º
D) 90º
E) 100º
Questão 9
Sobre as relações entre os ângulos, julgue as afirmativas a seguir:
I → Ângulos opostos pelo vértice são sempre congruentes.
II → Dois ângulos opostos pelo vértice não podem ser complementares.
III → Dois ângulos são replementares se a soma deles é igual a 360º.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Questão 10
Analise a imagem a seguir:
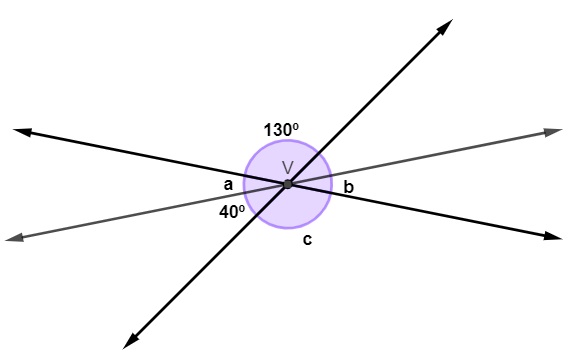
Podemos afirmar que o valor de a + b + c é igual a:
A) 130º
B) 140º
C) 150º
D) 160º
E) 180º
Questão 11
Analise a imagem a seguir:
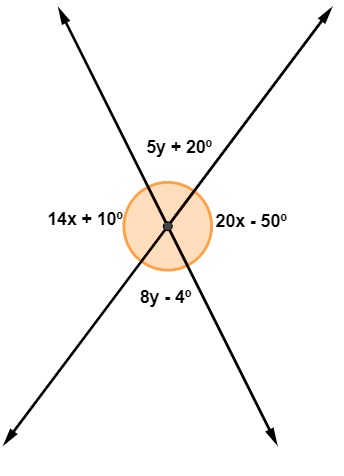
O valor da soma x + y é igual a:
A) 8º
B) 9º
C) 10º
D) 18º
E) 20º
Questão 12
O ângulo γ é complementar ao ângulo α, e o ângulo α é oposto pelo vértice ao ângulo ꞵ. Sabendo a medida de α = 3x + 10º e ꞵ = 5x – 16º, então, o valor do ângulo γ é:
A) 49º
B) 41º
C) 90º
D) 131º
E) 264º
Resposta Questão 1
Alternativa E
Como os ângulos são opostos pelo vértice, então, temos que:
9x – 9 = 6x + 9
9x – 6x = 9 + 9
3x = 18
x = 18 : 3
x = 6
Resposta Questão 2
Alternativa A
Sabemos que α e ꞵ são opostos pelo vértice, o que faz com que eles sejam congruentes, logo, temos que:
5x – 10 = 4x + 4
5x – 4x = 10 + 4
x = 14
Se x = 14, então, ꞵ = 4 ·14 + 4 = 56 + 4 = 60º.
O ângulo suplementar de ꞵ é o ângulo y tal que ꞵ + y = 180º:
60º + y = 180º
y = 180º – 60º
y = 120º
Resposta Questão 3
Alternativa A
Os ângulos da imagem são opostos pelo vértice, e ângulos opostos pelo vértice são sempre congruentes.
Resposta Questão 4
Alternativa C
Como os ângulos são opostos pelo vértice, então, temos que:
8x – 90 = 4x – 10
8x – 4x = -10 + 90
4x = 80
x = 80 : 4
x = 20º
Resposta Questão 5
Alternativa C
Sabemos que ângulos opostos pelo vértice são congruentes, então, para encontrar o valor de x, temos que:
8x + 6 = 70
8x = 70 – 6
8x = 64
x = 64 : 8
x = 8
Agora encontraremos o valor de y:
150 – 2y = 130º
150 – 130 = 2y
20 = 2y
y = 20 : 2
y = 10
A diferença entre y e x = 10 – 8 = 2.
Resposta Questão 6
Alternativa A
Como os ângulos são opostos pelo vértice, então, eles são congruentes:
5x – 40 = 3x – 10
5x – 3x = 40 – 10
2x = 30
x = 30 : 2
x = 15
Se x = 15, então, o ângulo mede 3 · 15 – 10 = 45 – 10 = 35.
Seja y o ângulo complementar ao ângulo de 35º, temos que:
y + 35 = 90
y = 90 – 35
y = 55º
Resposta Questão 7
Alternativa D
Os ângulos d e b são opostos pelo vértice e, portanto, são congruentes.
Resposta Questão 8
Alternativa E
Como os ângulos são opostos pelo vértice, então, eles são congruentes, logo, temos que:
8x – 10 = 6x + 5
8x – 6x = 10 + 5
2x = 15
x = 15 : 2
x = 7,5
Como os ângulos são iguais, vamos substituir o valor de x em um deles, e encontrar a medida de ambos.
6x + 5 = 6 · 7,5 + 5 = 45 + 5 = 50
Assim, ambos medem 50º, logo, 50 + 50 = 100º.
Resposta Questão 9
Alternativa B
I → Ângulos opostos pelo vértice são sempre congruentes. (verdadeira)
Sempre que houver ângulos opostos pelo vértice, eles serão congruentes.
II → Dois ângulos opostos pelo vértice não podem ser complementares. (falsa)
Não há restrição para a medida dos ângulos opostos, então, eles podem ter 45º e ser congruentes.
III → Dois ângulos são replementares se a soma deles é igual a 360º. (verdadeira)
Por definição, ângulos replementares somam 360º.
Resposta Questão 10
Alternativa C
Note que o ângulo com a medida c é oposto ao ângulo de 130º, então, temos que:
c = 130º
Podemos observar que os ângulos de 40º, 130º e a pertencem a uma mesma reta, ou seja, são suplementares.
a + 130º + 40º = 180º
a + 170º = 180º
a = 180º – 170º
a = 10º
Os ângulos a e b são opostos, logo, são congruentes:
b = 10º
A soma a + b + c = 130 + 10 + 10 = 150º.
Resposta Questão 11
Alternativa D
Igualando os ângulos opostos pelo vértice para encontrar o valor de x, temos que:
20x – 50º = 14x + 10º
20x – 14x = 50º + 10º
6x = 60º
x = 60º : 6
x = 10º
Agora, para calcular o valor de y, temos que:
8y – 4º = 5y + 20º
8y – 5y = 20º + 4º
3y = 24º
y = 24º : 3
y = 8º
A soma x + y = 10º + 8º = 18º.
Resposta Questão 12
Alternativa B
Como α e ꞵ são opostos pelo vértice, então, eles são congruentes, logo, temos que:
5x – 16º = 3x + 10º
5x – 3x = 10º + 16º
2x = 26º
x = 26º : 2
x = 13º
Como x = 13º, então, α = 3 · 13º + 10º = 49º.
Como γ é complementar a α, temos que:
α + γ = 90º
49º + γ = 90º
γ = 90º – 49º
γ = 41º



