Questão 1
A respeito das propriedades dos ângulos alternos internos e externos, assinale a alternativa correta:
a) Ângulos alternos internos são adjacentes.
b) Ângulos alternos internos são suplementares.
c) Ângulos adjacentes são congruentes.
d) Ângulos alternos externos são suplementares.
e) Ângulos alternos externos são congruentes.
Questão 2
Dadas as retas paralelas cortadas por uma transversal a seguir, calcule os valores dos ângulos a e b.
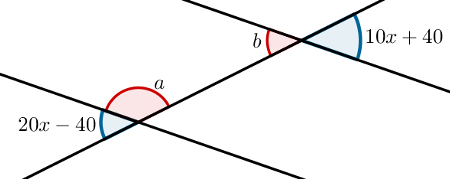
a) a = 60° e b = 120°
b) b = 60° e a = 120°
c) a = 60° e b = 60°
d) a = 120° e b = 120°
e) a = 90° e b = 90°
Questão 3
(UFES) Uma transversal intercepta duas paralelas formando ângulos alternos internos expressos em graus por (5x + 8) e (7x – 12). A soma das medidas desses ângulos é:
a) 40°
b) 58°
c) 80°
d) 116°
e) 150°
Questão 4
Dadas as retas paralelas cortadas por uma transversal a seguir, calcule a + b.
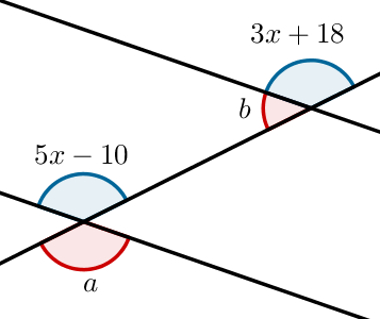
a) 14°
b) 60°
c) 120°
d) 180°
e) 200°
Resposta Questão 1
a) Incorreta!
Ângulos alternos internos são congruentes.
b) Incorreta!
Ângulos suplementares são aqueles cuja soma é igual a 180°. Essa propriedade não é garantida para ângulos alternos internos.
c) Incorreta!
Ângulos adjacentes são suplementares, e não congruentes.
d) Incorreta!
Ângulos alternos externos não são suplementares, e sim congruentes.
e) Correta!
Gabarito: Letra E.
Resposta Questão 2
Observe que os ângulos em azul são alternos externos. A propriedade para eles é de que ângulos alternos externos são congruentes, por isso, podemos escrever:
20x – 40 = 10x + 40
20x – 10x = 40 + 40
10x = 80
x = 80
10
x = 8
A medida de cada um desses ângulos é:
10x + 40 = 10·8 + 40 = 80 + 40 = 120°
O ângulo b é oposto pelo vértice, por isso, mede 120°. O ângulo a é adjacente, por isso, é suplementar a 120°. Logo, a = 60°.
Gabarito: Letra A.
Resposta Questão 3
Como o texto da questão já diz que os ângulos são alternos internos, não é necessário fazer desenho algum. A propriedade desses ângulos diz o seguinte: ângulos alternos internos são congruentes, logo:
5x + 8 = 7x – 12
5x – 7x = – 12 – 8
– 2x = – 20
2x = 20
x = 20
2
x = 10
Cada ângulo interno, portanto, mede:
5x + 8 = 5·10 + 8 = 50 + 8 = 58°
Como o exercício quer a soma dos dois ângulos,
58 + 58 = 116°
Gabarito: Letra D.
Resposta Questão 4
Observe que a é oposto pelo vértice a 5x – 10 e é alterno externo a 3x + 18. Dessa forma, podemos concluir que 5x – 10 é alterno externo a 3x + 18. Assim, podemos escrever:
5x – 10 = 3x + 18
5x – 3x = 18 + 10
2x = 28
x = 28
2
x = 14
Cada ângulo azul mede:
5x – 10 = 5·14 – 10 = 70 – 10 = 60°
Como a é oposto pelo vértice a 60°, a = 60°. Como b é adjacente a 60°, b é suplementar a 60°, logo, b = 120°. A soma a + b é:
a + b = 60 + 120 = 180°
Gabarito: Letra D.



