Questão 1
Joaquim deu 3/25 avos de sua herança para uma instituição de caridade.
a) Que fração representa a parcela da herança que sobrou para Joaquim?
b) Supondo que essa herança é de R$ 100000,00, quanto Joaquim doou?
Questão 2
Lucas gastou 25% de sua mesada com cinema e 22% também de sua mesada com consertos de sua bicicleta. Qual é a fração da mesada restante de Lucas?
Questão 3
(UNIFAP AP/2015) Considerando que R é o conjunto dos números reais, QC é o conjunto dos números irracionais, Q é o conjunto dos números racionais, Z é o conjunto dos números inteiros, N é o conjunto de números naturais e que 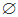 é o conjunto vazio. Qual alternativa abaixo é a correta?
é o conjunto vazio. Qual alternativa abaixo é a correta?
.jpg)
Questão 4
(FGV /2016) Na reta numérica indicada a seguir, todos os pontos marcados estão igualmente espaçados.

Sendo assim, a soma do numerador com o denominador da fração irredutível que representa x é igual a
a) 39.
b) 40.
c) 41.
d) 42.
e) 43.
Resposta Questão 1
a) Existem duas maneiras de calcular a parcela que restou para Joaquim:
Primeira maneira: Realizando a subtração:
1 – 3
25
Sabendo que o denominador da primeira fração é 1 e que o MMC entre 25 e 1 é o próprio 25, basta realizar os cálculos seguintes:
1 – 3 = 25 – 3 = 22
25 25 25 25
Então, a fração da herança restante é:
22
25
Segunda maneira: Basta pensar que a herança foi dividida em 25 partes, das quais 3 foram doadas para uma instituição de caridade. Logo, restaram 22 partes das 25, o que constitui a fração acima.
Resposta Questão 2
Porcentagens são frações de denominador 100, portanto, as frações gastas por Lucas são:
25 e 22
100 100
Logo, para calcular a fração restante da mesada de Lucas, basta somar essas duas frações e subtrair o resultado de 1, que representa o todo quando o assunto é porcentagem. Observe:
25 + 22 = 47
100 100 100
47 – 1 = 47 – 100 = 53
100 1 100 100
Lembrando que a soma das duas frações foi feita apenas nos numeradores, pois ela envolve denominadores iguais. A subtração envolve denominadores diferentes, portanto, é necessário fazer o MMC entre eles, dividir o MMC pelo denominador da segunda fração e multiplicar o resultado pelo seu numerador. Depois disso, repetir o processo para a segunda fração e realizar os cálculos como foi feito acima.
Resposta Questão 3
a) Falsa!
Q é o conjunto dos números que podem ser escritos na forma de fração. 2,5 é um número racional por esse motivo, mas não é uma fração.
b) Falsa!
O conjunto dos números irracionais não contém nem está contido no conjunto dos números racionais. Na realidade, não existe nenhum número no conjunto dos números reais que seja racional e irracional simultaneamente.
c) Falsa!
2 é um número racional, por isso, não pode ser irracional.
d) Verdadeira!
Como dito anteriormente, não existe um só elemento que pertença simultaneamente ao conjunto dos números racionais e irracionais. A simbologia dessa questão está dizendo justamente isto. Para tanto, leia essa simbologia da seguinte maneira: A intersecção entre racionais e irracionais é igual ao conjunto vazio.
e) Falsa!
O conjunto dos números reais não é subconjunto dos números racionais, mas, sim, o contrário. Portanto, é o conjunto dos números racionais que está contido no conjunto dos números reais.
Alternativa D.
Resposta Questão 4
O comprimento de cada um dos quatro segmentos é dado pela divisão do segmento que vai de 3/7 a 4/7 dividido por 4. Para tanto, calcule a diferença entre esses dois pontos e divida o resultado por 4. Para esse primeiro cálculo, a subtração envolve frações com denominadores iguais, portanto, basta subtrair os denominadores.
4 – 3 = 1
7 7 7
1 : 4
7
1 · 1 = 1
7 4 28
Tendo em mãos esse resultado, some-o ao primeiro valor para encontrar o valor de x. Nessa etapa, calcule o mínimo múltiplo comum entre os denominadores e calcule os novos numeradores da seguinte maneira: Divida o MMC pelo denominador da primeira fração e multiplique o resultado pelo numerador dessa mesma fração. Repita o procedimento para a segunda fração e obtenha os resultados seguintes:
1 + 3 = 1 + 12 = 13
28 7 28 28
Feito isso, some o numerador e o denominador de x, como propõe o final do exercício:
13 + 28 = 41
Alternativa C.



