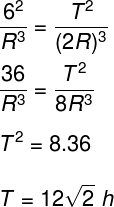Questão 1
Um satélite artificial encontra-se em equilíbrio em uma órbita circular em torno da Terra. Dobrando-se a massa desse satélite, é esperado que o raio r de sua órbita:
a) diminua pela metade.
b) permaneça inalterada.
c) aumente para 2r.
d) diminua para r/4.
e) aumente para 4r.
Questão 2
Um satélite em uma órbita de raio R completa uma volta em torno da Terra a cada seis horas. Se o mesmo satélite fosse colocado a uma distância 2R da Terra, seu período orbital seria igual a:
a) √2 h
b) 16√2 h
c) 12√2 h
d) 4√2 h
e) 2 h
Questão 3
O movimento de um satélite, natural ou artificial, em órbita no planeta Terra é completamente descrito por meio:
a) do sistema heliocêntrico, proposto por Nicolau Copérnico.
b) da mecânica de Galileu.
c) das três leis de Kepler.
d) da Lei da Gravitação Universal, de Isaac Newton.
e) do sistema geocêntrico, de Ptolomeu.
Questão 4
Em relação à Gravitação Universal e às leis de Kepler, assinale a alternativa correta entre os itens abaixo:
a) Dois satélites de massas diferentes apresentarão velocidades orbitais diferentes em relação a um mesmo astro.
b) Dois satélites, independentemente de suas massas, terão a mesma velocidade em relação à Terra se apresentarem o mesmo raio orbital.
c) A força que a Terra faz sobre um de seus satélites, seja ele artificial ou natural (como a Lua), é maior que a força que esses satélites farão sobre a Terra.
d) Quanto maior a inércia do satélite, menor será sua velocidade orbital.
Resposta Questão 1
Letra B
A velocidade orbital de um satélite em equilíbrio, seja ele artificial ou natural, é dada pela equação a seguir:
Na equação mostrada acima, v é a velocidade do satélite em m/s, G é a Constante de Gravitação Universal, M é a massa do planeta (no caso, a Terra) e r é o raio da órbita do satélite.
Logo, é possível perceber que essas variáveis não dependem da massa do satélite, mas da massa do planeta. Portanto, caso a massa do satélite fosse duplicada, sua órbita permaneceria inalterada.
Resposta Questão 2
Letra C
De acordo com a terceira lei de Kepler, sabemos que o quadrado do período orbital dos corpos dividido pelo cubo dos raios médios de suas órbitas, quando em torno do mesmo astro, é igual para todos satélites de determinado astro.
Sendo assim, podemos igualar as constantes para dois satélites movendo-se em torno do mesmo astro:
Resposta Questão 3
Letra D
Apesar de as três leis de Kepler conseguirem prever o formato das órbitas e a relação entre período e raio orbital, algumas informações adicionais são calculadas por meio da Lei da Gravitação Universal, desenvolvida por Isaac Newton. Essa lei é, portanto, uma generalização daquelas leis propostas por Johannes Kepler.
Resposta Questão 4
Letra B
a) FALSO – A velocidade orbital dos satélites depende inversamente da raiz quadrada da distância em relação ao planeta ou ao astro que orbitem, e depende também da massa desse astro multiplicada pela constante de gravitação universal. Logo a velocidade independe da massa dos satélites.
b) VERDADEIRO – A velocidade orbital dos satélites independe de suas massas, e seu módulo pode ser calculado por meio da seguinte equação:
c) FALSO – A força gravitacional que a Terra faz sobre seus satélites tem módulo igual à força que seus satélites exercem sobre ela. Isso está de acordo com a terceira lei de Newton, princípio da ação e reação.
d) FALSO – De acordo com as leis de Newton, a massa é uma expressão da inércia. Ao olharmos para a equação mostrada na correção da letra B, veremos que não há dependência da velocidade do satélite com a própria massa, somente com a massa da Terra.