Questão 1
(IF-GO) O móbile é um modelo abstrato que tem peças móveis, impulsionadas por motores ou pela força natural das correntes de ar. Suas partes giratórias criam uma experiência visual de dimensões e formas em constante equilíbrio. O móbile foi inicialmente sugerido por Marcel Duchamp para uma exibição de 1932, em Paris, sobre certas obras de Alexander Calder, que se converteu no maior exponente da escultura móbile. A origem latina do termo móbile remete à ideia de "móbil", "movimento". A figura a seguir representa um tipo de móbile.
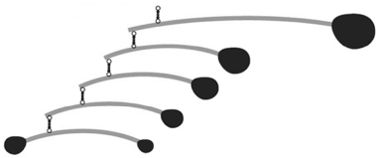
Para que o equilíbrio do móbile ocorra, é necessário e suficiente que
a) as massas penduradas nas extremidades de cada haste sejam iguais.
b) a força resultante e o torque sobre cada uma das hastes sejam nulos.
c) a força resultante sobre cada haste seja nula.
d) o torque jamais seja nulo.
e) haja conservação da energia mecânica.
Questão 2
(FCM-PB) O guindaste (também chamado de grua e, nos navios, pau de carga) é um equipamento utilizado para a elevação e a movimentação de cargas e materiais pesados, assim como a ponte rolante a partir do princípio da física no qual uma ou mais máquinas simples criam vantagem mecânica para mover cargas além da capacidade humana. São comumente empregados nas indústrias, terminais portuários e aeroportuários, onde se exige grande mobilidade no manuseio de cargas e transporte de uma fonte primária à embarcação, trem ou elemento de transporte primário, ou mesmo avião, para uma fonte secundária, um veículo de transportes ou depósitos locais. Podem descarregar e carregar contêineres, organizar material pesado em grandes depósitos, movimentação de cargas pesadas na construção civil e as conhecidas pontes rolantes ou guindastes móveis muito utilizados nas indústrias de laminação e motores pesados.
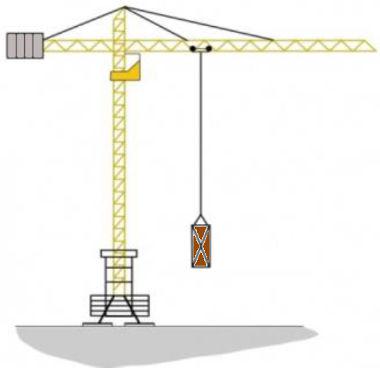
Um aluno, de posse de um simulador, projeta a Grua acima com as seguintes características: o braço maior da Grua tem comprimento de 16 metros, o braço menor, 4 m; o contrapeso na extremidade do braço menor tem uma massa equivalente a 0,5 toneladas, cujo centro de massa coincide com a extremidade do braço menor. A barra horizontal possui massa de 200 kg, uniformemente distribuída, e a barra vertical está rigidamente fixada. De acordo com o projeto acima descrito, qual o peso máximo que essa Grua poderá levantar sem tombar?
a) 2000N
b) 1500N
c) 1000N
d) 50N
e) 500N
Questão 3
Dois garotos brincam em uma gangorra de 10 m de comprimento que possui seu eixo de rotação exatamente em seu centro. Adotando a barra que compõe a gangorra como homogênea e sabendo que um garoto de 30 kg sentou-se na extremidade da direita, qual deverá ser a distância entre o segundo garoto e o eixo de rotação para que a gangorra mantenha-se em equilíbrio.
Dados: Massa do segundo garoto = 40 kg; Aceleração da gravidade = 10 m/s2.
a) 3,75
b) 3,50
c) 4,75
d) 4,27
e) 1,20
Questão 4
Analise as afirmações a respeito do momento de uma força.
I) O torque é uma grandeza escalar relacionada com a rotação de um sistema.
II) A força necessária para girar uma porta seria maior se a maçaneta fosse instalada próximo das dobradiças.
III) A única condição de equilíbrio existente está relacionada com a rotação de um sistema. Sendo assim, se a soma de todos os torques que atuam em um sistema for nula, haverá equilíbrio.
Está correto o que se afirma em:
a) I e II
b) II e III
c) III
d)II
e) I
Resposta Questão 1
Letra B
As condições para que um corpo esteja em equilíbrio são a soma nula de todas as forças e de todos os torques.
Resposta Questão 2
Letra E
Adotando o ponto de encontro das barras vertical e horizontal como o eixo de rotação, os braços de alavanca de cada uma das forças serão:
Contrapeso = 4 m
Peso da barra horizontal = 6 m. Como o peso distribui-se de forma homogênea, podemos considerar o centro de massa da barra exatamente em seu centro, assim, a posição do peso da barra é 10 m de qualquer uma das extremidades. Em relação ao eixo de rotação, a distância é de apenas 6 m.
Peso máximo erguido pela grua = 16 m. Para determinar o máximo peso suportado pela grua, devemos colocar o peso na extremidade da máquina.
Sabendo que a força peso é o produto da massa de um elemento pelo valor da gravidade, temos:
Contrapeso: 500 kg. 10 m/s2 = 5000 N
Peso da Barra: 200 kg .10 m/s2 = 2000 N
Adotando o sentido horário como positivo e sabendo que o torque é o produto da força pelo braço de alavanca, teremos:
τPMÁX + τPB – τCP = 0
τPMÁX = Torque do peso máximo;
τPB = Torque do peso da barra;
τCP = Torque do contrapeso.
P.16 + 2000.6 – 5000 .4 = 0
16.P = 20000 – 12000
16.P = 8000
P = 8000 ÷ 16
P = 500 N.
O peso máximo a ser erguido pela grua é de 500 N.
Resposta Questão 3
Letra A
Para que o equilíbrio seja possível, os torques gerados pelo peso de cada garoto deverão ser iguais. Sabendo que o peso é fruto do produto da massa pela aceleração da gravidade e que o torque é o produto da força pelo braço de alavanca (X), podemos escrever que:
40.10.X = 30.10 .5
400.X = 1500
X = 3,75 m
Resposta Questão 4
Letra D
I) Errada. O torque é uma grandeza vetorial.
II) Correta. Quanto maior for a distância entre o ponto de aplicação da força e o eixo de rotação, menor será o esforço necessário para que o sistema rotacione.
III) Errada. A soma dos torques e a soma das forças devem ser nulas.



