Questão 1
Um objeto desloca-se com momento linear igual a 50 kg.m/s, mas choca-se com uma parede e gasta 0,02 s para parar. Por meio do teorema do impulso, determine o valor da força necessária para parar esse objeto.
a) 1000 N
b) 1500 N
c) 2000 N
d) 2500 N
e) 3000 N
Questão 2
Um carro de massa igual a 1200 Kg desloca-se com velocidade igual a 36 km/h. Quando o motorista acelera o veículo, passa a se movimentar com velocidade igual a 54 Km/h. Se o tempo gasto para mudança de velocidade foi de 2 s, determine a força resultante que agiu sobre o veículo.
a) 6000 N
b) 5000 N
c) 4000 N
d) 3000 N
e) 2000 N
Questão 3
(Unicamp-2013) Muitos carros possuem um sistema de segurança para os passageiros chamado airbag. Este sistema consiste em uma bolsa de plástico que é rapidamente inflada quando o carro sofre uma desaceleração brusca, interpondo-se entre o passageiro e o painel do veículo. Em uma colisão, a função do airbag é
a) aumentar o intervalo de tempo de colisão entre o passageiro e o carro, reduzindo assim a força recebida pelo passageiro.
b) aumentar a variação de momento linear do passageiro durante a colisão, reduzindo assim a força recebida pelo passageiro.
c) diminuir o intervalo de tempo de colisão entre o passageiro e o carro, reduzindo assim a força recebida pelo passageiro.
d) diminuir o impulso recebido pelo passageiro devido ao choque, reduzindo assim a força recebida pelo passageiro.
Questão 4
(FGV) Um brinquedo muito simples de construir e que vai ao encontro dos ideais de redução, reutilização e reciclagem de lixo é retratado na figura.
A brincadeira, em dupla, consiste em mandar o bólido de 100 g, feito de garrafas plásticas, um para o outro. Quem recebe o bólido, mantém suas mãos juntas, tornando os fios paralelos, enquanto, aquele que o manda, abre com vigor os braços, imprimindo uma força variável, conforme o gráfico.
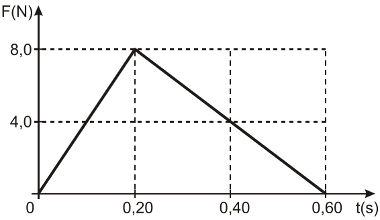
Considere que:
-
a resistência ao movimento causada pelo ar e o atrito entre as garrafas com os fios sejam desprezíveis;
-
o tempo que o bólido necessita para deslocar-se de um extremo ao outro do brinquedo seja igual ou superior a 0,60 s.
Dessa forma, iniciando a brincadeira com o bólido em um dos extremos do brinquedo, com velocidade nula, a velocidade de chegada do bólido ao outro extremo, em m/s, é de
a) 16
b) 20
c) 24
d) 28
e) 32
Resposta Questão 1
LETRA “D”
Aplicando o teorema do impulso, temos:
I = ΔQ
Como I = F.Δt, temos:
F.Δt = ΔQ
A variação da quantidade de movimento do objeto vai de 50 kg.m/s para zero, logo, podemos concluir que ΔQ = 50 Kg.m/s. Sendo assim, temos:
F.0,02 = 50
F.2x10 – 2 = 50
F = 50
2x10 – 2
F = 25 x 102
F = 2500 N
Resposta Questão 2
LETRA “D”
Aplicando o teorema do impulso, temos:
I = ΔQ
Como I = F.Δt e Q = m.v, temos:
F.Δt = mv – mv0
F.Δt = m (v – v0)
F = m (v – v0)
Δt
Transformando as velocidades, teremos: 54 km/h ÷ 3,6 = 15 m/s; 36 km/h ÷ 3,6 = 10 m/s, então:
F = 1200.(15 - 10)
2
F = 1200 . 5 = 600.5 = 3000 N
2
Resposta Questão 3
LETRA “A”
A partir do teorema do impulso, temos:
I = ΔQ
F.Δt = m.Δv
F= m.Δv
Δt
Por meio dessa última relação, podemos perceber que a força é inversamente proporcional ao intervalo de tempo, logo, a função do airbag é aumentar o intervalo de tempo de colisão entre o passageiro e o carro para reduzir a força recebida.
Resposta Questão 4
LETRA “C”
O impulso é numericamente igual à área do gráfico F x t. Como a figura geométrica que aparece no gráfico é um triângulo, temos:
I = base x altura
2
I = 0,6 . 8
2
I = 2,4 N.s
A determinação da velocidade de chegada do bólido será feita por meio do teorema do impulso:
I = ΔQ
I = m . Δv
I = m . (v – v0)
2,4 = 0,1 . (v – 0)
v = 2,4 / ,01
v = 24 m/s



