Questão 1
(VUNESP) Os valores nominais de uma lâmpada incandescente, usada em uma lanterna, são: 6,0 V; 20 mA. Isso significa que a resistência elétrica do seu filamento é de:
a) 150 Ω, sempre, com a lâmpada acesa ou apagada.
b) 300 Ω, sempre, com a lâmpada acesa ou apagada.
c) 300 Ω com a lâmpada acesa e tem um valor bem maior quando apagada.
d) 300 Ω com a lâmpada acesa e tem um valor bem menor quando apagada.
e) 600 Ω com a lâmpada acesa e tem um valor bem maior quando apagada.
Questão 2
(UEL) Um resistor de 10 Ω no qual flui uma corrente elétrica de 3,0 ampères está associado em paralelo com outro resistor. Sendo a corrente elétrica total, na associação, igual a 4,5 ampères, o valor do segundo resistor, em ohms, é:
a) 5,0
b) 10
c) 20
d) 30
e) 60
Questão 3
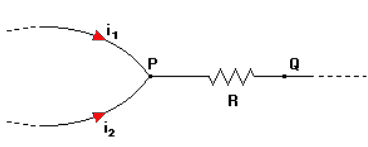
A figura abaixo mostra um resistor R de 40 Ω entre os pontos P e Q. As correntes i1 e i2 unem-se no ponto P e passam pelo resistor R. Sabendo que a diferença de potencial entre os pontos P e Q é de 200 V e que a intensidade da corrente i1 excede em uma unidade o triplo da intensidade da corrente i2, determine o valor das correntes elétricas i1 e i2, respectivamente.
a) 1,6 e 0,2
b) 7 e 2
c) 4 e 1
d) 2,5 e 0,5
e) 3,4 e 0,8
Questão 4
Determine a corrente elétrica que flui por um resistor de 1 kΩ quando ele é submetido a uma ddp de 200 V.
a) 0,5 A
b) 2 dA
c) 4 A
d) 0,02 A
e) 1 A
Resposta Questão 1
LETRA “D”
Aplicando a relação U = R . i, temos:
6 = R . 20 x 10 – 3
R = 6 ÷ 20 x 10 – 3
R = 300 Ω
A resistência é variável com o aumento de temperatura. Sendo assim, como a temperatura do filamento é bem menor quando a lâmpada está apagada, a resistência também é menor.
Resposta Questão 2
LETRA “C”
Aplicando a relação U = R . i, podemos descobrir a ddp à qual o resistor de 10 Ω está submetido.
U = R . i
U = 10 . 3 = 30 V
Nas associações em paralelo, os resistores possuem a mesma ddp e correntes diferentes. Como a corrente total é de 4,5 A e a corrente do resistor de 10 Ω é 3,0 A, podemos concluir que a corrente do segundo resistor é 1,5 A e a ddp à qual está submetido é de 30 V. Sendo assim, temos:
U = R . i
30 = R . 1,5
R = 20 Ω
Resposta Questão 3
LETRA “C”
Aplicando a equação U = R . i entre os pontos P e Q, teremos:
U = R. (i1 + i2)
Agora substituiremos os valores:
200 = 40. (i1 + i2)
(i1 + i2) = 200/40
(i1 + i2) = 5 A
A corrente i1 excede em uma unidade o triplo da corrente i2:
i1 = 3.i2 + 1
Logo,
i1 + i2 = 5 A
(3.i2 + 1) + i2 = 5
4.i2 + 1 = 5
4.i2 = 4
i2 = 1 A
Então,
i1 = 3.i2 + 1
i1 = 3.1 + 1
i1 = 4 A
Resposta Questão 4
LETRA “B”
Sabendo que 1 kΩ = 1000 Ω, temos:
U = R . i
200 = 1000 . i
i = 200/1000
i = 0,2 = 2,0 x 10 - 1
Como o prefixo multiplicativo “deci” equivale a 10 – 1, temos:
i = 2 dA



