Questão 1
Analise as alternativas abaixo referentes às unidades de medida estudadas no potencial elétrico:
I. A unidade de medida da carga elétrica é metro por segundo.
II. A unidade de medida do trabalho da força elétrica é Joule.
III. A unidade de medida do campo elétrico é Newton por Coulomb.
IV. A unidade de medida da energia potencial elétrica é Coulomb.
V. A unidade de medida do potencial elétrico é Volt.
Está(ão) correta(s):
A) Todas estão incorretas.
B) Todas estão corretas.
C) I, II e V.
D) I, III e IV.
E) II, III e V.
Questão 2
Qual o potencial elétrico em um ponto no vácuo distante a 0,4 metros de uma carga elétrica de 80∙10-10C?
Dado: \(k_o=9\cdot{10}^{9\ }{\left(N\cdot m\right)^2/C}^2\).
A) 200 V
B) 180 V
C) 360 V
D) 530 V
E) 470 V
Questão 3
Uma partícula com carga elétrica 120 mC produz um potencial elétrico de 48V e um campo elétrico de valor E. Analisando essas informações, encontre o valor do campo elétrico produzido.
A) 400 N/C
B) 4 N/C
C) 40 N/C
D) 0,4 N/C
E) 4000 N/C
Questão 4
Determine o potencial elétrico de uma partícula com carga elétrica de 35∙10-2 C que se desloca em uma região com campo elétrico, do ponto A até o B, sabendo que a força elétrica realizou um trabalho de 77 J para deslocar a partícula do ponto A até o B.
A) 0 V
B) 110 V
C) 220 V
D) 280 V
E) 150 V
Questão 5
Determine a diferença de potencial elétrico entre os terminais de um resistor de 250 Ω que é atravessado por uma corrente elétrica de 20 mA .
A) 1 V
B) 2 V
C) 3 V
D) 4 V
E) 5 V
Questão 6
Qual é a energia potencial de uma partícula de carga elétrica 0,2 C em um potencial elétrico de 110 V ?
A) 88 J
B) 59 J
C) 14 J
D) 22 J
E) 35 J
Questão 7
Determine o trabalho da força elétrica de uma partícula com carga elétrica de 10-2 C que sai de um ponto inicial com potencial 400 V para outro ponto com potencial de 150 V .
A) 15 000 J
B) 25 000 J
C) 55 000 J
D) 45 000 J
E) 40 000 J
Questão 8
Um campo elétrico de 640 N/C é produzido por uma carga elétrica de 20∙10-2 C. Da mesma forma, ela produzirá um potencial elétrico; assim, determine seu valor.
A) 64 V
B) 55 V
C) 190 V
D) 128 V
E) 210 V
Questão 9
(Uece) Uma esfera metálica maciça é carregada eletricamente com carga positiva.
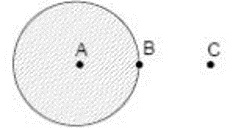
Considerando que o potencial no infinito é zero, podemos afirmar que os potenciais VA, VB e VC referentes, respectivamente, aos pontos A, B e C são, conforme sua intensidade,
A) VA < VB < VC
B) VA > VB =VC
C) VA = VB > VC
D) VA > VB > VC
Questão 10
(Uece) Uma carga de 15 nC pode ser produzida por simples atrito. A variação de potencial elétrico, em Volts, que essa carga causará em uma esfera condutora isolada de 16 cm de raio é, aproximadamente:
A) 844
B) 864
C) 444
D) 464
Questão 11
(Mackenzie) Uma partícula de massa 1 g , eletrizada com carga elétrica positiva de 40 µC , é abandonada do repouso no ponto A de um campo elétrico uniforme, no qual o potencial elétrico é 300 V . Essa partícula adquire movimento e se choca em B, com um anteparo rígido. Sabendo-se que o potencial elétrico do ponto B é de 100 V , a velocidade dessa partícula ao se chocar com o obstáculo é de
A) 4 m/s
B) 5 m/s
C) 6 m/s
D) 7 m/s
E) 8 m/s
Questão 12
(UFSM) Uma partícula com carga q=2∙10-7C se desloca do ponto A ao ponto B, que se localizam em uma região em que existe um campo elétrico. Durante esse deslocamento, a força elétrica realiza um trabalho igual a 4∙10-3 J sobre a partícula. A diferença de potencial UA-UB entre os dois pontos considerados vale, em V:
A) -8∙10-10
B) 8∙10-10
C) -2∙104
D) 2∙104
E) 0,5∙10-4
Resposta Questão 1
Alternativa E
I. A unidade de medida da carga elétrica é metro por segundo. (Falso)
A unidade de medida da carga elétrica é Coulomb.
II. A unidade de medida do trabalho da força elétrica é Joule. (Verdadeiro)
III. A unidade de medida do campo elétrico é Newton por Coulomb. (Verdadeiro)
IV. A unidade de medida da energia potencial elétrica é Coulomb. (Falso)
A unidade de medida da energia potencial elétrica é Joule.
V. A unidade de medida do potencial elétrico é Volt. (Verdadeiro)
Resposta Questão 2
Alternativa B
Encontraremos o potencial elétrico produzido por uma partícula carregada por meio da sua fórmula:
\(U=k_o\cdot\frac{Q}{d}\)
\(U=9\cdot{10}^{9\ }\cdot\frac{80\cdot{10}^{-10}}{0,4}\)
\(U=9\cdot{10}^{9\ }\cdot200\cdot{10}^{-10}\)
\(U=1800\cdot{10}^{9-10}\)
\(U=1800\cdot{10}^{-1}\)
\(U=180\cdot{10}^1\cdot{10}^{-1}\)
\(U=180\cdot{10}^{1-1}\)
\(U=180\cdot{10}^0\)
\(U=180\cdot1\)
\(U=180\ V\)
Resposta Questão 3
Alternativa A
Calcularemos o campo elétrico produzido pela carga elétrica utilizando a fórmula do potencial elétrico relacionado ao campo elétrico e à carga elétrica:
\(U=E\cdot q\)
\(48=E\cdot120\ m\)
O m significa mili, cujo valor é de 10-3 , então:
\(48=E\cdot120\cdot{10}^{-3}\)
\(E=\frac{48}{120\cdot{10}^{-3}}\)
\(E=0,4\cdot{10}^3\)
\(E=400\cdot{10}^{-3}\cdot{10}^3\)
\(E=400\cdot{10}^{-3+3}\)
\(E=400\cdot{10}^0\)
\(E=400\cdot1\)
\(E=400\ N/C\)
Resposta Questão 4
Alternativa C
Calcularemos o potencial elétrico no ponto A usando a sua fórmula que o relaciona ao trabalho da força elétrica com a carga elétrica:
\(U_A=\frac{W_{AB}}{q}\)
\(U_A=\frac{77}{35\cdot{10}^{-2}\ }\)
\(U_A=2,2\cdot{10}^2\)
\(U_A=220\ V\)
Resposta Questão 5
Alternativa E
Para encontrarmos a diferença de potencial elétrico em um resistor, usaremos a primeira lei de Ohm:
\(U=R\cdot i\)
\(U=250\cdot20\ m\)
O m em 20 mA significa micro, que vale 10-3 , então:
\(U=250\cdot20\cdot{10}^{-3}\ \)
\(U=5000\cdot{10}^{-3}\)
\(U=5\cdot{10}^3\cdot{10}^{-3}\)
\(U=5\cdot{10}^{3-3}\)
\(U=5\cdot{10}^0\)
\(U=5\cdot1\)
\(U=5\ V\)
Resposta Questão 6
Alternativa D
Calcularemos a energia potencial elétrica usando a fórmula que a relaciona à carga elétrica e ao potencial elétrico:
\(E_{pel}=q\cdot V\)
\(E_{pel}=0,2\cdot110\)
\(E_{pel}=22\ J\)
Resposta Questão 7
Alternativa B
Encontraremos o trabalho da força elétrica por meio da sua fórmula que a relaciona ao potencial elétrico:
\(∆U=-WFelq\)
\(U_B-U_A=-\frac{W_{Fel}}{q}\)
\(150-400=-\frac{W_{Fel}}{{10}^{-2}}\)
\(-250=-\frac{W_{Fel}}{{10}^{-2}}\)
\(250\cdot{10}^2=W_{Fel}\)
\(25\ 000\ J=W_{Fel}\)
Resposta Questão 8
Alternativa D
Calcularemos o potencial elétrico produzido pela carga elétrica usando a fórmula que o relaciona ao campo elétrico e à carga elétrica:
\(U=E\cdot q\)
\(U=640\cdot20\cdot{10}^{-2}\)
\(U=12\ 800\cdot{10}^{-2}\)
\(U=128\cdot{10}^2\ \cdot{10}^{-2}\)
\(U=128\cdot{10}^{2-2}\)
\(U=128\cdot{10}^0\)
\(U=128\cdot1\)
\(U=128\ V\)
Resposta Questão 9
Alternativa C
O potencial dentro e ao redor da esfera será o mesmo. Mas, como sabemos, o potencial elétrico é inversamente proporcional à distância, portanto quanto maior for a distância da esfera, menor será o potencial elétrico. Assim, o potencial em C será o menor de todos.
Resposta Questão 10
Alternativa A
Primeiramente, vamos converter a distância de centímetros para metros, obtendo:
\(16\ cm=0,16\ m\)
Então, calcularemos o potencial elétrico por meio da sua fórmula:
\(U=k\cdot\frac{Q}{d}\)
\(U=9\cdot{10}^9\cdot\frac{15\ n}{0,16}\)
O n significa nano, cujo valor é de 10-9 :
\(U=9\cdot{10}^9\cdot\frac{15\cdot{10}^{-9}}{0,16}\)
\(U=\frac{135\cdot{10}^{9-9}}{0,16}\)
\(U=\frac{135\cdot{10}^0}{0,16}\)
\(U=\frac{135\cdot1}{0,16}\)
\(U=843,75\ V\ \)
\(U\ \approx844\ V\)
Resposta Questão 11
Alternativa A
Primeiramente, vamos converter a massa de gramas para quilogramas:
\(1\ g=0,001\ kg\)
Para encontrarmos a velocidade dessa partícula, usaremos o teorema do trabalho e energia cinética:
\(W=∆E_{c}\)
Nesse caso, teremos o trabalho da força elétrica que transportará essa partícula do ponto A ao B:
\(W_{Fel}=∆E_{c}\)
\(-q\cdot∆U=E_{c final}-E_{c inicial}\)
\(-q\cdot(U_B-U_A)=E_{c final}-E_{c inicial}\)
Como a velocidade inicial é nula, a energia cinética inicial também será:
\(-q\cdot(U_B-U_A)=\frac{m\cdot v^2}{2}-0\)
\(-40\ µ\cdot(100-300)=\frac{0,001\cdot v^2}{2}\)
O µ significa micro, cujo valor é de 10-6 :
\(-40\cdot{10}^{-6}\cdot(100-300)=\frac{0,001\cdot v^2}{2}\)
\(-40\cdot{10}^{-6}\cdot(-200)=0,0005\cdot v^2\)
\(8\ 000\cdot{10}^{-6}=0,0005\cdot v^2\)
\(v^2=\frac{8\ 000\cdot{10}^{-6}}{0,0005}\)
\(v^2=16\ 000\ 000\cdot{10}^{-6}\)
\(v^2=16\cdot{10}^6\cdot{10}^{-6}\)
\(v^2=16\)
\(v=\sqrt{16}\)
\(v=4\ m/s\ \)
Resposta Questão 12
Alternativa D
Para encontrarmos a diferença de potencial UA - UB, usaremos a fórmula que a relaciona ao trabalho e à carga elétrica:
\(∆U=-W\frac{W_{Fel}}{q}\)
Temos que ∆U=UB-UA , então:
\(U_B-U_A=-\frac{W_{Fel}}{q}\)
\(U_B-U_A=-\frac{4\cdot{10}^{-3}}{2\cdot{10}^{-7}\ }\)
\(U_B-U_A=-2\cdot{10}^{-3+7}\)
\(U_B-U_A=-2\cdot{10}^4\)
Como o enunciado pede UA - UB, inverteremos desta forma:
\(-(U_A-U_B)=-2\cdot{10}^4\)
\((U_A-U_B)=2\cdot{10}^4\)



