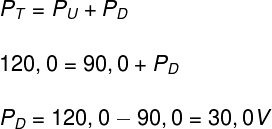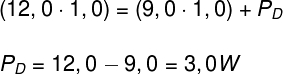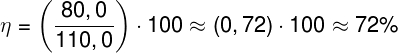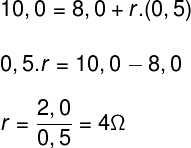Questão 1
A potência utilizada por um receptor, quando alimentado por uma fonte de tensão de 120,0 V, é igual a 90,0 V. Podemos dizer que a tensão dissipada por esse receptor é equivalente a:
a) 120,0 V
b) 210,0 V
c) 30,0 V
d) 90,0 V
e) 60,0 V
Questão 2
Um receptor elétrico de força contraeletromotriz igual a 9,0 V é ligado em uma tensão de 12,0 V e passa a ser percorrido por uma corrente elétrica de 1,0. A potência dissipada por esse receptor é igual a:
a) 12,0 W
b) 3,0 W
c) 21,0 W
d) 108 W
e) 9,0 W
Questão 3
Um receptor elétrico opera com força contraeletromotriz de 80,0 V quando ligado em uma rede de tensão elétrica igual a 110,0 V. O valor mais próximo de seu rendimento é de:
a) 95%
b) 90%
c) 65%
d) 80%
e) 72%
Questão 4
Um receptor cuja força contraeletromotriz é de 8,0 V é ligado em uma bateria de 10,0 V, estabelecendo-se sobre ele uma corrente elétrica de 0,5 A. A resistência interna desse receptor é igual a:
a) 2,0 Ω
b) 0,5 Ω
c) 4,0 Ω
d) 6,0 Ω
e) 3,0 Ω
Resposta Questão 1
Letra C
A potência total fornecida a um receptor é dada pela soma das potências dissipada e útil. Dessa forma, temos que:
Portanto, é correto afirmar que a potência dissipada por esse receptor é de 30,0 V.
Resposta Questão 2
Letra B
O balanço de energia nos receptores nos informa que:
A equação mostrada acima pode ser reescrita em termos da tensão total e da força contraeletromotriz:
Logo, a potência dissipada pelo receptor deve ser igual a 3,0 W.
Resposta Questão 3
Letra E
Observe a equação a seguir. Com ela, podemos calcular o rendimento de um receptor por meio da razão entre a sua força contraeletromotriz e a tensão estabelecida em seus terminais:
Dessa forma, tomando os dados informados pelo enunciado do exercício, o rendimento desse receptor é de:
No cálculo acima, após fazermos a razão de E por U, multiplicamos o resultado por 100, a fim de transformá-lo em uma porcentagem, resultando em aproximadamente 72% de rendimento.
Resposta Questão 4
Letra C
A equação dos receptores nos informa que o potencial elétrico total fornecido a um receptor, em Volts (U), é igual ao potencial mínimo necessário para o seu funcionamento, a força contraeletromotriz (E), somada ao potencial elétrico dissipado em decorrência do efeito Joule (r.i), logo:
Tomando os dados fornecidos pelo enunciado do exercício teremos:
Portanto, esse receptor tem resistência interna de 4,0 Ω.