Questão 1
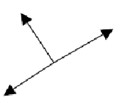
(PUC-MG) A figura 1 representa um bloco de massa m que, após ser lançado com velocidade v, sobe uma rampa de comprimento L, sem atrito, inclinada de um ângulo q.
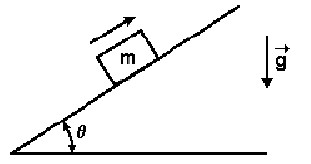
Assinale a opção que corresponde às forças que atuam no bloco enquanto ele estiver subindo a rampa.
a)
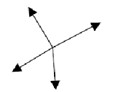
b)
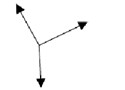
c)
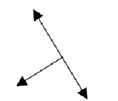
d)
Questão 2
(Unimep-SP) Um bloco de massa 5 kg é arrastado ao longo de um plano inclinado sem atrito, conforme a figura.
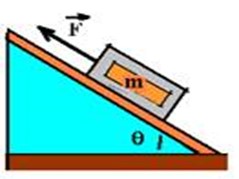
Para que o bloco adquira uma aceleração de \(3{m}/{s^2}\) para cima, a intensidade de \(\vec{F}\) deverá ser: \((g=10{m}/{s^2}, senq=0,8 \ e\ cosq=0,6)\):
a) igual ao peso do bloco
b) menor que o peso do bloco
c) igual à reação do plano
d) igual a 55 N
e) igual a 10 N
Questão 3
(Ufal - adaptada) Uma rampa AB, inclinada de 37° em relação à horizontal, tem 12 m de comprimento e não oferece atrito para um pequeno corpo de massa 1,0 kg, abandonado, a partir do repouso no ponto A.
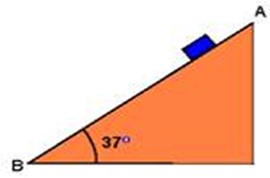
Adote \( g=10{m}/{s^2}\), cos 37° = 0,80 e sen 37° = 0,60. Determine a força resultante sobre o corpo.
a) 5 N
b) 6 N
c) 7 N
d) 8 N
e) 9 N
Questão 4
(Fatec-SP) Um fio, que tem suas extremidades presas aos corpos A e B, passa por uma roldana sem atrito e de massa desprezível. O corpo A, de massa 1,0 kg, está apoiado num plano inclinado de 37° com a horizontal, suposto sem atrito. Adote \(g=10{m}/{s^2}\) , sen 37° = 0,60 e cos 37° = 0,80.
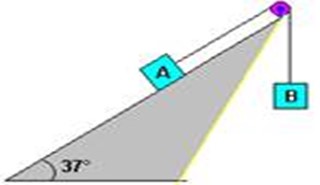
Para o corpo B descer com aceleração de \(2,0\ {m}/{s^2}\) , o seu peso deve ser, em Newtons,
a) 2,0
b) 6,0
c) 8,0
d) 10,0
e) 20,0
Questão 5
Uma pessoa está puxando por um fio uma caixa por um plano inclinado com atrito. Com base nessas informações, quais das forças abaixo não estão atuando nessa caixa?
a) força elástica.
b) força normal.
c) força de atrito.
d) força peso.
e) força de tração.
Questão 6
Em um plano inclinado de 30º com a horizontal é abandonado um bloco de 10 kg. Desconsiderando o atrito entre o plano e o bloco, calcule a aceleração desse bloco.
Adote 
\( g=10\ {m}/{s^2}\) , sen 30° = 0,5 e cos 30° = 0,9.
a) \(1{m}/{s^2}\)
b) \(2{m}/{s^2}\)
c) \(3{m}/{s^2}\)
d) \(4{m}/{s^2}\)
e) \(5{m}/{s^2}\)
Questão 7
Calcule o ângulo de inclinação de um plano inclinado que possui um corpo apoiado sobre ele, considere que a força normal sobre o corpo é de 50 N e a força peso sobre ele é de 100 N.
a) 30°
b) 60°
c) 90°
d) 120°
e) 180°
Questão 8
O plano inclinado é um dos assuntos mais importantes estudados na Dinâmica, nele analisamos os corpos em dois casos de plano inclinado. Pensando nisso, qual das alternativas abaixo se trata desses casos de plano inclinado?
I - Plano inclinado com atrito.
II - Plano inclinado deformável.
III - Plano inclinado sem atrito.
IV - Plano inclinado resistente.
a) Alternativas I e II.
b) Alternativas III e IV.
c) Alternativas I e III.
d) Alternativas II e IV.
e) Alternativas I e IV.
Questão 9
Determine a força mínima que deve ser aplicada sobre um bloco de 4,5 kg para que ele se mova com velocidade constante na superfície de um plano inclinado sem atrito com ângulo de inclinação de 60º.
Adote \(g=10{m}/{s^2}, \), sen 60° = 0,9 e cos 60° = 0,5.
a) 40,5 N
b) 52,1 N
c) 68,4 N
d) 71,3 N
e) 85,2 N
Questão 10
Um guindaste puxa um carro por meio de um fio em um piso inclinado sem atrito. Responda: quais das forças abaixo não estão atuando sobre esse carro?
a) força peso.
b) força normal.
c) força de atrito.
d) força de resistência do ar.
e) força de tração.
Questão 11
Determine a força de atrito sobre um corpo de 15 kg que se move em um plano inclinado de 20º com a horizontal.
Adote \(g=10{m}/{s^2}\), \(\mu_c=0,4\) , sen 20° = 0,3 e cos 20° = 0,9.
a) 12 N
b) 14 N
c) 16 N
d) 18 N
e) 20 N
Questão 12
Quais das alternativas apresentam a unidade de medida correspondente às grandezas físicas estudadas no plano inclinado?
- A força de atrito é medida em Joule.
- A força normal é medida em Newton.
- A força peso é medida em Newton por Joule.
- A massa é medida em quilogramas.
- A aceleração da gravidade é medida em metros por segundo.
a) Alternativas I e II.
b) Alternativas III e IV.
c) Alternativas I e V.
d) Alternativas II e III.
e) Alternativas II e IV.
Resposta Questão 1
LETRA C
Temos a força normal perpendicular à superfície e a força peso apontando para o centro da Terra, que foi decomposta em suas duas componentes, uma perpendicular ao bloco para a esquerda e outra perpendicular ao bloco para baixo.
Resposta Questão 2
LETRA D
As forças atuantes nesse bloco são a força peso, a força normal e a força \(\vec{F}\). Decompondo a força peso em suas componentes x e y é possível observar que a \(\ \vec{P_y}\) é igual a \(\vec{N}\), não sendo nenhuma delas responsável pelo movimento, então a força resultante será:
\(F_R=m\cdot a\)
\(F-P_x=m\cdot a\)
\(F-\left(P\cdot s e n\theta\right)=m\cdot a\)
\(F-\left(m\cdot g\cdot s e n\theta\right)=m\cdot a\)
\(F-\left(5\cdot10\cdot0,8\right)=5\cdot3\)
\(F-40=15\)
\(F=15+40\)
\(F=55\ N\)
Resposta Questão 3
LETRA B
As forças atuantes nesse bloco são a força peso e a força normal. Decompondo a força peso em suas componentes x e y é possível observar que \(a\vec{{P\ }_y}\) é igual a \( \vec{N} \) e \(\vec{P_x} \) é a única força atuando na horizontal, sendo ela a única responsável pelo movimento. Então, através da fórmula da força resultante, calcularemos a aceleração desse bloco:
\(F_R=m\cdot a\)
\(P_x=m\cdot a\)
\(P\cdot sen37°=m\cdot a\)
\(m\cdot g\cdot sen37°=m\cdot a\)
\(1\cdot10\cdot0,6=1\cdot a\)
\(6=1\cdot a\)
\(a=6\ {m}/{s^2}\)
Então a força resultante será:
\(F_R=m\cdot a\)
\(F_R=1\cdot6\)
\(F_R=6\ N\)
Resposta Questão 4
LETRA D
Para calcularemos a força peso sobre o bloco B, é necessário analisarmos as forças atuantes em cada bloco. No bloco A temos a força tração, força peso e força normal e no bloco B temos a força tração e a força peso.
Então, calcularemos a força tração através da fórmula da força resultante no bloco A. Como o bloco B desce, no bloco A a força tração será maior que a componente x da força peso, então:
\(F_R=m\cdot a\)
\(T-P_x=m\cdot a\)
\(T-(P\cdot sen 37°)=m\cdot a\)
\(T-(m\cdot g\cdot sen 37°)=m\cdot a\)
\(T-\left(1\cdot10\cdot0,6\right)=1\cdot2\)
\(T-6=2\)
\(T=2+6\)
\(T=8\ N\)
Como o bloco B está descendo, a sua força peso é maior que a força tração, então:
\(F_R=m\cdot a\)
\(P-T=m\cdot a\)
\(P-8=1\cdot2\)
\(P-8=2\)
\(P=2+8\)
\(P=10\ N\)
Resposta Questão 5
LETRA A
Nessa situação não foi mencionada a atuação de nenhum material com capacidade de deformar, como molas, por isso não temos a força elástica atuando sobre essa caixa.
Resposta Questão 6
LETRA E
As forças atuantes nesse bloco são a força peso e a força normal, então decompondo a força peso em suas componentes x e y é possível observar que a \(\vec{P_y} \) é igual a \( \vec{N}\) e \(\vec{P_x}\) é a única força atuando na horizontal, sendo ela a única responsável pelo movimento. Então através da fórmula da força resultante calcularemos a aceleração desse bloco:
\(F_R=m\cdot a\)
\(P_x=m\cdot a\)
\(P\cdot sen\ 30°=m\cdot a\)
\(m\cdot g\cdot sen\ 30°=m\cdot a\)
\(10\cdot10\cdot0,5=10\cdot a\)
\(50=10\cdot a\)
\(a=5{m}/{s^2}\)
Resposta Questão 7
LETRA B
Calcularemos o ângulo de inclinado do plano através da fórmula que o relaciona à força normal e força peso:
\(N=P\cdot cos\theta\)
\(\frac{50}{100}=cos\theta\)
\(0,5=cos\theta\)
\(60°=θ\)
Resposta Questão 8
LETRA C
Os tipos de plano inclinado são plano inclinado com atrito, em que levamos em consideração a força de atrito atuando sobre os corpos, e plano inclinado sem atrito, em que desconsideramos a força de atrito atuando sobre os corpos.
Resposta Questão 9
LETRA A
Para o bloco se mover com velocidade constante é necessário que a força resultante atuando sobre ele seja nula, portanto a força mínima precisa ser igual à componente x da força peso para que elas se cancelem:
\(F_R=P_x\)
\(F_R=P\cdot sen\theta\)
\(F_R=m\cdot g\cdot sen\ 60°\)
\(F_R=4,5\cdot10\cdot0,9\)
\(F_R=40,5\ N\)
Resposta Questão 10
LETRA C
Nessa situação foi mencionado que o piso não tem atrito, portanto não há força de atrito entre o carro e o piso.
Resposta Questão 11
LETRA D
As forças atuantes nesse bloco são a força peso, força normal e força de atrito. Então decompondo a força peso em suas componentes x e y é possível observar que a \(\vec{{\ P}_y}\) é igual a \( \vec{N}\)e \( \vec{P_x}\) e a \(\vec{f_{at}}\) são as forças atuando horizontal, sendo elas responsáveis pelo movimento.
Primeiramente, é necessário calcularmos a força normal \(\vec{N}\) , através da sua igualdade com a componente y da força peso \(\vec{P_y}\) :
\(\vec{N}=\vec{P_y}\)
\(\vec{N}=\vec{P_y}\)
\(\vec{N}=P\cdot sen\theta\)
\(\vec{N}=m\cdot g\cdot sen20°\)
\(\vec{N}=15\cdot10\cdot0,3\)
\(\vec{N}=45\ N\)
Por fim, calcularemos a força de atrito \( \vec{f_{at}}\) :
\(\vec{f_{at}}=\mu\cdot\vec{N}\)
\(\vec{f_{at}}=0,4\cdot45\)
\(\vec{f_{at}}=18\ N\)
Resposta Questão 12
LETRA E
Apenas as alternativas II e IV estão corretas. Abaixo, em vermelho, vemos a correção das outras alternativas.
- Incorreta. A força de atrito é medida em Joule.
- Correta.
- Incorreta. A força peso é medida em Newton.
- Correta.
- Incorreta. A aceleração da gravidade é medida em metros por segundo ao quadrado.