Questão 1
Questão 1
(UFPel) Um caminhão-tanque, após sair do posto, segue, com velocidade constante, por uma rua plana que, num dado trecho, é plana e inclinada.
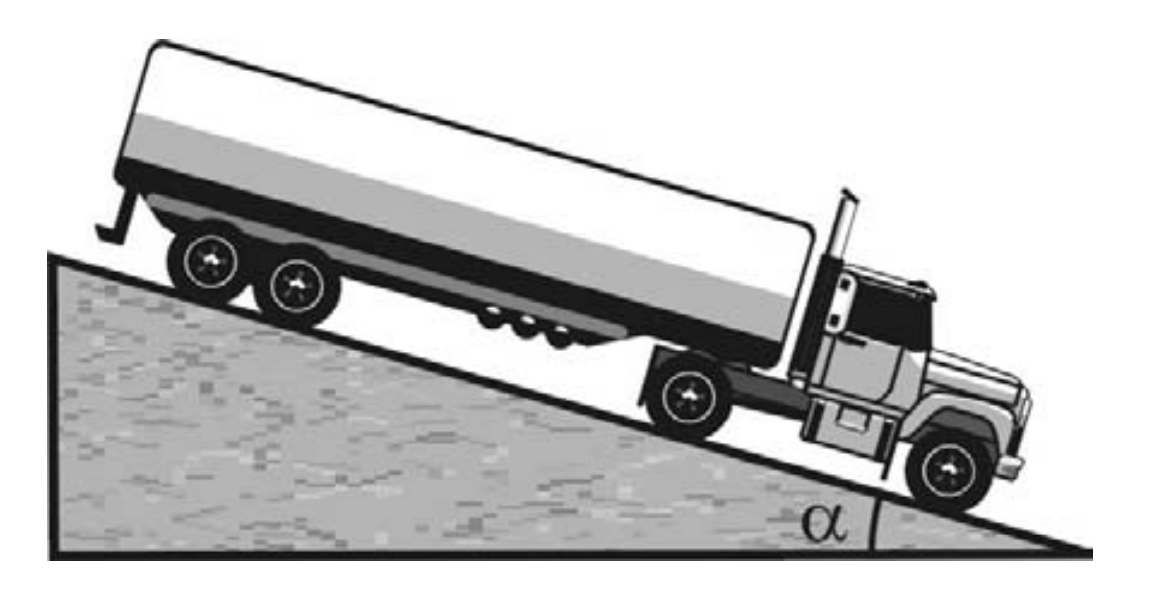
O módulo da aceleração da gravidade, no local, é g = 10 m/s2
, e a massa do caminhão, 22t, sem considerar a do combustível. É correto afirmar que o coeficiente de atrito dinâmico entre o caminhão e a rua é
A) μ = cot α
B) μ = csc α
C) μ = sen α
D) μ = tg α
E) μ = cos α
Questão 2
(PUC) Os corpos A e B de massas mA e mB, respectivamente, estão interligados por um fio que passa pela polia, conforme a figura. A polia pode girar livremente em torno de seu eixo. As massas do fio e da polia são desprezíveis.
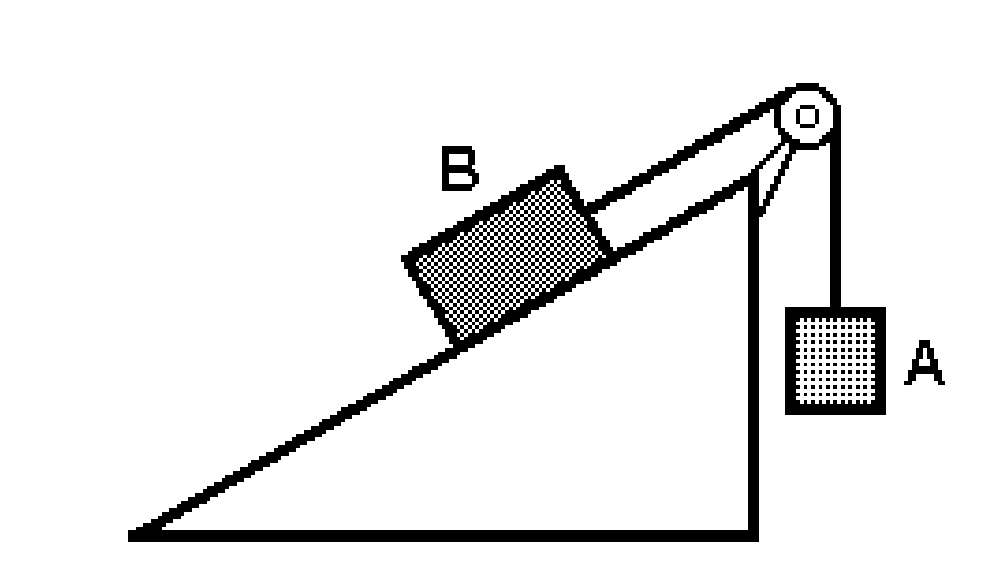
Se o sistema está em repouso, é correto afirmar:
I. Se mA = mB, necessariamente existe atrito entre o corpo B e o plano inclinado.
II. Independente de existir ou não atrito entre o plano e o corpo B, deve-se ter mA = mB.
III. Se não existir atrito entre o corpo B e o plano inclinado, necessariamente mA > mB.
IV. Se não existir atrito entre o corpo B e o plano inclinado, necessariamente mB > mA.
Está correta ou estão corretas:
A) Somente I
B) Somente II
C) I e III
D) I e IV
E) Somente III
Questão 3
(Mackenzie) A ilustração refere-se a certa tarefa na qual o bloco B, dez vezes mais pesado que o bloco A, deverá descer pelo plano inclinado com velocidade constante.
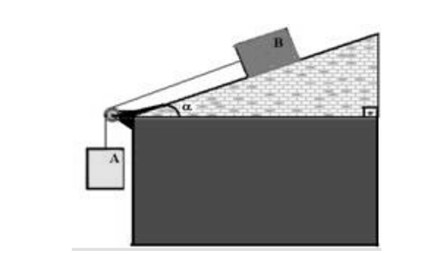
Considerando que o fio e a polia são ideais, o coeficiente de atrito cinético entre o bloco B e o plano deverá ser:
(Dados: senα = 0,6 e cosα = 0,8)
A) 1,50
B) 1,33
C) 0,875
D) 0,750
E) 0,500
Questão 4
(Unesp - Adaptada) Ao modificar o estilo de uma casa para o colonial, deseja-se fazer a troca do modelo de telhas existentes. Com o intuito de preservar o jardim, foi montada uma rampa de 10 m de comprimento, apoiada na beirada do madeiramento do telhado, a 6 m de altura. No momento em que uma telha — que tem massa de 2,5 kg — é colocada sobre a rampa, ela desce acelerada, sofrendo, no entanto, a ação do atrito. Nessas condições, determine o valor da aceleração desenvolvida pela telha. Dado: coeficiente de atrito \(\mu\)=0,2
; g = 10 m/s2
.
A) 4,4 m/s2
B) 6,6 m/s2
C) 8,8 m/s2
D) 12,2 m/s2
E) 14,0 m/s2
Questão 5
Em um plano inclinado de 45º com a horizontal, é abandonado um bloco de 30 kg. Considerando o atrito entre o plano e o bloco, calcule a aceleração desse bloco.
Adote g=10 m/s2 , sen 45° = cos 45° = 0,7.
A) 0,8 m/s2
B) 1,0 m/s2
C) 1,2 m/s2
D) 1,4 m/s2
E) 1,6 m/s2
Questão 6
Um carro puxa uma skatista por um fio em uma rua com coeficiente de atrito igual a 0,5. Pensando nisso, qual das forças abaixo não está atuando nessa situação.
A) Força peso
B) Força elástica
C) Força normal
D) Força de atrito
E) Força de tração
Questão 7
Calcule o ângulo de inclinação aproximado de um plano inclinado com atrito que tem um corpo apoiado sobre ele. Considere que a força normal sobre o corpo é de 200 N e a força peso sobre ele é de 650 N.
A) 5,47°
B) 8,96°
C) 11,84°
D) 17,92°
E) 28,88°
Questão 8
O plano inclinado com atrito é um dos assuntos mais importantes estudados na dinâmica, ele se diferencia do outro caso de plano inclinado devido à presença de qual força?
A) Força elástica
B) Força peso
C) Força de tração
D) Força normal
E) Força de atrito
Questão 9
Determine o coeficiente de atrito cinético sobre um corpo de 5 kg, que se desloca em um plano inclinado, com atrito de 60º com a horizontal, que sofre a ação de uma força de atrito de 22,5 N. Adote g = 10 m/s2 , \(\mu_c = 0,7
\), sen 60° = 0,9 e cos 60° = 0,5.
A) 0,4
B) 0,5
C) 0,6
D) 0,7
E) 0,8
Questão 10
Determine qual das forças abaixo não está atuando em um bloco que está sendo empurrado por uma pessoa em um plano inclinado com atrito:
A) Força da pessoa
B) Força de atrito
C) Força de tração
D) Força peso
E) Força normal
Questão 11
Determine a força de atrito sobre um corpo de 50 kg que se desloca em um plano inclinado de 30º com a horizontal. Adote g=10 m/s2 , \(\mu_c = 0,7
\), sen 30° = 0,5 e cos 30° = 0,9.
A) 175 N
B) 200 N
C) 225 N
D) 250 N
E) 275 N
Questão 12
Quais das alternativas abaixo apresentam a unidade de medida correspondente às grandezas físicas estudadas no plano inclinado com atrito?
I. A força de atrito é medida em Joule-Newton.
II. A força normal é medida em Newton.
III. A força peso é medida em Newton.
IV. A massa é medida em quilograma-metro.
V. A aceleração da gravidade é medida em metros por segundo.
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I e V.
D) Alternativas II e III.
E) Alternativas II e IV.
Resposta Questão 1
Alternativa D
Calcularemos o coeficiente de atrito dinâmico pela fórmula da força de atrito:
\(\vec{f_{\text{at}}} = \mu \cdot \vec{N} \)
Em que, isolando o coeficiente de atrito dinâmico, temos:
\(\mu = \frac{\vec{f_{\text{at}}}}{\vec{N}} \)
Em que a força de atrito é igual à componente x da força peso e a força normal é igual à componente y da força peso:
\(\mu = \frac{\vec{P_x}}{\vec{P_y}} \)
\( \mu = \frac{P \cdot sen \ {\theta}}{P \cdot \cos{\theta}} \)
\( \mu = \frac{sen\ {\theta}}{\cos{\theta}} \)
\(\mu = tg \ {\theta}\)
Resposta Questão 2
Alternativa D
I. Se mA = mB, necessariamente existe atrito entre o corpo B e o plano inclinado. (correta)
II. Independente de existir ou não atrito entre o plano e o corpo B, deve-se ter mA = mB. (incorreta)
Se as massas são iguais, é necessário existir atrito entre o bloco B e a superfície.
III. Se não existir atrito entre o corpo B e o plano inclinado, necessariamente mA > mB. (incorreta)
Se não existir atrito entre o corpo B e o plano inclinado, necessariamente mA > mB.
IV. Se não existir atrito entre o corpo B e o plano inclinado, necessariamente mB > mA. (correta)
Resposta Questão 3
Alternativa C
Como a velocidade é constante, a aceleração dos blocos é nula. As forças atuantes no bloco A são a força peso e a força de tração, sendo responsáveis pelo movimento. Então calcularemos a força de tração, igualando-a à força peso sobre A:
\(P_A = T \)
\(m_A \cdot g = T \)
\(m_A \cdot 10 = T \)
\(10 \cdot m_A = T \)
Já no bloco B, as forças atuantes sobre ele são a força peso, a força normal, a força de tração e a força de atrito, então, decompondo a força peso em suas componentes x e y, é possível observar que a Py é igual à força normal N , e a força de tração com a Px são iguais à força de atrito fat
, se\ndo essas três as responsáveis pelo movimento horizontal.
Depois, calcularemos a força Normal N pela sua equivalência com a componente y da força peso Py
:
\(\vec{N} = \vec{P_By} \)
\(\vec{N} = P \cdot \cos{\alpha} \)
\(\vec{N} = m_B \cdot 10 \cdot 0,8 \)
\(\vec{N} = 8\ m_B \)
Como a massa do bloco B é 10 vezes a massa do bloco A, temos:
\(\vec{N}= 8 \cdot 10 \,m_A \)
\(\vec{N} = 80 \, m_A \)
Por fim, calcularemos o coeficiente de atrito cinético por meio da fórmula da força de atrito:
\(\vec{f_{\text{at}}} = T + \vec{P_{Bx}} \)
\(\mu \cdot \vec{N} = T + P_B \cdot sen\ {\alpha} \)
\(\mu \cdot 80 \, m_A = 10 \, m_A + m_B \cdot g \cdot 0,6 \)
\(\mu \cdot 80 \, m_A = 10 \, m_A + m_B \cdot 10 \cdot 0,6 \)
\(\mu \cdot 80 \, m_A = 10 \, m_A + 10 \, m_A \cdot 6 \)
\(\mu \cdot 80 \, m_A = 10 \, m_A + 60 \, m_A \)
\(\mu \cdot 80 \, m_A = 10 \, m_A + 60 \, m_A \)
\(\mu \cdot 80 \, m_A = 70 \, m_A\)
\(\mu = \frac{70 \, \text{mA}}{80 \, \text{mA}} \)
\(\mu = 0,875 \)
Resposta Questão 4
Alternativa A
Primeiramente, calcularemos o tamanho da base do triângulo formado usando o teorema de Pitágoras:
\(\text{hipotenusa}^2 = \text{cateto}^2 + \text{cateto}^2\)
\(10^2 = 6^2 + \text{cateto}^2\)
\(100 - 36 = \text{cateto}^2\)
\(64 = \text{cateto}^2 \)
\(\sqrt{64} = \text{cateto}\)
\(8 \, \text{m} = \text{cateto}\)
Depois, calcularemos o seno e o cosseno do ângulo formado com a horizontal:
\(\text{sen}{\theta} = \frac{6}{10} = 0,6\)
\(\cos{\theta} = \frac{8}{10} = 0,8\)
As forças atuantes nesse bloco são a força peso, força normal e força de atrito, então, decompondo a força peso em suas componentes x e y, é possível observar que a (P_y ) ⃗ é igual à N ⃗, e (P_x ) ⃗ e (f_at ) ⃗ são as forças atuando na horizontal, sendo responsáveis pelo movimento. Então calcularemos a aceleração desse bloco, dada pela fórmula da segunda lei de Newton:
\(F_R = m \cdot a\)
\(\vec{P_x} - \vec{f_{\text{at}}} = m \cdot a \)
\(P \cdot \text{sen}{\theta} - \mu \cdot \vec{N} = m \cdot a\)
\(P \cdot \text{sen}{\theta} - \mu \cdot P \cdot \cos{\theta} = m \cdot a\)
\(P \cdot (\text{sen}{\theta} - \mu \cdot \cos{\theta}) = m \cdot a\)
\(m \cdot g \cdot (\text{sen}{\theta} - \mu \cdot \cos{\theta}) = m \cdot a\)
\(g \cdot (\text{sen}{\theta} - \mu \cdot \cos{\theta}) = a\)
\(10 \cdot (0,6 - 0,2 \cdot 0,8) = a\)
\(10 \cdot (0,6 - 0,16) = a\)
\(10 \cdot (0,44) = a \)
\(4,4 \, \text{m/s}^2 = a\)
Resposta Questão 5
Alternativa C
As forças atuantes nesse bloco são a força peso, força normal e força de atrito, então, decompondo a força peso em suas componentes x e y, é possível observar que a \(\vec{P_y} \) é igual à \(\vec{N} \) , e \(\vec{P_x} \) e \(\vec{f_{at}} \)
são as forças atuando horizontal, sendo responsáveis pelo movimento.
Primeiramente, calcularemos a força normal \(\vec{N} \) por meio da sua equivalência com a componente y da força peso \(\vec{P_y} \) :
\(\vec{N} = \vec{P_y} \)
\(\vec{N} = P \cdot \cos{\theta} \)
\(\vec{N} = m \cdot g \cdot \cos{45^\circ} \)
\(\vec{N} = 30 \cdot 10 \cdot 0,7 \)
\(\vec{N} = 210 \, \text{N} \)
Depois, calcularemos a força de atrito fat por meio da sua fórmula:
\(\vec{f_{\text{at}}} = \mu \cdot \vec{N} \)
\(\vec{f_{\text{at}}} = 0,7 \cdot 250 \)
\(\vec{f_{\text{at}}} = 175 \, \text{N} \)
Então, calcularemos a aceleração desse bloco, dada pela fórmula da segunda lei de Newton:
\(F_R = m \cdot a \)
\(\vec{P_x} - \vec{f_{\text{at}}} = m \cdot a \)
\(P \cdot \text{sen}{45^\circ} - \vec{f_{\text{at}}} = m \cdot a \)
\(m \cdot g \cdot \text{sen}{45^\circ} - \vec{f_{\text{at}}} = m \cdot a \)
\(30 \cdot 10 \cdot 0,7 - 175 = 30 \cdot a \)
\(210 - 175 = 30 \cdot a \)
\(35 = 30 \cdot a \)
\(a = \frac{35}{30} \)
\(a \approx 1,2 \, \text{m/s}^2 \)
Resposta Questão 6
Alternativa B
Nessa situação, não temos a presença de molas ou materiais deformáveis, em razão disso, não temos a atuação da força elástica.
Resposta Questão 7
Alternativa D
Calcularemos o ângulo de inclinado do plano inclinado com atrito pela fórmula que o relaciona à força normal e à força peso:
\(N = P_y\)
\(N = P \cdot \cos{\theta} \)
\(\frac{200}{650} = \cos{\theta} \)
\(0,307 \approx \cos{\theta} \)
\(17,92^\circ \approx \theta\)
Resposta Questão 8
Alternativa E
Os tipos de plano inclinado são plano inclinado com atrito e plano inclinado sem atrito, que se diferenciam quando da análise das forças em um bloco considerando-se ou não a presença da força de atrito respectivamente.
Resposta Questão 9
Alternativa B
As forças atuantes nesse bloco são a força peso, força normal e força de atrito, então, decompondo a força peso em suas componentes x e y, é possível observar que a \( \vec{P_y}
\) é igual à \(\vec{N}\) , e \(\vec{P_x}
\) e a \(\vec{f_{at}}\) são as forças atuando horizontal, sendo responsáveis pelo movimento.
Primeiramente, calcularemos a força normal \(\vec{N}\) por meio da sua equivalência com a componente y da força peso \( \vec{P_y}
\):
\(\vec{N} = \vec{P_y}
\)
\(\vec{N} = P \cdot \text{sen}{\theta} \)
\(\vec{N} = m \cdot g \cdot \text{sen}{60^\circ} \)
\(\vec{N} = 5 \cdot 10 \cdot 0,9 \)
\(\vec{N} = 45 \, \text{N} \)
Por fim, calcula-se o coeficiente de atrito cinético por meio da fórmula da força de atrito:
\(\vec{f_{\text{at}}} = \mu \cdot \vec{N} \)
\(22,5 = \mu \cdot 45 \)
\(\mu = \frac{22,5}{45} \)
\(\mu = 0,5 \)
Resposta Questão 10
Alternativa C
Nessa situação, não temos a força de tração, já que não há atuação de nenhum fio sobre o bloco.
Resposta Questão 11
Alternativa A
As forças atuantes nesse bloco são a força peso, força normal e força de atrito, então, decompondo a força peso em suas componentes x e y, é possível observar que a \(\vec{P_y}
\) é igual à \(\vec{N}\), e \(\vec{P_x}
\) e \(\vec{f_{at}}
\) são as forças atuando horizontal, sendo responsáveis pelo movimento.
Primeiramente, calcularemos a força normal \(\vec{N}\) por meio da sua equivalência com a componente y da força peso \(\vec{P_y} \):
\(\vec{N} = \vec{P_y} \)
\(\vec{N} = P \cdot \text{sen}{\theta} \)
\(\vec{N} = m \cdot g \cdot \text{sen}{30^\circ} \)
\(\vec{N} = 50 \cdot 10 \cdot 0,5 \)
\(\vec{N} = 250 \, \text{N} \)
Por fim, calcularemos a força de atrito \(\vec{f_{at}} \) por meio da sua fórmula:
\(\vec{f_{\text{at}}} = \mu \cdot \vec{N} \)
\(\vec{f_{\text{at}}} = 0,7 \cdot 250 \)
\(\vec{f_{\text{at}}} = 175 \, \text{N} \)
Resposta Questão 12
Alternativa D
I. A força de atrito é medida em Joule-Newton. (incorreta)
A força de atrito é medida em Newton.
II. A força normal é medida em Newton. (correta)
III. A força peso é medida em Newton. (correta)
IV. A massa é medida em quilograma-metro. (incorreta)
A massa é medida em quilograma.
V. A aceleração da gravidade é medida em metros por segundo. (incorreta)
A aceleração da gravidade é medida em metros por segundo ao quadrado.
