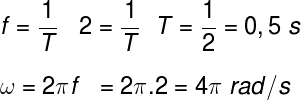Questão 1
(UEFS) A figura representa um sistema massa-mola ideal, cuja constante elástica é de 4 N/cm.
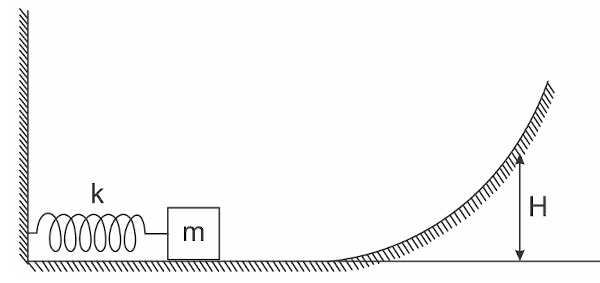
Um corpo de massa igual a 1,2 kg é empurrado contra a mola, comprimindo-a de 12,0 cm. Ao ser liberado, o corpo desliza ao longo da trajetória representada na figura. Desprezando-se as forças dissipativas em todo o percurso e considerando a aceleração da gravidade igual a 10 m/s², é correto afirmar que a altura máxima H atingida pelo corpo, em cm, é igual a:
a) 24
b) 26
c) 28
d) 30
e) 32
Questão 2
(Aman) Uma mola ideal está suspensa verticalmente, presa a um ponto fixo no teto de uma sala por uma de suas extremidades. Um corpo de massa 80 g é preso à extremidade livre da mola e verifica-se que a mola desloca-se para uma nova posição de equilíbrio. O corpo é puxado verticalmente para baixo e abandonado de modo que o sistema massa-mola passa a executar um movimento harmônico simples. Desprezando as forças dissipativas, sabendo que a constante elástica da mola vale 0,5 N/m e considerando π = 3,14, o período do movimento executado pelo corpo é de:
a) 1,256 s
b) 2,512 s
c) 6,369 s
d) 7,850 s
e) 15,700 s
Questão 3
Determine a frequência angular de um oscilador massa-mola de constante elástica igual a 640 N/m, presa a um corpo de massa igual a 10 kg.
a) 0,05 rad/s
b) 20 rad/s
c) 10 rad/s
d) 5 rad/s
e) 8 rad/s
Questão 4
Um sistema massa-mola ideal oscila com frequência de 2 Hz. O período e a frequência angular desse oscilador, em unidades SI, são, respectivamente:
a) 2,5 s e 4 rad/s
b) 0,4 s e 5π rad/s
c) 0,5 s e 4π rad/s
d) 1,0 s e 2π rad/s
e) 8,0 s e 5π rad/s
Resposta Questão 1
Letra A. Primeiramente, é necessário perceber que toda a energia potencial elástica transforma-se em energia potencial gravitacional no ponto mais alto que o objeto de massa m é capaz de alcançar. Além disso, é necessário adequar as unidades: a constante elástica – vale 4 N/cm, logo 400 N/m – e a deformação da mola (0,12 m). Fazendo isso, basta resolver o seguinte cálculo:
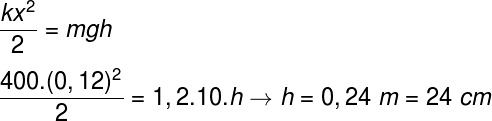
Resposta Questão 2
Letra B. Para resolvermos o exercício, é preciso lembrar as relações entre a frequência angular, período, massa e constante elástica, mostradas na fórmula a seguir:
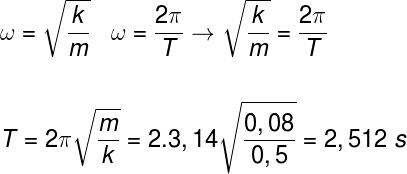
De acordo com o cálculo, o período desse movimento é igual a 2,512 s.
Resposta Questão 3
Letra C. A resolução do exercício requer que se calcule a frequência angular. Essa grandeza pode ser calculada por meio da raiz quadrada da razão entre a constante elástica e a massa.
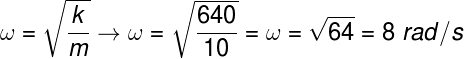
Resposta Questão 4
Letra C. Vamos calcular a frequência e o período desse sistema massa-mola: