Questão 1
(Unifesp) Duas partículas de cargas elétricas \(Q_1=4,0\cdot{10}^{-16}C\) e \(Q_2=6,0\cdot{10}^{-16}\ C\) estão separadas no vácuo por uma distância de \(3,0\cdot{10}^{-9\ }m\). Sendo \(k_o=9\ \cdot{10}^{9\ }N{\ m}^2\ /C^2\) , a intensidade da força de interação entre elas, em Newtons, é de:
a) \(1,2\cdot{10}^{-5\ }\)
b) \(1,8\cdot{10}^{-4\ }\)
c) \(2,0\cdot{10}^{-4\ }\)
d) \(2,4\cdot{10}^{-4\ }\)
e) \(3,0\cdot{10}^{-3\ }\)
Questão 2
(PUC-Rio) Dois objetos metálicos esféricos idênticos, contendo cargas elétricas de 1C e de 5C, são colocados em contato e depois afastados a uma distância de 3 m. Considerando a constante de Coulomb \(k_o=\ 9\ \cdot{10}^9\ N{\ m}^2\ /C^2\) , podemos dizer que a força que atua entre as cargas após o contato é:
a) atrativa e tem módulo 3∙109N .
b) atrativa e tem módulo 9∙109N .
c) repulsiva e tem módulo 3∙109N .
d) repulsiva e tem módulo 9∙109N .
e) zero
Questão 3
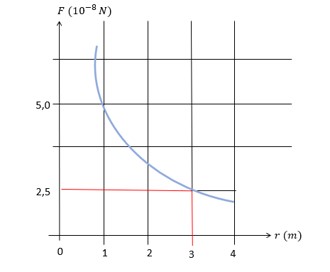
(UFPE) O gráfico a seguir representa a força F entre duas cargas puntiformes positivas de mesmo valor, separadas pela distância r. Considere \(k_o=9\ \cdot{10}^9\ N{\ m}^2\ /C^2\) e determine o valor das cargas, em unidades de 10-9C .
a) 1,0
b) 2,0
c) 3,0
d) 4,0
e) 5,0
Questão 4
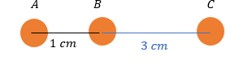
(Fuvest) Três objetos com cargas elétricas idênticas estão alinhados como mostra a figura. O objeto C exerce sobre B uma força igual a 3,0 ∙10-6 N. A força elétrica resultante dos efeitos de A e C sobre B é:
a) 2,0.10-6 N
b) 6,0.10-6 N
c) 12.10-6 N
d) 24.10-6 N
e) 30.10-6 N
Questão 5
Qual é a distância aproximada entre duas cargas elétricas iguais de 25 ∙10-6 C , se se atraem no vácuo com uma força de 100 N ?
a) 10 m
b) 0,24 m
c) 30 m
d) 5 m
e) 0,39 m
Questão 6
Determine a força elétrica entre duas cargas elétricas de valor Q1= 4μC e Q2= -3μC , distanciadas a 2 cm. Além disso, a força elétrica entre elas é repulsiva ou atrativa?
a) 270 N, atrativa
b) 8,0 N, repulsiva
c) 0 N, repulsiva
d) 80 N, atrativa
e) 2,7 N, atrativa
Questão 7
Duas cargas elétricas, uma q e outra Q , que possui o triplo de q , estavam inicialmente a uma distância d e foram aproximadas à metade da distância inicial. Com base nessas informações, a força elétrica final será de quanto da força inicial?
a) \(F_{final}=\frac{F_{inicial}}{8}\)
b) \(F_{final}={8\cdot F}_{inicial}\)
c) \(F_{final}=\frac{F_{inicial}}{4}\)
d) \(F_{final}=F_{inicial}\)
e) \(F_{final}={4\cdot F}_{inicial}\)
Questão 8
Duas cargas iguais com valor Q apresentam uma força repulsiva de 200 N e estão distanciadas a 80 cm uma da outra. Sabendo que \( k_o=\ 9\ \cdot{10}^9\ N{\ m}^2\ /C^2\), encontre o valor da carga Q.
a) +1,192∙10-4C e -1,192∙10-4 C
b) +1,192∙10-4C ou -1,192∙10-4 C
c) +1,192∙10-5C ou -1,192∙10-5 C
d) +1,192∙10-4 C
e) -1,192∙10-4 C
Questão 9
Comparando a distância inicial com a distância final, quando multiplicamos uma força elétrica final em nove vezes a força elétrica inicial de duas cargas q,
a) as distâncias são iguais.
b) a distâncial inicial é quatro vezes a distâncial final.
c) a distâncial final é três vezes a distâncial inicial.
d) a distâncial final é o dobro da distâncial inicial.
e) a distâncial inicial é metade da distâncial final.
Questão 10
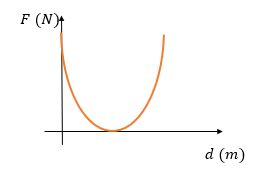
Entre os gráficos abaixo, qual deles expressa corretamente a lei de Coulomb?
a)
b)
c)
d)
e)
Questão 11
Após seus estudos a respeito da lei de Coulomb, qual alternativa abaixo corresponde à sua fórmula:
a) \(F=k\cdot\frac{\left|Q_1\right|\ \cdot\left|Q_2\right|}{d^2}\)
b) \(E=k\cdot\frac{\left|Q\right|}{d^2}\)
c) \(E_P=k\frac{\left|Q\right|\ \cdot\left|q\right|}{d}\)
d) \(E_P=q\cdot V\)
e) \(F=\left|q\right|\cdot E\)
Questão 12
Analise as alternativas abaixo referentes às unidades de medida estudadas na lei de Coulomb:
I. A unidade de medida da carga elétrica é Coulomb.
II. A unidade de medida do campo elétrico é Newton.
III. A unidade de medida da força elétrica é o Joule.
IV. A unidade de medida da distância é o metro.
Está(ão) correta(s):
a) I, II
b) III, IV
c) I, IV
d) II, III
e) I, II e IV
Resposta Questão 1
Letra D. A intensidade da força elétrica é determinada pela fórmula da lei de Coulomb:
\(F=k\cdot\frac{\left|Q_1\right|\ \cdot\left|Q_2\right|}{d^2}\)
\(F=9\ \cdot{10}^{9\ }\cdot\frac{\left|4,0\cdot{10}^{-16}\right|\ \cdot\left|6,0\cdot{10}^{-16}\right|}{{(3,0\cdot{10}^{-9\ })}^2}\)
\(F=9\ \cdot{10}^{9\ }\cdot\frac{4,0\cdot{10}^{-16}\ \cdot6,0\cdot{10}^{-16}}{9,0\cdot{10}^{-18\ }}\)
\(F=\frac{9\ \cdot4,0\cdot6,0\cdot{10}^{9\ }\cdot{10}^{-16}\cdot{10}^{-16}}{9,0\cdot{10}^{-18\ }}\)
\(F=24\cdot{10}^{9-16-16+18\ }\)
\(F=24\cdot{10}^{-5\ }\)
\(F=2,4\cdot{10}^{-4\ }\ N\)
Resposta Questão 2
Letra D. Analisando as cargas elétricas, vemos que, como elas estão em contato, ocorre uma troca de elétrons entre elas que só será finalizada quando ambas obtiverem o mesmo valor de carga elétrica. Para descobrir esse valor, calcularemos a média aritmética entre as cargas:
\(\frac{5+1}{2}=\frac{6}{2}=3\ C\)
Calcularemos agora a força elétrica por meio da lei de Coulomb:
\(F=k\frac{\left|Q_1\right|\ \cdot\left|Q_2\right|}{d^2}\)
\(F=9\cdot{10}^9\cdot\frac{\left|3\right|\cdot\left|3\right|}{3^2}\)
\(F=9\cdot{10}^9\cdot\frac{9}{9}\)
\(F=9\cdot{10}^9N\)
Resposta Questão 3
Letra E. Calcularemos o valor das cargas elétricas por meio da fórmula da lei de Coulomb:
\(F=k\frac{\left|Q_1\right|\ \cdot\left|Q_2\right|}{d^2}\)
De acordo com o gráfico, quando a força for F=2,5∙10-4 N e a distância for r=3 m, teremos um ponto em comum entre a curva e a reta, então substituiremos esses dados na fórmula:
\(2,5\cdot{10}^{-8}=9\ \cdot{10}^9\frac{\left|Q_1\right|\cdot\left|Q_2\right|}{3^2}\)
Como as cargas são iguais, podemos multiplicá-las:
\(2,5\cdot{10}^{-8}=9\ \cdot{10}^9\frac{Q^2}{3^2}\)
\(2,5\cdot{10}^{-8}=9\ \cdot{10}^9\frac{Q^2}{9}\)
\(2,5\cdot{10}^{-8}={10}^9{\cdot Q}^2\)
\(\frac{2,5\cdot{10}^{-8}}{{10}^9}=Q^2\)
\(2,5\cdot{10}^{-8-9}=Q^2\)
\(2,5\cdot{10}^{-17}=Q^2\)
\(25\cdot{10}^{-1}\cdot{10}^{-17}=Q^2\)
\(25\cdot{10}^{-1-17}=Q^2\)
\(25\cdot{10}^{-18}=Q^2\)
\(\sqrt{25\cdot{10}^{-18}}=Q\)
\(5\cdot{10}^{-9}C=Q\)
Resposta Questão 4
Letra D. Primeiramente, converteremos as dimensões de centímetros para metros:
\(1\ cm=1\cdot{10}^{-2}\ m\ \)
\(3\ cm=3\cdot{10}^{-2}\ m\ \)
Sabemos que força elétrica entre as partículas B e C é de 3,0∙10-6N , então substituiremos esse valor na fórmula da lei de Coulomb e calcularemos o valor da carga elétrica:
\(F_{CB}=k\cdot\frac{\left|Q_1\right|\ \cdot\left|Q_2\right|}{d^2}\)
\(3,0\cdot{10}^{-6}=9\cdot{10}^9\cdot\frac{\ \left|Q_1\right|\ \cdot\left|Q_2\right|}{\left(3\cdot{10}^{-2}\right)^2}\)
Como as cargas elétricas são iguais, basta multiplicá-las:
\(3,0\cdot{10}^{-6}=9\cdot{10}^9\cdot\frac{\ Q^2}{\left(3\cdot{10}^{-2}\right)^2}\)
\(3,0\cdot{10}^{-6}=9\cdot{10}^9\cdot\frac{\ Q^2}{9\cdot{10}^{-4}}\)
\(3,0\cdot{10}^{-6}={10}^{13}{\cdot Q}^2\)
\(3,0\cdot{10}^{-6}={10}^{13}{\cdot Q}^2\)
\(\frac{3,0\cdot{10}^{-6}}{{10}^{13}}=Q^2\)
\(3,0\cdot{10}^{-6-13}=Q^2\)
\(3,0\cdot{10}^{-19}C=Q^2\)
A força elétrica que a partícula A faz em B é:
\(F_{AB}=k\cdot\frac{\left|Q_1\right|\ \cdot\left|Q_2\right|}{d^2}\)
\(F_{AB}=k\cdot\frac{Q^2}{d^2}\)
\(F_{AB}=9\cdot{10}^9\cdot\frac{\ 3,0\cdot{10}^{-19}}{\left(1\cdot{10}^{-2}\right)^2}\)
\(F_{AB}=9\cdot{10}^9\cdot\frac{3,0\cdot{10}^{-19}}{1\cdot{10}^{-4}}\)
\(F_{AB}=9\cdot{10}^9\cdot3,0\cdot{10}^{-19+4}\)
\(F_{AB}=27\cdot{10}^9\cdot{10}^{-15}\)
\(F_{AB}=27\cdot{10}^{9-16}\)
\(F_{AB}=27\cdot{10}^{-6}N\)
A força resultante na partícula B pode ser obtida pelo somatório entre a força elétrica na partícula A com a força elétrica na partícula C. Contudo, como as partículas apresentam sentidos opostos, já que as cargas elétricas possuem o mesmo sinal, então a soma se torna uma subtração:
\(F_B=F_{AB}-F_{CB}\)
\(F_B=27,0\cdot{10}^{-6}-3,0\cdot{10}^{-6}\)
\(F_B=24,0\cdot{10}^{-6}\ N\ \)
Resposta Questão 5
Letra B. Usando a lei de Coulomb, conseguiremos determinar a distância entre as cargas elétricas:
\(F=k\frac{\left|Q_1\right|\ \cdot\left|Q_2\right|}{d^2}\)
Sabendo que a constante ko=9 ∙109 N m2 /C2 e que como as cargas se atraem, então elas possuem sinais opostos:
\(100=\ 9\ \cdot{10}^{9\ }\cdot\frac{\left|25\cdot{10}^{-6}\right|\ \cdot\left|-25\cdot{10}^{-6}\right|}{d^2}\)
\(100=\ 9\ \cdot{10}^{9\ }\cdot\frac{\left|25\cdot{10}^{-6}\right|\ \cdot\left|25\cdot{10}^{-6}\right|}{d^2}\)
\(100\cdot d^2=\ 9\ \cdot25\cdot25\cdot{{10}^{9\ }\cdot10}^{-6}\ \cdot{10}^{-6}\)
\(100\cdot d^2=\ 5625\cdot{10}^{9-6-6}\)
\(100\cdot d^2=\ 5625\ \cdot{10}^{-3}\ \)
\(d^2=\frac{5625\ \cdot{10}^{-3}}{100}\)
\(d^2=\frac{5625\ \cdot{10}^{-3}}{100}\)
\(d^2=56,25\ \cdot{10}^{-3}\)
\(d^2=5,625\cdot{10}^1\ \cdot{10}^{-3}\)
\(d^2=5,625\cdot{10}^{1-3}\)
\(d^2=5,625\cdot{10}^{-2}\)
\(d=\sqrt{5,625\cdot{10}^{-2}}\ \)
\(d=\sqrt{0,05625}\ \)
\(d\approx0,24\ m\ \)
Resposta Questão 6
Letra A. Primeiramente, converteremos a distância de centímetros para metros:
\(2\ cm=0,02\ metros\)
Calcularemos a força elétrica por meio da fórmula da lei de Coulomb:
\(F=k\frac{\left|Q_1\right|\cdot\left|Q_2\right|}{d^2}\)
Sabendo que a constante \(k_o=9\ \cdot{10}^9\ N{\ m}^2\ /C^2\) :
\(F=9\ \cdot{10}^{9\ }\frac{\left|4\mu C\right|\ \cdot\left|-3\mu C\right|}{{(0,02\ )}^2}\)
Substituiremos no lugar do símbolo micro (μ) o seu valor de 10-6 , então:
\(F=\ 9\ \cdot{10}^{9\ }\cdot\frac{\left|4\cdot{10}^{-6}\right|\ \cdot\left|-3\cdot{10}^{-6}\right|}{{(0,02)}^2}\)
\(F=\ 9\ \cdot{10}^{9\ }\cdot\frac{4\cdot{10}^{-6}\ \cdot3\cdot{10}^{-6}}{{(0,02)}^2}\)
\(F=\ 9\ \cdot{10}^{9\ }\cdot\frac{12\cdot{10}^{-6-6}\ }{0,0004}\)
\(F=\ 9\ \cdot{10}^{9\ }\cdot\frac{12\cdot{10}^{-12}\ }{0,0004}\)
\(F=\ \frac{9\cdot12\cdot{10}^{9-12}\ }{0,0004}\)
\(F=\ \frac{108\cdot{10}^{-3}\ }{0,0004}\)
\(F=\ 270\ 000\cdot{10}^{-3}\)
\(F=\ 270\cdot{10}^3\cdot{10}^{-3}\)
\(F=\ 270\cdot{10}^{3-3}\)
\(F=\ 270\cdot{10}^0\)
\(F=\ 270\cdot1\)
\(F=\ 270\ N\)
A força elétrica é atrativa porque as cargas possuem sinais contrários.
Resposta Questão 7
Letra E. Para resolver esse exercício, faremos uma comparação entre o valor da força elétrica final e a força elétrica inicial. Para isso, usaremos a fórmula da lei de Coulomb:
\(F=k\cdot\frac{\left|Q_1\right|\ \cdot\left|Q_2\right|}{d^2}\)
A força elétrica inicial mede:
\(F_{inicial}=k\cdot\frac{\left|Q_1\right|\cdot\left|Q_2\right|}{d_{inicial}^2}\)
\(F_{inicial}=k\cdot\frac{\left|q\right|\cdot\left|Q\right|}{d_{inicial}^2}\)
Em que Q=3q , então:
\(F_{inicial}=k\cdot\frac{\left|q\right|\cdot\left|3q\right|}{d_{inicial}^2}\)
\(F_{inicial}=k\cdot\frac{3\cdot q^2}{d_{inicial}^2}\)
Já a força elétrica final mede:
\(F_{final}=k\cdot\frac{\left|Q_1\right|\cdot\left|Q_2\right|}{d_{final}^2}\)
\(F_{final}=k\cdot\frac{\left|q\right|\cdot\left|Q\right|}{d_{final}^2}\)
\(F_{final}=k\cdot\frac{\left|q\right|\cdot\left|3q\right|}{d_{final}^2}\)
\(F_{final}=k\cdot\frac{3\cdot q^2}{d_{final}^2}\)
Como a distâncial final é metade da distância inicial, então:
\(F_{final}=k\cdot\frac{3\cdot q^2}{\left(\frac{d_{inicial}}{2}\right)^2}\)
\(F_{final}=k\cdot\frac{3\cdot q^2}{\frac{d_{inicial}^2}{4}}\)
\(F_{final}=k\cdot\frac{4\cdot3\cdot q^2}{d_{inicial}^2}\)
Contudo, \(F_{inicial}=k\cdot\frac{3\cdot q^2}{d_{inicial}^2}\), então, substituindo:
\(F_{final}=4\cdot F_{inicial}\)
A força final é quatro vezes a força inicial.
Resposta Questão 8
Letra B. Primeiramente, converteremos a distância de centímetros para metros:
\(80\ cm=0,8\ m\)
Calcularemos a carga elétrica por meio da fórmula da lei de Coulomb:
\(F=k\cdot\frac{\left|Q_1\right|\ \cdot\left|Q_2\right|}{d^2}\)
\(F=k\cdot\frac{\left|Q\right|\ \cdot\left|Q\right|}{d^2}\)
\(200=9\cdot{10}^9\cdot\frac{Q^2}{{0,8}^2}\)
\(200=9\cdot{10}^9\cdot\frac{Q^2}{0,64}\)
\(Q^2=\frac{200\cdot0,64}{9\cdot{10}^9}\)
\(Q^2=\frac{128}{9\cdot{10}^9}\)
\(Q^2\approx14,22\cdot{10}^{-9}\)
\(Q=\sqrt{14,22\cdot{10}^{-9}}\)
\(Q\approx\pm\ 1,192\cdot{10}^{-4}\ C\)
As duas cargas elétricas valem aproximadamente 1,192 ∙10-4 C , podendo ser ambas com sinal positivo ou com sinal negativo.
Resposta Questão 9
Alternativa C. Utilizando a fórmula da lei de Coulomb, faremos a comparação entre as forças final e inicial:
\(F=k\frac{\left|Q_1\right|\ \cdot\left|Q_2\right|}{d^2}\)
Isolamos a constante k na fórmulam, já que ela é a mesma no início e no final.
\(k=\ \frac{F\cdot d^2}{\left|Q_1\right|\ \cdot\left|Q_2\right|}\)
Portanto:
\(k_{inicial}=k_{final}\)
\(\frac{F_{inicial}\cdot d_{inicial}^2}{\left|q\right|\cdot\left|q\right|}=\frac{F_{final}\cdot d_{final}^2}{\left|q\right|\cdot\left|q\right|}\)
Eliminaremos as cargas elétricas, já que são iguais:
\(F_{inicial}\cdot d_{inicial}^2=F_{final}\cdot d_{final}^2\)
Como a força final é nove vezes a força inicial, temos:
\(F_{inicial}\cdot d_{inicial}^2={9\cdot F}_{inicial}\cdot d_{final}^2\)
Eliminando os termos semelhantes:
\(d_{inicial}^2=9\cdot d_{final}^2\)
Retirando a raíz quadrada em ambos os lados, obtemos:
\(d_{inicial}=3\cdot d_{final}\)
Resposta Questão 10
Letra E. De acordo com a fórmula da lei de Coulomb, é possível observar que o comportamento da força elétrica varia ao inverso do quadrado da distância.
Resposta Questão 11
Letra A. A fórmula da lei de Coulomb é dada como:
\(F=k\cdot\frac{\left|Q_1\right|\ \cdot\left|Q_2\right|}{d^2}\)
- F é a força de interação entre as partículas eletricamente carregadas, medida em Newton [N].
- Q1 e Q2 são os módulos das cargas das partículas, medidos em Coulomb [C] .
- d é a distância entre as cargas, medida em metros [m].
- k é a constante eletrostática do meio, medida em N∙m2/C2 .
Resposta Questão 12
Letra C. Abaixo, a correção em vermelho das alternativas incorretas:
I. Correta
II. Incorreta. A unidade de medida do campo elétrico é Coulomb por Newton.
III. Incorreta. A unidade de medida da força elétrica é Newton.
IV. Correta