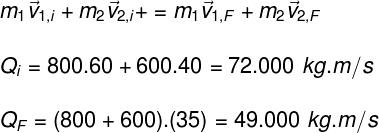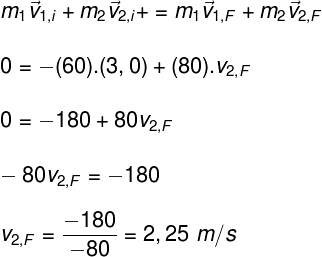Questão 1
Um corpo de 800 kg que se move a 60 m/s colide com a parte de trás de outro corpo de 600 kg que se move a 40 m/s, de forma que eles passam a mover-se juntos com velocidade de 35 m/s. Sobre essa colisão, assinale a alternativa correta:
a) A colisão é elástica e, portanto, a quantidade de movimento do conjunto de corpos não sofre alteração.
b) A energia cinética do sistema de corpos sofre um acréscimo após a colisão.
c) Trata-se de uma colisão não conservativa, na qual a quantidade de movimento do sistema é conservada em cerca de 49 000 kg.m/s.
d) Trata-se de uma colisão conservativa, na qual a quantidade de movimento do sistema é conservada em cerca de 49 000 kg.m/s.
e) Trata-se de uma colisão não conservativa, na qual a quantidade de movimento do sistema é reduzida em cerca de 23 000 kg.m/s.
Questão 2
Duas bolas de bilhar de massas iguais a 30,0 g cada, movendo-se uma em direção à outra com velocidade de 10 m/s, colidem, invertendo o sentido de movimento com a mesma velocidade. Sobre essa colisão, assinale a alternativa correta:
a) Parte da energia cinética do sistema é perdida durante a colisão, caracterizando-se, assim, como uma colisão inelástica.
b) A colisão referida é parcialmente inelástica, já que uma parte da quantidade de movimento do sistema é perdida.
c) A quantidade de movimento do sistema permanece constante, já que a colisão entre as bolas de bilhar é perfeitamente elástica.
d) A colisão referida no enunciado é perfeitamente inelástica.
e) A colisão referida no enunciado é parcialmente inelástica.
Questão 3
Um corpo A de massa 10,0 g move-se sobre uma superfície lisa e horizontal com velocidade de 4,0 m/s e colide com um corpo B de massa 20,0 g que se encontra em repouso. Após a colisão, o corpo A retrocede, movendo-se com velocidade de 1,0 m/s. A velocidade do corpo B em m/s, após a colisão, é igual a:
a) 2,5 m/s
b) 3,5 m/s
c) 4,0 m/s
d) 3,0 m/s
e) 2,0 m/s
Questão 4
Dois patinadores de massas iguais a 60,0 kg e 80,0 kg, inicialmente em repouso sobre uma pista de gelo lisa e livre de atritos, empurram-se mutuamente. O patinador de 60,0 kg move-se para a esquerda com velocidade de 3,0 m/s após o empurrão. Qual é a velocidade adquirida pelo segundo patinador?
a) 3,50 m/s
b) 3,25 m/s
c) 2,25 m/s
d) 0,65 m/s
e) 0,80 m/s
Resposta Questão 1
Letra E
Para determinarmos a conservação da quantidade de movimento, é necessário que a quantidade de movimento inicial de um sistema de corpos seja igual à quantidade de movimento final. Dessa forma, temos que:
![]()
Legenda:
Qi – quantidade de movimento inicial
QF – quantidade de movimento final
Como os dois veículos movem-se, inicialmente, no mesmo sentido, somamos as quantidades de movimento. Após a colisão, os dois veículos continuam movendo-se no mesmo sentido, porém com velocidades iguais. Dessa forma:
![]()
Legenda:
m1 – massa do corpo 1 (kg)
m2 – massa do corpo 2 (kg)
v1,i – velocidade inicial do corpo 1 (m/s)
v2,i – velocidade inicial do corpo 2 (m/s)
v1,F – velocidade final do corpo 1 (m/s)
v2,F – velocidade final do corpo 2 (m/s)
Substituindo os valores informados no enunciado do exercício, teremos a seguinte equação:
Observando os módulos das quantidades de movimento inicial e final desse sistema de corpos, vemos que não houve conservação, pois seu valor é diminuído após a colisão em cerca de 23 000 kg.m/s. Trata-se, portanto, de uma colisão não conservativa.
Resposta Questão 2
Letra C
Imediatamente antes da colisão, as bolas de bilhar movem-se em sentidos opostos e com velocidades iguais. Após a colisão, as bolas de bilhar mudam o sentido de movimento, mas continuam a mover-se com a mesma velocidade, de forma que a quantidade de movimento do sistema permanece constante.
Resposta Questão 3
Letra A
O exercício afirma que o corpo A move-se em uma superfície plana e livre de atritos, de forma que a colisão sofrida pelos corpos é uma colisão elástica. Portanto, podemos afirmar que a quantidade de movimento do sistema conserva-se:
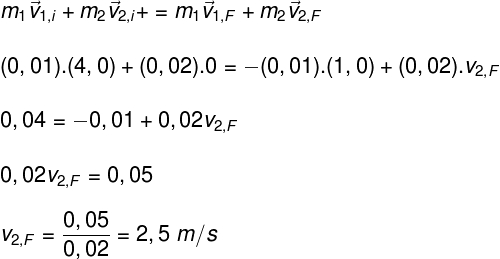
Resposta Questão 4
Letra C
Como a superfície em que se encontram os patinadores é lisa e livre de forças dissipativas, a quantidade de movimento inicial do sistema é igual à quantidade de movimento final. Dessa forma:
Inicialmente, os patinadores encontravam-se em repouso, logo, a quantidade de movimento inicial do sistema é nula (igual a zero). Fazendo o cálculo, encontramos que o segundo patinador, de massa 80,0 kg, irá mover-se com velocidade de 2,25 m/s.