Questão 1
(PUC) Num bairro onde todos os quarteirões são quadrados e as ruas paralelas distam 100 m uma da outra, um transeunte faz o percurso de P a Q pela trajetória representada no esquema:
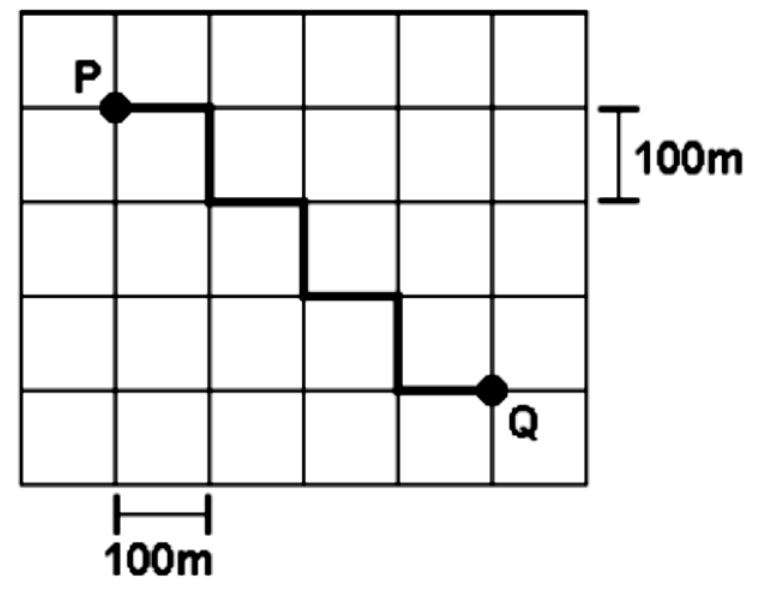
O deslocamento vetorial desse transeunte tem módulo, e metros, igual a:
A) 300
B) 350
C) 400
D) 500
E) 700
Questão 2
(Mackenzie) Um corpo é atirado verticalmente para cima a partir do solo com velocidade inicial de módulo 50 m/s. O módulo de sua velocidade vetorial média entre o instante de lançamento e o instante em que retorna ao solo é:
A) 50 m/s
B) 25 m/s
C) 5,0 m/s
D) 2,5 m/s
E) zero
Questão 3
(PUC) Você e seu amigo resolvem ir ao último andar de um edifício. Vocês partem juntos do primeiro andar. Entretanto, você vai pelas escadas e seu amigo, pelo elevador. Depois de se encontrarem na porta do elevador, descem juntos pelo elevador até o primeiro andar. É correto afirmar que:
A) o seu deslocamento foi maior que o de seu amigo.
B) o deslocamento foi igual para você e para seu amigo.
C) o deslocamento de seu amigo foi maior que o seu.
D) a distância que seu amigo percorreu foi maior que a sua.
Questão 4
(Mackenzie) Um avião, após deslocar-se 120 km para nordeste (NE), desloca-se 160 km para sudeste (SE). Sendo um quarto de hora o tempo total dessa viagem, o módulo da velocidade vetorial média do avião, nesse tempo, foi de
A) 320 km/h
B) 480 km/h
C) 540 km/h
D) 640 km/h
E) 800 km/h
Questão 5
Sabendo que uma partícula está inicialmente na posição \((1\ m)\hat{i}+(2\ m)\hat{j}+(3\ m)\hat{k}\) e depois passa para a posição \((2\ m)\hat{i}+(4\ m)\hat{j}+(6\ m)\hat{k}\), calcule o seu deslocamento.
A) \((1\ m)\hat{i}+(2\ m)\hat{j}+(3\ m)\hat{k}\)
B) \((2\ m)\hat{i}+(4\ m)\hat{j}+(6\ m)\hat{k}\)
C) \((1\ m)\hat{i}+(2\ m)\hat{j}+(4\ m)\hat{k}\)
D) \((2\ m)\hat{i}+(4\ m)\hat{j}+(10\ m)\hat{k}\)
E) \((1\ m)\hat{i}+(4\ m)\hat{j}+(5\ m)\hat{k}\)
Questão 6
Determine a velocidade média de uma partícula que teve um deslocamento de \((15\ m)\hat{i}+(-6\ m)\hat{j}+(-3\ m)\hat{k}\) no instante t=3 s
.
A) \((2\ m/s)\hat{i}+(-1\ m/s)\hat{j}+(0,2\ m/s)\hat{k}\)
B) \((5\ m/s)\hat{i}+(-2\ m/s)\hat{j}+(1\ m/s)\hat{k}\)
C) \((7\ m/s)\hat{i}+(2\ m/s)\hat{j}+(0,3\ m/s)\hat{k}\)
D) \((10\ m/s)\hat{i}+(3\ m/s)\hat{j}+(1\ m/s)\hat{k}\)
E) \((12\ m/s)\hat{i}+(-2\ m/s)\hat{j}+(0,4\ m/s)\hat{k}\)
Questão 7
Calcule a aceleração média de uma partícula que se desloca em uma velocidade de \((-2\ m/s)\hat{i}+(1\ m/s)\hat{j}+(9\ m/s)\hat{k}\) no instante t=2 s.
A) \((2\ m/s^2)\hat{i}+(-2\ m/s^2)\hat{j}+(-3,5\ m/s^2)\hat{k}\)
B) \((1\ m/s^2)\hat{i}+(-1\ m/s^2)\hat{j}+(-2,5\ m/s^2)\hat{k}\)
C) \((-1\ m/s^2)\hat{i}+(0,5\ m/s^2)\hat{j}+(1,5\ m/s^2)\hat{k}\)
D) \((-2\ m/s^2)\hat{i}+(1\ m/s^2)\hat{j}+(2,5\ m/s^2)\hat{k}\)
E) \((-3\ m/s^2)\hat{i}+(2\ m/s^2)\hat{j}+(3,5\ m/s^2)\hat{k}\)
Questão 8
Um automóvel partiu da posição (1,0, 0)
em direção à posição (0,2,-1). Com base nessas informações, qual foi o módulo do seu deslocamento?
A) \(\sqrt3\ m\)
B) \(2\ m \)
C) \(\sqrt5\ m\)
D) \(\sqrt6\ m\)
E) \(3\ m\)
Questão 9
Dê o módulo da velocidade de um automóvel que se desloca numa velocidade igual a \((-3\ m/s)\hat{i}+(0\ m/s)\hat{j}+(4\ m/s)\hat{k}\).
A) 1 m/s
B) 2 m/s
C) 3 m/s
D) 4 m/s
E) 5 m/s
Questão 10
Durante 1 minuto, um móvel altera a sua velocidade de \((-2\ m/s)\hat{i}+(3\ m/s)\hat{j}+(1\ m/s)\hat{k}\) para\((-1m/s)\hat{i}+(0,5\ m/s)\hat{j}+(3\ m/s)\hat{k}\). Com base nessas informações, calcule a sua aceleração média nesse intervalo de tempo.
A) \(\left(\frac{1}{60}\ m/s^2\right)\ \hat{i}+\left(-\frac{0,5}{12}\ m/s^2\right)\hat{j}+\left(\frac{1}{30}\ m/s^2\right)\hat{k}\)
B) \( \left(\frac{1}{50}\ m/s^2\right)\ \hat{i}+\left(-2\ m/s^2\right)\hat{j}+\left(\frac{1}{15}\ m/s^2\right)\hat{k}\)
C) \(\left(\frac{1}{40}\ m/s^2\right)\ \hat{i}+\left(-\frac{7}{12}\ m/s^2\right)\hat{j}+\left(-2\ m/s^2\right)\hat{k}\)
D) \(\left(\frac{1}{30}\ m/s^2\right)\ \hat{i}+\left(-3\ m/s^2\right)\hat{j}+\left(4\ m/s^2\right)\hat{k}\)
E) \(\left(\frac{1}{20}\ m/s^2\right)\ \hat{i}+\left(1\ m/s^2\right)\hat{j}+\left(\frac{1}{10}\ m/s^2\right)\hat{k}\)
Questão 11
Em relação à composição de movimentos estudados na cinemática vetorial, responda: quando os vetores de um corpo são oblíquos, o módulo do vetor resultante é calculado pela(o):
A) lei dos senos
B) lei dos cossenos
C) teorema de Pitágoras
D) adição de vetores
E) subtração de vetores
Questão 12
Analise as alternativas abaixo referentes às unidades de medida estudadas na cinemática vetorial:
I. O vetor deslocamento da partícula é medido em metros.
II. O vetor velocidade média é medido em metros por segundo ao quadrado.
III. O vetor aceleração média é medido em metros por segundo.
IV. O tempo é medido em segundos.
Está(ão) correta(s):
A) I e II.
B) III e IV.
C) I e III.
D) II e IV.
E) I e IV.
Resposta Questão 1
Alternativa D
Calcularemos o deslocalmento vetorial por meio do teorema de pitágoras:
\({hipotenusa}^2={{cateto}_1}^2+{{cateto}_2}^2\)
Desenhando um triângulo retângulo, em que a hipotenusa é a distância de P a Q, é possível observar que um dos catetos mede 3 quadrados e o outro cateto mede 4 quadrados. Como cada quadrado vale 100 m, então:
\(∆\vec{r}^2={{cateto}_1}^2+{{cateto}_2}^2\)
\(∆\vec{r}^2=\left(3\cdot100\right)^2+\left(4\cdot100\right)^2\)
\(∆\vec{r}^2={300}^2+{400}^2\)
\(∆\vec{r}^2=90.000+160.000\)
\(∆\vec{r}^2=250.000\)
\(∆\vec{r}=\sqrt{250.000}\)
\(∆\vec{r}=500\ m\)
Resposta Questão 2
Alternativa E
Como o corpo foi lançado e retornou para o mesmo ponto, o seu deslocamento é nulo, portanto, a sua velocidade média também é zero.
Resposta Questão 3
Alternativa B
Quando os amigos saíram do primeiro andar em direção ao último andar e depois retornaram ao primeiro andar, o deslocamento foi nulo, ainda que tenham ido por caminhos diferentes. Isso ocorre porque estamos somando e subtraindo vetores que têm mesma direção e sentidos opostos.
Resposta Questão 4
Alternativa E
Primeiramente, calcularemos o módulo do deslocamento do avião por meio do teorema de Pitágoras, em que a hipotenusa corresponde ao valor desse módulo:
\({hipotenusa}^2={{cateto}_1}^2+{{cateto}_2}^2\)
\(∆\vec{r}^2={120}^2+{160}^2\)
\(∆\vec{r}^2=14400+25.600\)
\(∆\vec{r}^2=40.000\)
\(∆\vec{r}=\sqrt{40.000}\)
\(∆\vec{r}=200\ km\)
Como ele levou ¼ de hora, então ocorreu durante 0,25 hora.
Por fim, calcularemos o módulo da velocidade vetorial média do avião por meio da sua fórmula:
\(\vec{v}_{média}=\frac{∆\vec{r}}{∆t}\)
\(\vec{v}_{média}=\frac{200}{0,25}\)
\(\vec{v}_{média}=800\ km/h\)
Resposta Questão 5
Alternativa A
Calcularemos o deslocamento da partícula por meio da sua fórmula:
\(∆ \vec{r}= \vec{r}f- \vec{r}i \)
\(∆\vec{r}=[(2\ m)\hat{i}+(4\ m)\hat{j}+(6\ m)]\hat{k} - [(1\ m)\hat{i}+(2\ m)\hat{j}+(3\ m)\hat{k}]\)
\(∆\vec{r}=[2\ -1]\hat{i}+[4\ -2]\hat{j}+[6\ -3]\hat{k}\)
\(∆\vec{r}=(1\ m)\hat{i}+(2\ m)\hat{j}+(3\ m)\hat{k}\)
Resposta Questão 6
Alternativa B
Calcularemos a velocidade média por meio da sua fórmula:
\(\vec{v}_{média}\frac{{\vec{r}}_f-{\vec{r}}_i}{t_f-t_i}\)
\(\vec{v}_{média}\frac{(15\ m)\hat{i}+(-6\ m)\hat{j}+(-3\ m)\hat{k}-0}{3-0}\)
\(\vec{v}_{média}\frac{(15\ m)\hat{i}+(-6\ m)\hat{j}+(-3\ m)\hat{k}}{3}\)
\(\vec{v}_{média}\left(5m/s\right)\hat{i}+\left(-2m/s\right)\hat{j}+\left(1m/s\right)\hat{k}\)
Resposta Questão 7
Alternativa C
Calcularemos a aceleração média por meio da sua fórmula:
\(\vec{a}_{média}\frac{{\vec{v}}_f-{\vec{v}}_i}{t_f-t_i}\)
\(\vec{a}_{média}\frac{(-2\ m/s)\hat{i}+(1\ m/s)\hat{j}+(3\ m/s)\hat{k}-0}{2-0}\)
\(\vec{a}_{média}\frac{(-2\ m/s)\hat{i}+(1\ m/s)\hat{j}+(3\ m/s)\hat{k}}{2}\)
\(\vec{a}_{média}\left(-1m/s^2\right)\hat{i}+\left(0,5m/s^2\right)\hat{j}+\left(1,5m/s^2\right)\hat{k}\)
Resposta Questão 8
Alternativa D
Primeriamente, calcularemos o deslocamento da partícula por meio da sua fórmula:
\(∆\vec{r}=\vec{r}f-\vec{r}i\)
\(∆\vec{r}=(0,2,-1)-(1,0,\ 0)\)
\(∆\vec{r}=(0-1)+(2-0)+(-1-0)\)
\(∆\vec{r}=(-1)î+(2)j+(-1)k\)
\(∆\vec{r}\left(-1,2,-1\right)\)
Depois, calcularemos o módulo do deslocamento pela raíz quadrada do quadrado das suas componentes, dada pela equação:
\(r=\sqrt{x^2+y^2+z^2}\)
\(r=\sqrt{{(-1)}^2+{(2)}^2+{(-1)}^2}\)
\(r=\sqrt{1+4+1}\)
\(r=\sqrt6\ m\)
Resposta Questão 9
Alternativa E
Calcularemos o módulo da velocidade por meio da raíz quadrada do quadrado das suas componentes, dada pela equação:
\(v=\sqrt{{v_x}^2+{v_y}^2+{v_z}^2}\)
\(v=\sqrt{{(-3)}^2+{(0)}^2+{(4)}^2}\)
\(v=\sqrt{9+0+16}\)
\(v=\sqrt{25}\)
\(v=5\ m/s\)
Resposta Questão 10
Alternativa A
Calcularemos a aceleração média por meio da sua fórmula:
\(\vec{a}_{média}=\frac{{\vec{v}}_f-{\vec{v}}_i}{t_f-t_i}\)
\(\vec{a}_{média}=\frac{\left[(-1m/s)\hat{i}+(0,5\ m/s)\hat{j}+(3\ m/s)\hat{k}\right]-\left[(-2\ m/s)\hat{i}+(3\ m/s)\hat{j}+(1\ m/s)\hat{k}\right]}{60-0}\)
\(\vec{a}_{média}=\frac{\left[-1-\left(-2\right)\right]\hat{i}+\left[0,5-3\right]\hat{j}+\left[3-1\right]\hat{k}}{60}\)
\(\vec{a}_{média}=\frac{(1\ m/s^2)\hat{i}+(-2,5\ m/s^2)\hat{j}+(2\ m/s^2)\hat{k}}{60}\)
\(\vec{a}_{média}=\left(\frac{1}{60}\ m/s^2\right)\ \hat{i}+\left(-\frac{0,5}{12}\ m/s^2\right)\hat{j}+\left(\frac{1}{30}\ m/s^2\right)\hat{k}\)
Resposta Questão 11
Alternativa B
Quando os vetores de um corpo são oblíquos, o módulo do vetor resultante é calculado pela lei dos cossenos e a sua orientação, pela regra do paralelogramo.
Resposta Questão 12
Alternativa E
I. O vetor deslocamento da partícula é medido em metros. (correta)
II. O vetor velocidade média é medido em metros por segundo ao quadrado. (incorreta)
O vetor velocidade média é medido em metros por segundo.
III. O vetor aceleração média é medido em metros por segundo. (incorreta)
O vetor aceleração média é medido em metros por segundo ao quadrado.
IV. O tempo é medido em segundos. (correta)
