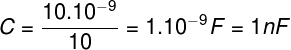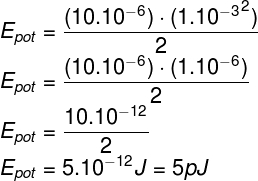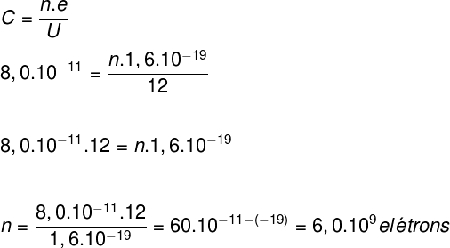Questão 1
Um capacitor acumula entre as suas placas uma quantidade de carga igual a 10 nC quando submetido a uma diferença de potencial de 10 V. Assinale a alternativa que apresenta corretamente a capacitância desse capacitor.
a) 1,0 nF
b) 10,0 nF
c) 1 pF
d) 100 nF
e)10 μF
Questão 2
A energia potencial armazenada entre as placas paralelas de um capacitor, cuja capacitância é de 10 μF, quando submetido a uma diferença de potencial de 1 mV, é equivalente a:
a) 10 nJ
b) 5pJ
c) 10 μJ
d) 10 mJ
e) 1 μJ
Questão 3
(PUC-MG) Se dobrarmos a carga acumulada nas placas de um capacitor, a diferença de potencial entre suas placas ficará:
a) inalterada.
b) multiplicada por quatro.
c) multiplicada por dois.
d) dividida por quatro.
e) dividida por dois.
Questão 4
(Uece) Um capacitor tem uma capacitância de 8,0 × 10-11 F. Se o potencial elétrico entre suas placas for 12 V, o número de elétrons em excesso na sua placa negativa é: (considere a carga de um elétron como e = 1,6 x 10-19C).
a) 9,6 × 1014
b) 8,0 ×1020
c) 6,0 × 109
d) 5,0 × 108
e) 11 x 107
Resposta Questão 1
Letra A
A capacitância, ou capacidade, de um capacitor pode ser calculada pela equação a seguir:
Q é a quantidade de carga (10 nC = 10.10-9C) armazenada entre os terminais do capacitor e U (10 V) é a diferença de potencial aplicada entre as placas desse capacitor. Dessa forma, temos que:
Resposta Questão 2
Letra B
Para calcular a energia potencial armazenada nas placas dos capacitores, podemos usar a equação a seguir:
De acordo com os dados informados pelo enunciado do exercício, a capacitância do dispositivo é de 10 μF (10.10-6 F), e a diferença de potencial entre suas placas é de 1 mV (1.10-3 V). Dessa forma, temos que:
Portanto, a energia potencial armazenada entre as placas do capacitor é de 5 pJ (5 picojoules).
Resposta Questão 3
Letra C
Como o capacitor permanecerá com a sua capacitância inalterada, ao dobrarmos a quantidade de cargas acumuladas em suas placas, deve-se dobrar o potencial entre elas, de modo que:
Logo, o seu potencial deverá ser multiplicado por dois.
Resposta Questão 4
Letra C
A capacitância de um capacitor é dada pela equação a seguir:
Além disso, a quantidade de cargas (Q) armazenada no capacitor é um múltiplo inteiro da carga fundamental do elétron, de acordo com a quantização da carga elétrica:
![]()
Dessa forma, após anotarmos os dados fornecidos pelo exercício, calcularemos o valor de n (o número de elétrons armazenados no capacitor):