Questão 1
(Vunesp) Num circuito elétrico, dois resistores, cujas resistências são R1 e R2, com R1 > R2 , estão ligados em série. Chamando de i1 e i2 as correntes que os atravessam e de V1 e V2 as tensões a que estão submetidos, respectivamente, pode-se afirmar que:
a) i1 = i2 e V1 = V2.
b) i1 = i2 e V1 > V2.
c) i1 > i2 e V1 = V2.
d) i1 > i2 e V1 < V2.
e) i1 < i2 e V1 > V2
Questão 2
(Unifenas) Dada a associação de resistores representada abaixo e sabendo-se que a diferença de potencial entre os pontos A e B é de 300 V, assinale a afirmação correta.
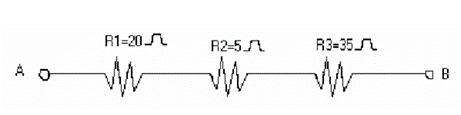
a) O resistor equivalente da associação é de 30 Ω
b) A intensidade da corrente elétrica na associação é de 10 A
c) A diferença de potencial no resistor R1 é de 200 V
d) A diferença de potencial no resistor R2 é de 50 V
e) A diferença de potencial no resistor R3 é de 175 V
Questão 3
Dois resistores, de mesma resistência elétrica de 0,5 Ω, de um circuito elétrico são ligados a uma tomada de 220 V. A partir dessas informações calcule a corrente elétrica que percorre esse sistema.
a) 220 A
b) 110 A
c) 55 A
d) 23 A
e) 11 A
Questão 4
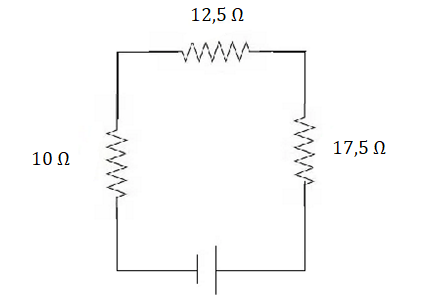
Calcule a resistência elétrica equivalente da associação em série a seguir:
a) 20 Ω
b) 40 Ω
c) 60 Ω
d) 80 Ω
e) 100 Ω
Questão 5
A associação de resistores em série apresenta diversas propriedades, a partir disso analise as alternativas abaixo:
I. Mesma corrente elétrica atravessando os resistores.
II. Diferentes valores de corrente elétrica atravessando os resistores.
III. Mesma ddp nos terminais de cada resistor.
IV. Diferentes valores de ddp nos terminais de cada resistor.
Quais alternativas estão corretas?
a) I e III.
b) II e IV
c) I e IV
d) II e III.
e) Todas estão corretas.
Questão 6
Determine a resistência elétrica equivalente de dois resistores de 10 Ω cada, associados em série.
a) 0 Ω
b) 5 Ω
c) 10 Ω
d) 15 Ω
e) 20 Ω
Questão 7
A associação de resistores em série é usada nas situações em que caso ocorra queima de algum dos resistores, todos os outros também queimem. Então, dentre as alternativas abaixo, em qual temos a aplicação de apenas associações de resistores em série?
a) Circuitos elétricos.
b) Lâmpadas públicas.
c) Celulares.
d) Pisca-pisca.
e) Lâmpadas residenciais.
Questão 8
Três resistores de resistência elétrica 8 Ω, 12 Ω e 16 Ω estão associados em série, então, a partir dessas informações, calcule a sua resistência elétrica equivalente.
a) 18 Ω
b) 36 Ω
c) 54 Ω
d) 72 Ω
e) 90 Ω
Questão 9
Considere um circuito elétrico contendo três resistores associados em série, de resistência elétrica 2 Ω, 5 Ω e 7 Ω. Calcule a corrente elétrica que os atravessa quando eles são conectados a uma bateria de 70 V.
a) 1 A
b) 3 A
c) 5 A
d) 7 A
e) 10 A
Questão 10
Um circuito elétrico possui 10 resistores elétricos associados em série. Sabendo que as resistências elétricas dos resistores vão de 1 Ω a 10 Ω, calcule a resistência elétrica equivalente dessa associação.
a) 10 Ω
b) 23 Ω
c) 46 Ω
d) 55 Ω
e) 100 V
Questão 11
Uma corrente elétrica de 4 A percorre dois resistores associados em série. Sabendo que a resistência elétrica dos resistores são 9 Ω e 11 Ω, determine a ddp em cada um desses resistores, respectivamente.
a) 36 V e 44 V
b) 18 V e 22 V
c) 44 V e 36 V
d) 22 V e 18 V
e) 9 V e 11 V
Questão 12
Analise as alternativas abaixo referentes às unidades de medida estudadas na associação de resistores em série:
I. A corrente elétrica é medida em Volt.
II. A tensão elétrica é medida em Ampere.
III. A resistência elétrica é medida em Ohm.
IV. A carga elétrica é medida em Coulomb.
V. A resistência elétrica equivalente é medida em Ohm.
Está(ão) correta(s):
a) I, II e III.
b) I, IV, V.
c) II, III, IV.
d) I, II,V
e) III, IV, V
Resposta Questão 1
LETRA B
Em uma associação de resistores em série, as correntes elétricas que percorrem os resistores são todas iguais, então i1 = i2. Já a ddp varia com a resistência elétrica de cada resistor, em que quanto maior a resistência elétrica, maior será a ddp, então V1 > V2.
Resposta Questão 2
LETRA E
Primeiramente, calcularemos a resistência elétrica equivalente dessa associação de resistores em série através da soma de todas as resistências elétricas:
\({R_{eq}=R}_1+R_2+R_3\)
\(R_{eq}=20+5+35\)
\(R_{eq}=60\ \mathrm{\Omega}\)
Depois, calcularemos a corrente elétrica através da fórmula da primeria lei de Ohm:
\(U=R\cdot i\)
\(300=60\cdot i\)
\(i=\frac{300}{60}\)
\(i=5\ A\)
Por fim, calcularemos a ddp nos terminais de cada resistor, através da fórmula da primeira lei de Ohm, então no resistor 1:
\(U_1=R_1\cdot i\)
\(U_1=20\cdot5\)
\(U_1=100\ V\)
No resistor 2, temos:
\(U_2=R_2\cdot iU_2=5\cdot5\)
\(U_2=25\ V\)
No resistor 3, temos:
\(U_3=R_3\cdot i\)
\(U_3=175\ V\)
Resposta Questão 3
LETRA A
Primeiramente, calcularemos a resistência elétrica equivalente da associação de resistores em série através da soma de todas as resistências elétricas:
\({R_{eq}=R}_1+R_2\)
\(R_{eq}=0,5+0,5\)
\(R_{eq}=1\ \mathrm{\Omega}\)
Por fim, calcularemos a corrente elétrica que atravessa os resistores através da fórmula da primeira lei de Ohm:
\(U=R\cdot i\)
\(220=1\cdot i\)
\(i=\frac{220}{1}\)
\(i=220\ A\)
Resposta Questão 4
LETRA B
Calcularemos a resistência elétrica equivalente da associação de resistores em série através da soma de todas as resistências elétricas:
\({R_{eq}=R}_1+R_2+R_3\)
\(R_{eq}=10+12,5+17,5\)
\(R_{eq}=40\ \mathrm{\Omega}\)
Resposta Questão 5
LETRA C
Na associação de resistores em série temos a passagem da mesma corrente em todos os resistores, contudo cada um deles apresenta um diferente valor de ddp em seus terminais.
Resposta Questão 6
LETRA A
Calcularemos a resistência elétrica equivalente da associação de resistores em série através da soma de todas as resistências elétricas:
\({R_{eq}=R}_1+R_2\)
\(R_{eq}=10+10\)
\(R_{eq}=20\ \mathrm{\Omega}\)
Resposta Questão 7
LETRA D
Os pisca-piscas são constituídos apenas de associação de resistores em série, assim, quando uma lâmpada queima, todas as demais também queimam.
Resposta Questão 8
LETRA B
Calcularemos a resistência elétrica equivalente da associação de resistores em série através da soma de todas as resistências elétricas:
\({R_{eq}=R}_1+R_2+R_3\)
\(R_{eq}=8+12+16\)
\(R_{eq}=36\ \mathrm{\Omega}\)
Resposta Questão 9
LETRA C
Primeiramente, calcularemos a resistência elétrica equivalente da associação de resistores em série através da soma de todas as resistências elétricas:
\({R_{eq}=R}_1+R_2+R_3\)
\(R_{eq}=2+5+7\)
\(R_{eq}=14\ \mathrm{\Omega}\)
Por fim, calcularemos a corrente elétrica que atravessa os resistores através da fórmula da primeira lei de Ohm:
\(U=R\cdot i\)
\(70=14\cdot i\)
\(i=\frac{70}{14}\)
\(i=5\ A\)
Resposta Questão 10
LETRA D
Calcularemos a resistência elétrica equivalente da associação de resistores em série através da soma de todas as resistências elétricas:
\({R_{eq}=R}_1+R_2+R_3+R_4+R_5+R_6+R_7+R_8+R_9+R_{10}\)
\(R_{eq}=1+2+3+4+5+6+7+8+9+10\)
\(R_{eq}=55\ \mathrm{\Omega}\)
Resposta Questão 11
LETRA A
Calcularemos a ddp nos terminais de cada resistor, através da fórmula da primeira lei de Ohm, então no resistor 1:
\(U_1=R_1\cdot i\)
\(U_1=9\cdot4\)
\(U_1=36\ V\)
No resistor 2, temos:
\(U_2=R_2\cdot iU_2=11\cdot4\)
\(U_2=44\ V\)
Resposta Questão 12
LETRA E
Abaixo vemos a correção em vermelho das alternativas incorretas.
I. Incorreta. A corrente elétrica é medida em Ampere.
II. Incorreta. A tensão elétrica é medida em Volt.
III. Correta.
IV. Correta.
V. Correta.
