Questão 1
Analise o copo a seguir:
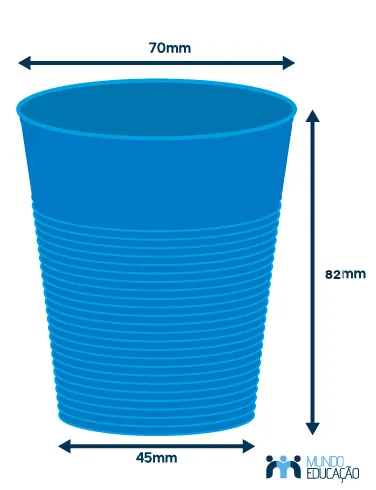
Utilizando π = 3, o volume desse copo é de, aproximadamente:
A) 100 ml
B) 150 ml
C) 200 ml
D) 250 ml
E) 300 ml
Questão 2
Um recipiente no formato de um tronco de cone possui altura de 12 cm, e raios medindo 15 cm e 25 cm. Utilizando π = 3,1, o volume desse recipiente é de:
A) 15.190 cm³
B) 14.280 cm³
C) 13.760 cm³
D) 12.990 cm³
E) 11.120 cm³
Questão 3
Um tronco de cone possui volume de 84π cm³. Sabendo que seus raios medem 6 cm e 3 cm, qual é a altura desse tronco de cone?
A) 3 cm
B) 4 cm
C) 5 cm
D) 6 cm
E) 7 cm
Questão 4
Um tronco de cone possui base maior com diâmetro de 10 cm e base menor com diâmetro de 6 cm. Se a altura for a média entre o comprimento dos diâmetros, o volume desse tronco de cone, em cm³, é de, aproximadamente:
A) 130,7π
B) 145,4π
C) 150π
D) 152,3π
E) 126,6π
Questão 5
Uma piscina será construída no formato do tronco de um cone. A exigência é que ela tenha raio maior de 8 metros e raio menor de 5 metros. Qual deve ser a altura da piscina para que a sua capacidade seja de 232.200 litros?
(Use π=3.)
A) 1,5 metros
B) 1,7 metros
C) 1,8 metros
D) 1,9 metros
E) 2,0 metros
Questão 6
O volume de um tronco de cone é de 344,1 cm³. Sabendo que a sua altura é de 9 cm e o raio maior mede 4 cm, e ainda utilizando π = 3,1, a medida do raio menor é de:
A) 0,5 cm
B) 1 cm
C) 2 cm
D) 3 cm
Questão 7
Um tronco de cone possui volume igual a 4740 cm³. Sabendo que o raio da base maior é 14 cm e o raio da base menor é 6 cm, então qual é a altura desse tronco de cone?
(Use π = 3.)
A) 10 cm
B) 12 cm
C) 13 cm
D) 14 cm
E) 15 cm
Questão 8
David precisou informar à empresa o orçamento mensal gasto com água para manter o reservatório da dela sempre cheio. Sabe-se que, no primeiro dia de março, por exemplo, o reservatório estava cheio e que, a cada 7 dias, a empresa faz a troca da água, sendo que será gasto o valor de R$ 15 por metro cúbico utilizado no mês, mais uma taxa fixa de R$ 21 por mês. O reservatório possui formato do tronco de cone, sua altura é de 2 metros, o raio menor é de 2 metros, e o raio maior, de 3 metros. Utilizando π=3 , o valor gasto com água na manutenção da piscina é de:
A) R$ 2319
B) R$ 2493
C) R$ 2550
D) R$ 2624
E) R$ 2871
Questão 9
(Enem) Nas empresas em geral, são utilizados dois tipos de copos plásticos descartáveis, ambos com a forma de troncos de cones circulares retos:
• copos pequenos, para a ingestão de café: raios das bases iguais a 2,4 cm e 1,8 cm e altura igual a 3,6 cm;
• copos grandes, para a ingestão de água: raios das bases iguais a 3,6 cm e 2,4 cm e altura igual a 8,0 cm.
Uma dessas empresas resolve substituir os dois modelos de copos descartáveis, fornecendo para cada um de seus funcionários canecas com a forma de um cilindro circular reto de altura igual a 6 cm e raio da base de comprimento igual a y centímetros. Tais canecas serão usadas tanto para beber café como para beber água.
Sabe-se que o volume de um tronco de cone circular reto, cujos raios das bases são, respectivamente, iguais a R e r e a altura é h, é dado pela expressão:
\(V_{tronco\ de\ cone}=\frac{\pi h}{3}\cdot\left(R^2+r^2+Rr\right)\)
O raio y da base dessas canecas deve ser tal que y² seja, no mínimo, igual a
A) 2,664 cm.
B) 7,412 cm.
C) 12,160 cm.
D) 14,824 cm.
E) 19,840 cm.
Questão 10
(Ibade) O volume, em metros cúbicos, de um tronco de cone obtido a partir de um cone equilátero de raio igual a \(\sqrt3\) m, cortado na metade da altura, será:
A) \(\ \frac{3\pi}{8}\)
B) \(\frac{2\pi}{3}\)
C) \(\frac{21\pi}{8}\)
D) \(\frac{7\pi}{16}\)
E) \(\frac{3\pi}{16}\)
Questão 11
(Instituto Consulplan) Um cone circular reto tem o diâmetro da base medindo 12 cm e altura medindo 9 cm. Esse cone é interceptado por um plano β que é paralelo à base e está distante 6 cm do vértice. O volume do tronco de cone assim formado é:
(Use π=3,14.)
A) 76π cm³
B) 108π cm³
C) 238,64π cm³
D) 304π cm³
Questão 12
Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.
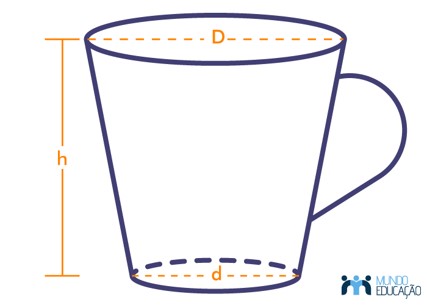
Sabe-se que 1 cm³ = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base). Qual é a capacidade volumétrica, em mililitro, dessa caneca?
(Utilize 3 como aproximação para π.)
A) 216
B) 408
C) 732
D) 2196
E) 2928
Resposta Questão 1
Alternativa C
O copo possui formato de tronco de cone. Retirando os dados:
h = 82 mm
r = 45 : 2 = 22,5
R = 70 : 2 = 35
Calculando o volume:
\(V=\frac{\pi h}{3}\cdot\left(R^2+Rr+r^2\right)\)
\(V=\frac{3\cdot82}{3}\cdot35²+35⋅22,5+22,52\)
\(V=82\cdot\left(1225+787,5+506,25\right)\)
\(V=82\cdot\left(1225+787,5+506,25\right)\)
\(V=82\cdot2518,75\ \)
\(V=206.537,5 mm³\)
Para transformar de mm para ml, basta dividir por 1000, então temos que:
206.537,5 : 1000 = 206,5375 ml
O volume desse copo é de aproximadamente 200 ml.
Resposta Questão 2
Alternativa A
Dados:
R = 25 cm
r = 15 cm
h = 12 cm
Calculando o volume do tronco de cone:
\(V=\frac{\pi h}{3}\cdot\left(R^2+Rr+r^2\right)\)
\(V=\frac{3,1\ \cdot\ 12}{3}\cdot\left({25}^2+25\cdot15+{15}^2\right)\)
\(V=3,1\cdot4\ \left(625+375+225\right)\)
\(V=12,4\cdot1225\)
\(V=15190\ cm³\)
Resposta Questão 3
Alternativa B
Sabemos que:
V = 84π cm³
R = 6 cm
r = 3 cm
Substituindo na fórmula:
\(V=\frac{\pi h}{3}\cdot\left(R^2+Rr+r^2\right)\)
\(84\pi=\frac{\pi h}{3}\cdot\left(6^2+6\cdot3+3^2\right)\)
\(84\pi=\frac{\pi h}{3}\cdot\left(36+18+9\right)\)
\(84\pi=\frac{\pi h}{3}\cdot63\)
\(84\pi=\frac{63\pi h}{3}\)
\(84\pi=21\pi h\)
\(\frac{84\pi}{21\pi}=h\)
\(h=4\ cm\)
Resposta Questão 4
Alternativa A
Calculando a altura do tronco de cone, temos que:
\(h=\frac{10+6}{2}=\frac{16}{2}=8\ cm\)
Agora temos que:
R = 10 : 2 = 5
r = 6 : 2 = 3
Calculando o volume:
\(V=\frac{\pi h}{3}\cdot\left(R^2+Rr+r^2\right)\)
\(V=\frac{\pi\cdot8}{3}\cdot\left(5^2+5\cdot3+3^2\right)\)
\(V=\frac{\pi\cdot8}{3}\cdot\left(25+15+9\right)\)
\(V=\frac{\pi\cdot8}{3}\cdot49\)
\(V=130,666...\ \pi\)
\(V=\ \cong130,7\pi\)
Resposta Questão 5
Alternativa C
Sabemos que V = 232.200 litros.
Para transformar de litros para metros cúbicos, dividiremos por 1000, logo, temos que:
V = 232.200 : 1000 = 232,2 m³
Conhecemos os valores dos raios, pois
R = 8 e r = 5
Calculando o volume:
\(V=\frac{\pi h}{3}\cdot\left(R^2+Rr+r^2\right)\)
\(232,2=\frac{3\cdot h}{3}\cdot\left(8^2+8\cdot5+5^2\right)\)
\(232,2=h\cdot\left(64+40+25\right)\)
\(232,2=h\cdot129\)
\(h=\frac{232,2}{129}\)
\(h=1,8\)
Resposta Questão 6
Alternativa D
Sabemos que o volume é de 344,1 cm³, além disso, foram dados:
h = 9
R = 4
π = 3,1
Substituindo na fórmula:
\(V=\frac{h\pi}{3}\cdot\left(R^2+Rr+r^2\right)\)
\(344,1=\frac{9\cdot3,1}{3}\cdot\left(4^2+4r+r^2\right)\)
\(344,1=3\cdot3,1\cdot\left(16+4r+r^2\right)\)
\(344,1=9,3\cdot\left(16+4r+r^2\right)\)
\(\frac{344,1}{9,3}=16+4r+r^2\)
\(37=16+4r+r^2\)
\(r^2+4r+16-37=0\)
\(r^2+4r-21=0\)
Resolvendo a equação do 2º grau, primeiro calcularemos o valor de Δ:
Dados:
a = 1
b = 4
c = -21
Então:
\(\Delta=b^2-4ac\)
\(\Delta=4^2-4\cdot1\cdot\left(-21\right)\)
\(\Delta=16+84\)
\(\Delta=100\)
Agora, pela fórmula de Bhaskara:
\(r=\frac{-b\pm\sqrt\Delta}{2a}\)
\(r=\frac{-4\pm\sqrt{100}}{2\cdot1}\)
\(r=\frac{-4\pm10}{2}\)
Como o valor procurado é uma medida, a única solução que faz sentido é a solução positiva.
\(r=\frac{-4+10}{2}=\frac{6}{2}=3\)
Então r = 3 cm.
Resposta Questão 7
Alternativa E
Sabemos que:
V = 4740
R = 14
r = 6
Logo, temos que:
\(V=\frac{\pi h}{3}\cdot\left(R^2+Rr+r^2\right)\)
\(4740=\frac{3\cdot h}{3}\cdot\left({14}^2+14\cdot6+6^2\right)\)
\(4740=h\cdot\left(196+84+36\right)\)
\(4740=h\cdot316\)
\(h=\frac{4740}{316}\)
\(h=15\)
Resposta Questão 8
Alternativa E
Primeiro vejamos qual é o volume do reservatório. Como ele possui formato de um tronco de cone, temos que:
\(V=\frac{\pi h}{3}\cdot\left(R^2+Rr+r^2\right)\)
\(V=\frac{3\cdot2}{3}\cdot\left(3^2+3\cdot2+2^2\right)\)
\(V=2\cdot\left(9+6+4\right)\)
\(V=2\cdot19\ \)
\(V=38\ m^3\)
Sabemos que no dia 1º esse reservatório estava cheio, então ele será preenchido de novo nos dias:
8, 15, 22 e 29, ou seja, 5 vezes.
Assim, o volume de água gasto em metros cúbicos foi de
\(5\cdot38=190\ m^3\)
O valor pago é de R$ 21 fixo mais R$ 15 por m³, então o gasto G é igual:
\(G=21+15\cdot190\ \)
\(G=21+2850\)
\(G=2871\ \)
O valor gasto é de R$ 2871.
Resposta Questão 9
Alternativa C
Queremos que a caneca seja usada para tomar tanto o café quanto a água, então, nesse caso, é necessário que ela tenha, no mínimo, o volume igual ao do copo maior.
Logo, o valor mínimo para y é tal que:
\(V_{copo\ maior}=V_{caneca}\)
Como o volume do copo maior é o volume de um tronco de cone, temos que:
\(V_{copo\ maior}=\frac{\pi h}{3}\cdot\left(R^2+r^2+Rr\right)\)
Por outro lado, a caneca possui formato de um cilindro, e o volume do cilindro é:
\(V_{caneca}=\pi r^2\cdot h\)
Então temos que:
\(\frac{\pi h_1}{3}\cdot\left(R^2+r^2+Rr\right)=\pi r^2\cdot h_2\)
Simplificando o π dos dois lados e substituindo as informações dadas para as medidas do copo maior e do cilindro, temos que:
\(\frac{8}{3}\left({3,6}^2+{2,4}^2+3,6\cdot2,4\right)=y^2\cdot6\)
\(\frac{8}{3}\left(12,96+5,76+8,64\right)=y^2\cdot6\)
\(\frac{8}{3}\cdot27,36=y^2\cdot6\)
\(72,96=y^2\cdot6\)
\(y^2=\frac{72,96}{6}\)
\(y^2=12,16\)
Então o valor mínimo que \(y^2\) pode admitir é 12,160 cm.
Resposta Questão 10
Alternativa C
Se o cone é equilátero, para calcular a altura dele, temos que:
\({\sqrt3}^2+h^2=\left(2\sqrt3\right)^2\)
\(3+h²=4⋅3\)
\(3+h²=12\)
\(h²=12-3\)
\(h²=9\)
\(h=\sqrt9\)
\(h=3\)
Sabendo que a altura do cone é 3, e que o tronco de cone foi cortado na metade, então a altura do cone é de 1,5.
Temos que:
\(R=\sqrt3\)
\(r=\frac{\sqrt3}{2}\)
\(h=\frac{3}{2}\)
Calculando o volume, temos que:
\(V=\frac{1}{3}\cdot\pi h\cdot\left(R^2+Rr+r^2\right)\)
\(V=\frac{1}{3}\cdot\frac{3\pi}{2}\cdot\left(\left(\sqrt3\right)^2+\sqrt3\cdot\frac{\sqrt3}{2}+\left(\frac{\sqrt3}{2}\right)^2\right)\)
\(V=\frac{\pi}{2}\cdot\left(3+\frac{3}{2}+\frac{3}{4}\right)\)
\(V=\frac{\pi}{2}\cdot\left(3+\frac{9}{4}\right)\)
\(V=\frac{\pi}{2}\cdot\left(\frac{12+9}{4}\right)\)
\(V=\frac{\pi}{2}\cdot\frac{21}{4}\)
\(V=\frac{21\pi}{8}\)
Resposta Questão 11
Alternativa C
A altura do tronco de cone é igual a
9 – 6 = 3 cm
Sabemos que 3 cm é igual a 2/3 da altura, então o diâmetro também será 2/3 do valor do diâmetro da base.
Assim:
\(D = 12 e d =\ \frac{2}{3}\cdot12 = \frac{24}{3} = 8\)
Logo, temos que:
R = 12 : 2 = 6
r = 8 : 2 = 3
h = 3
Então:
\(V=\frac{\pi h}{3}\cdot\left(R^2+Rr+r^2\right)\)
\(V=\frac{3\pi}{3}\cdot\left(6^2+6\cdot4+4^2\right)\)
\(V=\pi\cdot\left(36+24+16\right)\)
\(V=\pi\cdot76\)
\(V=3,14\cdot76\)
\(V=238,64 cm³\)
Resposta Questão 12
Alternativa C
Sabemos que:
D = 10, então o raio da circunferência maior é R = 10 : 2 = 5 cm.
d = 8, então o raio da circunferência menor é r = 8 : 2 = 4.
h = 12
Substituindo na fórmula:
\(V=\frac{\pi h}{3}\cdot\left(R^2+Rr+r^2\right)\)
\(V=\frac{3\cdot12}{3}\cdot\left(5^2+5\cdot4+4^2\right)\)
\(V=12\cdot\left(25+20+16\right)\)
\(V=12\cdot61\)
\(V=732\ cm³\)



