Questão 1
Dada uma função de R → R com a lei de formação f(x) = ax, em que a é um número positivo diferente de 1, julgue as afirmativas a seguir:
I → Essa função será crescente se a for positivo.
II → Se x = 0, então, f(x) = 1.
III → Essa é uma função exponencial.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
E) Todas as afirmativas são falsas.
Questão 2
Dada a função f(x) = 2x+3 + 10, o valor de x para que f(x) = 42 é de:
A) 2
B) 3
C) 4
D) 5
E) 6
Questão 3
Dada a função exponencial f(x) = (k – 4)x, sabendo que essa função é decrescente, o valor de k está entre:
A) 1 e 2
B) 2 e 3
C) 3 e 4
D) 4 e 5
E) 5 e 6
Questão 4
Um botânico, encantado com o pau-brasil, dedicou-se, durante anos de estudos, a conseguir criar uma função exponencial que medisse o crescimento dessa árvore no decorrer do tempo. Sua conclusão foi que, ao plantar-se essa árvore, seu crescimento, no decorrer dos anos, é dado por C(t) = 0,5 · 2t – 1. Analisando essa função, quanto tempo essa árvore leva para atingir a altura de 16 metros?
A) 7 anos
B) 6 anos
C) 5 anos
D) 4 anos
E) 3 anos
Questão 5
(Enem) Um trabalhador possui um cartão de crédito que, em determinado mês, apresenta o saldo devedor a pagar no vencimento do cartão, mas não contém parcelamentos a acrescentar em futuras faturas. Nesse mesmo mês, o trabalhador é demitido. Durante o período de desemprego, o trabalhador deixa de utilizar o cartão de crédito e também não tem como pagar as faturas, nem a atual nem as próximas, mesmo sabendo que, a cada mês, incidirão taxas de juros e encargos por conta do não pagamento da dívida. Ao conseguir um novo emprego, já completados 6 meses de não pagamento das faturas, o trabalhador procura renegociar sua dívida. O gráfico mostra a evolução do saldo devedor.
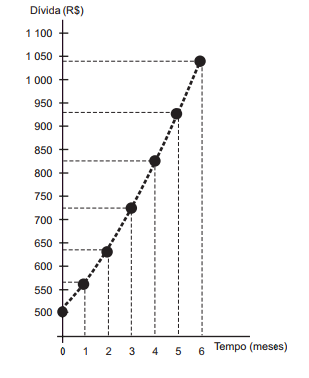
Com base no gráfico, podemos constatar que o saldo devedor inicial, a parcela mensal de juros e a taxa de juros são
A) R$ 500, constante e inferior a 10% ao mês.
B) R$ 560, variável e inferior a 10% ao mês.
C) R$ 500, variável e superior a 10% ao mês.
D) R$ 560, constante e superior a 10% ao mês.
E) R$ 500, variável e inferior a 10% ao mês
Questão 6
Quando uma matéria é radioativa, é comum que a sua massa se desintegre, no decorrer do tempo, de forma exponencial. O césio 137, por exemplo, possui meia-vida após 30 anos, ou seja, se havia, inicialmente, uma massa m0 de césio, após 30 anos, haverá metade de m0. Para descrever melhor essa situação, temos a função exponencial:
![]()
x→ quantidade de meias-vidas
m0 → massa inicial
f(x) → massa final
Pensando nisso, se houver 80 gramas de césio 137, inicialmente, após 150 anos, haverá um total de:
A) 2,0 gramas
B) 2,5 gramas
C) 3,0 gramas
D) 3,5 gramas
E) 5,0 gramas
Questão 7
O gráfico, a seguir, é a representação de uma função exponencial:
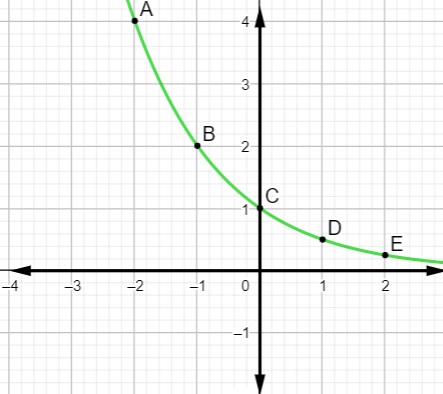
Analisando o gráfico, a lei de formação dessa função exponencial é:
A) f(x) = 5x
B) f(x) = 0,2x
C) f(x) = 2x
D) f(x) = 0,5x
E) f(x) = 0,5-x
Questão 8
O valor de um veículo vai diminuindo, no decorrer do tempo, por conta da depreciação, e essa redução ocorre de forma exponencial. Se um determinado veículo, que foi comprado por R$ 60.000, sofre desvalorizações de 10% do valor em relação ao ano anterior, ele custará R$ 39.366 após:
A) 2 anos
B) 3 anos
C) 4 anos
D) 5 anos
E) 6 anos
Questão 9
Ao observar, em um microscópio, uma cultura de bactérias, um cientista percebeu que elas se reproduzem como uma função exponencial. A lei de formação que relaciona a quantidade de bactéricas existentes com o tempo é igual a f(t) = Q · 2t-1, em que Q é a quantidade inicial de bactérias e t é o tempo em horas. Se nessa cultura havia, inicialmente, 700 bactérias, a quantidade de bactérias após 4 horas será de:
A) 7000
B) 8700
C) 15.300
D) 11.200
E) 5600
Questão 10
(Uneb-BA) A expressão P(t) = K · 20,05t fornece o número P de milhares de habitantes de uma cidade, em função do tempo t, em anos. Se, em 1990, essa cidade tinha 300.000 habitantes, quantos habitantes, aproximadamente, espera-se que ela tenha no ano 2000?
A) 352.000
B) 401.000
C) 423.000
D) 439.000
E) 441 000
Questão 11
(Enem 2015) O acréscimo de tecnologias no sistema produtivo industrial tem por objetivo reduzir custos e aumentar a produtividade. No primeiro ano de funcionamento, uma indústria fabricou 8000 unidades de um determinado produto. No ano seguinte, investiu em tecnologia adquirindo novas máquinas e aumentou a produção em 50%. Estima-se que esse aumento percentual se repita nos próximos anos, garantindo um crescimento anual de 50%. Considere P a quantidade anual de produtos fabricados no ano t de funcionamento da indústria. Se a estimativa for alcançada, qual é a expressão que determina o número de unidades produzidas P em função e t, para t ≥ 1?
A) P(t) = 0,5 . t-1 + 8000
B) P(t) = 50 . t-1 + 8000
C) P(t) = 4000 . t-1 + 8000
D) P(t) = 8000 . (0,5)t-1
E) P(t) = 8000 . (1,5)t-1
Questão 12
(Enem 2015) O sindicato de trabalhadores de uma empresa sugere que o piso salarial da classe seja de R$ 1800, propondo um aumento percentual fixo por cada ano dedicado ao trabalho. A expressão que corresponde à proposta salarial (s), em função do tempo de serviço (t), em anos, é s(t) = 1800 (1,03)t.
De acordo com a proposta do sindicato, o salário de um profissional de empresa com 2 anos de tempo de serviço será, em reais,
A) 7416,00.
B) 3819,24.
C) 3709,62.
D) 3708,00.
E) 1909,62.
Resposta Questão 1
Alternativa A
I → Falsa, para que a função seja crescente, não basta que a seja positivo, pois ele tem que ser maior que 1. Se a for um número entre 0 e 1, mesmo sendo positivo, a função será decrescente.
II → Verdadeiro, f(0) = a0 → todo número elevado a 0 é igual a 1.
III → Verdadeiro, na lei de formação da função, é possível ver que ela possui variável no expoente, característica essa da função exponencial.
Resposta Questão 2
Alternativa A
Dada a função f(x) = 2x+3 + 10, queremos encontrar o valor de x que faz com que f(x) = 42, para isso, igualamos a lei de formação da função a 42.
2x+3 + 10 = 42
2x+3 = 42 – 10
2x+3 = 32
Sabemos que 32 = 25:
2x+3 = 25
x + 3 = 5
x = 5 – 2
x = 2
Resposta Questão 3
Alternativa D
Para que a função seja decrescente, a sua base (k – 4) tem que ser menor que 1 e maior que 0.
Primeiro, verificaremos quando k – 4 será menor que 1.
k – 4 < 1
k < 1 + 4
k < 5
Agora, verificaremos quando k – 4 é maior que 0:
k – 4 > 0
k > 4
Sendo assim, o valor de k tem que estar entre 4 e 5 para que f(x) seja decrescente.
Resposta Questão 4
Alternativa B
Queremos encontrar o valor de t que faz com que C(t) = 16, então, temos que:
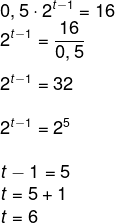
Resposta Questão 5
Alternativa C
Analisando a gráfico, é possível perceber que ele incia em R$ 500, pois, quando o tempo é igual a 0, a dívida é igual a 500.
Ao analisar o gráfico, é possível perceber que, a cada mês, o valor de juros é maior, o que faz com que a taxa seja variável.
Agora, para analisar se a taxa é superior ou inferior a 10%, sabemos que 10% de 500 = 50. Note que o crescimento no primeiro mês foi maior que 50 reais, logo, a taxa é superior a 10% ao mês.
Então, o valor inicial é de R$ 500 e a taxa é variável e superior a 10% ao mês.
Resposta Questão 6
Alternativa B
Sabemos que a meia-vida é de 30 anos, então, 150 : 30 = 5. Calculando f(5) e sabendo que m0 = 80, temos que:
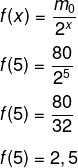
Resposta Questão 7
Alternativa D
Analisando o plano cartesiano, é possível perceber que o ponto (-1, 2) faz parte da função e que ela é uma função exponencial decrescente, então, temos que:
f(x) = ax
Por outro lado, temos que:
f(-1) = 2
Então:
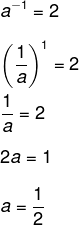
Sabemos que 1 : 2 = 0,5, então, a lei de formação dessa função é f(x) = 0,5x.
Resposta Questão 8
Alternativa C
Se o valor do veículo sempre diminui 10%, então, ele será 90% do valor anterior. Podemos descrever essa situação pela seguinte função exponencial
V(t) = 60.000 · 0,9t
Queremos encontrar o valor que faz com que V(t) = 39.366:
60.000 · 0,9t = 39.366
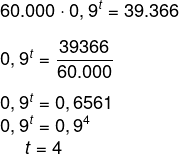
Resposta Questão 9
Alternativa E
Dados Q = 700 e t = 4, substituindo na fórmula:
f(t) = K · 2t-1
f(4) = 700 · 24-1
f(4) = 700 · 23
f(4) = 700 · 8
f(4) = 5600
Resposta Questão 10
Alternativa C
De 1990 até 2000, há 10 anos, então t = 10. Além disso K = 300.000, substituindo, temos que:
P(t) = K · 20,05t
P(10) = 300.000 · 20,05·10
P(10) = 300.000 · 20,5
P(10) = 300.000 · 1,41
P(10) = 423.000
Resposta Questão 11
Alternativa E
O número de unidades produzidas no primeiro mês é 8000.
P(1) = 8000
No segundo mês, há um aumento de 50%:
P(2) = 8000 · 1,5
No terceiro, há um novo aumento de 50% em relação ao mês anterior, ou seja:
P(3) = 8000 · 1,5 · 1,5 = 8000 · 1,5²
Note que esse comportamento é o mesmo sempre, logo, a lei de formação que descreve essa situação é:
P(t) = 8000 . (1,5)t-1
Resposta Questão 12
Alternativa E
Queremos encontrar o valor do salário para t = 2:
s(t) = 1800 (1,03)t
s(2) = 1800 (1,03)2
s(2) = 1800 · 1,0609
s(2) = 1909,62



