Questão 1
Existem vários tipos de função, sendo uma das classificações possíveis a de função injetora. Uma função é classificada como injetora quando
A) todo elemento do contradomínio é imagem de pelo menos um elemento no domínio.
B) elementos distintos do domínio sempre possuem imagens distintas no contradomínio.
C) ela é sobrejetora e bijetora.
D) admite uma função inversa, ou seja, se for inversível.
Questão 2
No diagrama a seguir, estão representadas duas funções: a função f e a função g.
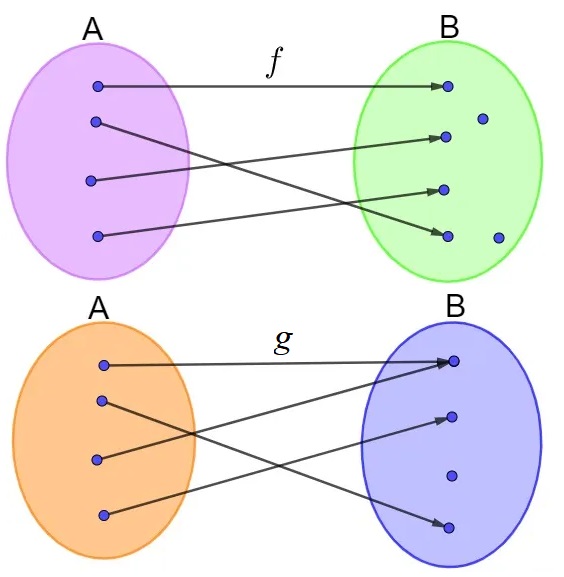
Analisando o diagrama, podemos afirmar que
A) a função f e a função g são injetoras.
B) a função f e a função g não são injetoras.
C) somente a função f é injetora.
D) somente a função g é injetora.
Questão 3
Uma função de f: A→ B possui lei de formação f(x) = x². Analisando o contexto, podemos afirmar que
A) essa função nunca será injetora.
B) essa função será injetora se seu domínio for os números reais.
C) essa função será injetora se seu domínio for os números inteiros.
D) essa função será injetora se seu domínio for os números racionais.
E) essa função será injetora se seu domínio for os números naturais.
Questão 4
Dizemos que uma função é inversível se ela for bijetora, ou seja, sobrejetora e injetora ao mesmo tempo. A função é injetora sempre que dois elementos distintos de um domínio possuírem imagens distintas no contradomínio. A função é sobrejetora quando todos os elementos do domínio possuírem um único correspondente no contradomínio.
Então, dada a função f: A → B, em que A ={0, 1, 2, 3} e B{ – 2, – 1, 2, 7}, com lei de formação f(x) = x² – 2, podemos afirmar que
A) a função é inversível, pois ela é bijetora.
B) a função não é inversível, pois ela é injetora, mas não sobrejetora.
C) a função não é inversível, pois ela é sobrejetora, mas não injetora.
D) a função não é inversível, pois ela é bijetora.
Questão 5
Dada a função f: A → B, em que A = {-2, 0, 1, 2} e B = {0, 1, 4}, com lei de formação f(x)= x², podemos afirmar que
A) essa função é injetora, pois satisfaz a sua definição teórica.
B) essa função não é sobrejetora, porque f(1) ≠ f(2).
C) essa função é constante, porque f( – 2) = f(2).
D) essa função é exponencial, devido à sua lei de formação.
E) essa função não é injetora, pois f( – 2) = f (2).
Questão 6
Sobre as funções, julgue as afirmativas a seguir:
I → Toda função é injetora.
II → Toda função injetora é inversível.
III → Toda função bijetora é injetora.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Todas as afirmativas são falsas.
Questão 7
A seguir está representado o gráfico da função f(x) = x³ – 2x, com domínio e contradomínio no conjunto dos números reais.
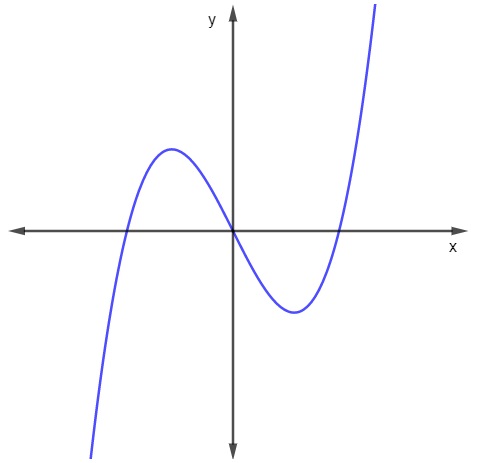
Analisando o gráfico da função, marque a alternativa correta:
A) Essa função é uma função exponencial.
B) Essa função é uma função bijetora.
C) Essa função não é uma função injetora.
D) Essa função é uma função composta.
E) Essa função não é uma função polinomial.
Questão 8
O gráfico a seguir é a representação do gráfico de uma função exponencial.
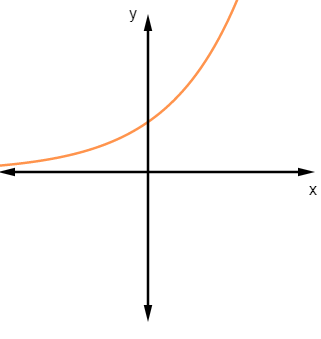
Analisando o gráfico acima, podemos afirmar que para esse intervalo essa função é
A) ímpar.
B) par.
C) injetora.
D) sobrejetora.
E) quadrática.
Questão 9
Analisando a função de lei de formação f(x) = |3x + 2|, com domínio e contradomínio nos números reais, julgue as afirmativas a seguir:
I → Essa função é injetora.
II → f(1) = f( – 1).
III → A imagem dessa função são os números reais positivos.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Todas as afirmativas são falsas.
Questão 10
Analisando a função f(x) = 3x – 4, com domínio e contradomínio nos números reais, podemos afirmar que
A) se trata de uma função do 2º grau.
B) se trata de uma função injetora.
C) f(20) = 64.
D) se trata de uma função linear.
Questão 11
Sendo f: A → B uma função cuja lei de formação é f(x,y) = x – y, dados os conjuntos A = {(1,2); (1,1); (2,1); (5,3)} e B = { – 1, 0, 1, 2, 3}, podemos classificar essa função como
A) afim.
B) injetora.
C) sobrejetora.
D) bijetora.
E) exponencial.
Questão 12
(Enem 2017 — PPL) No primeiro ano do Ensino Médio de uma escola, é hábito os alunos dançarem quadrilha na festa junina. Neste ano, há 12 meninas e 13 meninos na turma, e para a quadrilha foram formados 12 pares distintos, compostos por uma menina e um menino. Considere que as meninas sejam os elementos que compõem o conjunto A e os meninos, o conjunto B, de modo que os pares formados representem uma função f de A em B.
Com base nessas informações, a classificação do tipo de função que está presente nessa relação é
A) f é injetora, pois para cada menina pertencente ao conjunto A está associado um menino diferente pertencente ao conjunto B.
B) f é sobrejetora, pois cada par é formado por uma menina pertencente ao conjunto A e um menino pertencente ao conjunto B, sobrando um menino sem formar par.
C) f é injetora, pois duas meninas quaisquer pertencentes ao conjunto A formam par com um mesmo menino pertencente ao conjunto B, para envolver a totalidade de alunos da turma.
D) f é bijetora, pois dois meninos quaisquer pertencentes ao conjunto B formam par com uma mesma menina pertencente ao conjunto A.
E) f é sobrejetora, pois basta que uma menina do conjunto A forme par com dois meninos pertencentes ao conjunto B, assim nenhum menino ficará sem par.
Resposta Questão 1
Alternativa B
Por definição, a função é considerada injetora quando dois elementos distintos quaisquer do domínio da função são transformados pela função em elementos distintos do contradomínio.
Resposta Questão 2
Alternativa C
Analisando as funções, note que no primeiro caso, ou seja, na função f, elementos distintos do conjunto A possuem sempre imagem distintas no conjunto B. Não existe nenhum elemento do conjunto B que é imagem de dois ou mais elementos do conjunto A. Portanto, a função f é injetora.
Agora, analisando a função g, note que o primeiro elemento do conjunto B é imagem de dois elementos distintos do conjunto A. Sendo assim, a função não é injetora.
Conclui-se que somente a função f é injetora.
Resposta Questão 3
Alternativa E
Ao verificar as alternativas, nota-se que a função será injetora se o domínio for os números naturais, pois dados dois números naturais n e m distintos, sabemos que n² é sempre diferente de m².
Quando temos números inteiros, ao serem elevados ao quadrado, um número e o seu oposto geram resultados iguais. Logo, se o domínio for o conjunto dos racionais, dos reais ou dos inteiros, isso faz com que a função não seja injetora.
Resposta Questão 4
Alternativa A
Verificaremos se a função é injetora e sobrejetora.
Sua lei de formação é f(x) = x² – 2. Primeiramente, analisaremos se ela é injetora. Para isso, calcularemos o valor numérico da função para os valores do domínio A.
f(0) = 0² – 2 = – 2
f(1) = 1² – 2 = 1 – 2 = – 1
f(2) = 2² – 2 = 4 – 2 = 2
f(3) = 3² – 2 = 9 – 2 = 7
Note que elementos distintos possuem imagem distinta. Logo, a função é injetora.
É fácil perceber que a função é sobrejetora, pois 0, 1, 2 e 3 possuem correspondente no contradomínio. Sendo assim, essa função é injetora e sobrejetora, isto é, bijetora e inversível.
Resposta Questão 5
Alternativa E
Analisando a função, temos que: f( – 2) = ( – 2) ² = 4 e também que f(2) = 2² = 4. Sendo assim, essa função não é injetora, pois 2 e – 2, pertencentes ao domínio da função A, geram a mesma imagem no conjunto B, ou seja, f(2) = f( – 2).
Resposta Questão 6
Alternativa C
-
I → Falsa. Uma função pode ser injetora ou não.
-
II → Falsa. Uma função é inversível se ela for bijetora. Existem funções que são injetoras mas que não são bijetoras. Logo, nem toda função injetora é inversível.
-
III → Verdadeira. A função é bijetora se ela for injetora e sobrejetora. Assim, toda função bijetora é injetora.
Por fim, podemos afirmar que somente a afirmativa III é verdadeira.
Resposta Questão 7
Alternativa C
Analisando o gráfico da função, nota-se que há para uma mesma altura y mais de um correspondente. Dessa forma, valores diferentes da função possuem a mesma imagem, o que faz com que essa função não seja uma função injetora.
Resposta Questão 8
Alternativa C
Analisando o gráfico da função, é possível ver que elementos distintos no domínio sempre vão possuir imagens distintas no contradomínio. Isso quer dizer que um valor de y é correspondente de um único valor x.
Resposta Questão 9
Alternativa C
I → Falsa.
Sendo f(x) = k, temos:
|3x + 2| = k, se
3x + 2 = k ou 3x + 2 = – k.
Há dois valores distintos de x para f(x) = k, logo, elementos distintos possuem a mesma imagem, o que faz com que essa função não seja injetora.
II → Falsa.
f(x) = |3x + 2|
f(1) = |3 · 1 + 2| = |3 + 2| = |5| = 5
f( – 1) = |3( – 1) + 2| = | – 3 + 2| = | – 1| = 1
Conclui-se que f(1) ≠ f( – 1).
III → Verdadeira.
Sabemos que o módulo de um número qualquer é sempre positivo. Dessa forma, essa função terá como conjunto imagem o dos números reais positivos.
Resposta Questão 10
Alternativa B
A função f(x) = 3x – 4 é uma função injetora, pois satisfaz a definição, ou seja, elementos distintos do domínio possuem imagens distintas.
Resposta Questão 11
Alternativa B
Analisando a função, obtêm-se os seguintes cálculos:
f(1, 2) = 1 – 2 = – 1
f(1, 1) = 1 – 1 = 0
f(2, 1) = 2 – 1 = 1
f(5, 3) = 5 – 3 = 2
Ao comparar as imagens encontradas para cada elemento do domínio, é possível perceber que essa função satisfaz a definição de função injetora, pois elementos distintos possuem sempre imagens distintas. Portanto, podemos afirmar que essa função é injetora.
Resposta Questão 12
Alternativa A
Essa função é injetora, pois para cada elemento do conjunto A existe um único correspondente no conjunto B. Note que não há a possibilidade de duas meninas dançarem com o mesmo par, logo, essa relação é injetora.



